基于多项式的智能车换道轨迹规划
换道指的是车辆从一个车道变换到另一个车道的行为，常发生于平行车道之间或在高速路口等强制需要车辆汇入的地方。本文利用平行车道换道的场景来对多项式换道轨迹规划进行说明。
一、不考虑避障问题
图1为前方无障碍车辆且目标车道也没有障碍车辆时车辆换道的场景示意图。图中实线方框
表示换道车辆的当前位置，虚线方框
(符号中的下标0表示0号车，上标1表示第1时刻，也就是完成时刻，对应的上标0代表初始时刻，以下均同)表示换道车辆的目标位置。车自左向右行驶并完成换道到达位置。算法使用流程如下。
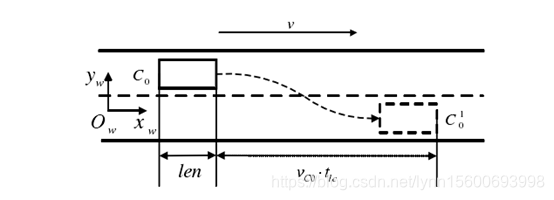
图1 前方无车辆且目标车道无车辆时车辆换道
1）建立车辆纵向、横向轨迹方程
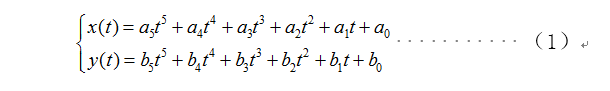
其中，x(t)为纵向轨迹方程，y(t)为横向轨迹方程。A=[a5,a4,a3,a2,a1,a0],B=[b5,b4,b3,b2,b1,b0]为多项式的系数。
2）求导
对x(t),y(t)分别求一阶和二阶导数，就可以得到纵向、横向的速度和加速度方程。
速度方程：
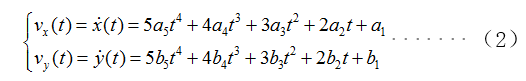
加速度方程：
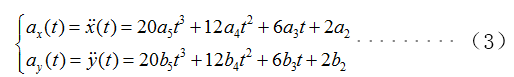
3）求解
假设车辆换道的初始状态和目标状态分别为:
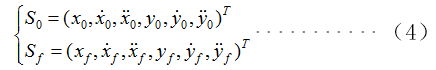
那么
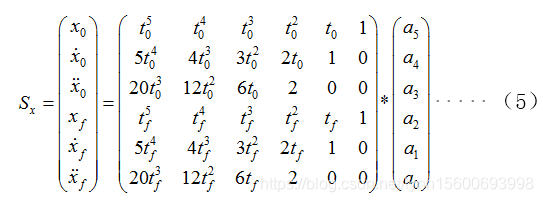
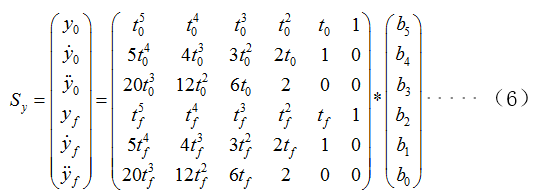
令
整理得
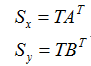
求解上式可得到行列式A，B的值，那么车辆行驶的横、纵向轨迹就可以确定。
二、考虑避障问题
若当前车道（如图2所示）或目标车道上有正在行驶的车辆，需要考虑车辆的避障问题。实际中，车辆行驶过程中纵向的速度和加速度的可变化范围比横向的可变化范围大，并且从驾驶舒适度来说，纵向的速度变化比横向的速度变化更容易接受，因此，多数学者均增加纵向(x方向)多项式次数的方法来实现避撞。在纵向采用六次多项式，横向还是采用五次多项式。
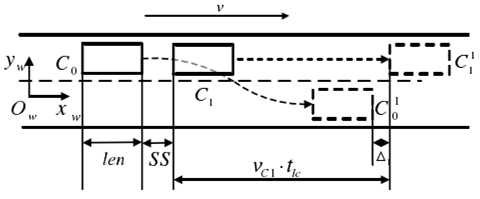
图2 前方有车辆但目标车道无车辆时车辆换道
1）建立车辆纵向、横向轨迹方程
将公式（1）修改为：
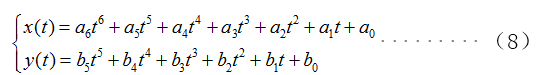
那么A*=[a6,a5,a4,a3,a2,a1,a0]
2）求导
只需求解公式（8）中纵向位移的一、二阶导数，如公式（9）所示。
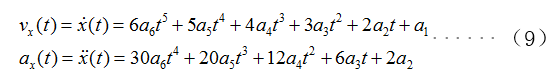
3）求解
车辆换道的初始状态和目标状态如（4）所示。
根据2）中的求导结果令
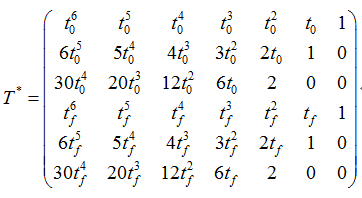
那么可以得到下式
公式（10）中含有13个未知量，然而通过初始和目标状态只能构造12个方程。学者们一般都是通过建立车辆避撞的方程来进行约束，然后求解公式（9）的系数。
三、补充说明
1）学者们在对换道的初始状态和目标状态进行赋值时通常做如下假设：
a 车辆沿车道中心线行驶
b 车辆纵向移动速度恒定
c 起始和终止时刻的横向速度、加速度均为0
那么，
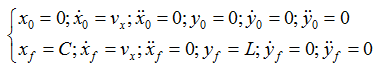
其中，L为车道宽度，可以参照国家公路标准，为已知量；Vx为车辆纵向的速度；C为车辆的纵向位移，可以利用车辆的纵向速度（Vx）乘以换道终止时间（tf）得到。由以上分析，利用五次多项式来进行换道轨迹规划时，难点就在于车辆纵向速度（Vx）和换道终止时间（tf）的选取。
一些学者们的做法是根据经验直接选值，这显然是不太合理的。因此，有些学者利用智能算法（如，遗传算法）、最优控制方法等并结合一些约束条件（如，避障约束）来对车辆纵向速度（Vx）和换道终止时间（tf）。如参考文献[2]、[3]。
2）因为多项式换道轨迹规划只需要知道车辆的初始状态和最终状态即可生成一条一阶导数和二阶导数都光滑的曲线，同时该轨迹也便于算法的扩展，能够实现车辆的避障处理和按照现实的行驶状况进行路线设计（如弯道换道）。因此，在无人车换道轨迹规划中，多项式轨迹规划的方法应用范围最广。
参考文献
[1] 谷广, "考虑驾驶特性的智能车辆协同换道轨迹规划," 硕士, 华南理工大学, 2018.
[2] 郑艳, 商雄, and 许龙, "基于多项式与遗传算法的智能车辆换道轨迹规划研究," in 第29届中国控制与决策会议, 中国重庆, 2017, p. 6.
[3] Y. Luo, Y. Xiang, K. Cao, and K. Li, "A dynamic automated lane change maneuver based on vehicle-to-vehicle communication," Transportation Research Part C-Emerging Technologies, vol. 62, pp. 87-102, Jan 2016.
本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！