c语言短除法求最大公约数的算法复杂度,两个求最大公约数C/C++算法实现

#include

#include

#include

using namespace std;

//求最大公约数 LCD(Largest Common Division)

//短除法

//m=8251, n=6105;

int LCD_ShortDiv(int m, int n) {

int i, time;

int f = 1; //相同因子的乘积

for(time=0; time<100000000; time++) {

for(i=2; i<=m&&i<=n; ) {

while(m%i==0&&n%i==0) {

f*=i; //将该因子与 前面的因子相乘

m/=i;

n/=i;

}

i++;

}

}

return f;

}

//辗转相除法(欧几里得算法)

int LCD_EucAlgorithm(int m, int n) {

int i, f, time;

for(time=0; time<100000000; time++) {

i = m % n; //取余数

while(i) {

m = n; //将小的n替换成m

n = i; //将余数i替换成n

i = m % n; //再次取余，直到i=0

}

//return n; //把最后除数返回

}

return n; //把最后除数返回

}

int main() {

int m=8251, n=6105;

int f1, f2;

clock_t start, finish;

double duration1, duration2;

start= clock();

f1 = LCD_ShortDiv(m, n);

finish=clock();

duration1=(double)(finish-start)/CLOCKS_PER_SEC;

//printf("time=%lf seconds\n",duration);

//printf("result=%d\n",f1);

cout << "LCD_ShortDiv用的时间为："<< duration1 <

cout << "最大公约数为："<< f1 <

start = clock();

f2 = LCD_EucAlgorithm(m, n);

finish = clock();

duration2 = (double)(finish-start) / CLOCKS_PER_SEC;

cout << "LCD_EucAlgorithm用的时间为："<< duration2 <

cout << "最大公约数为："<< f2 << endl << endl;

cout << "相差倍数:" << duration1 / duration2;

return 0;

}

证明过程如下：

想成分苹果

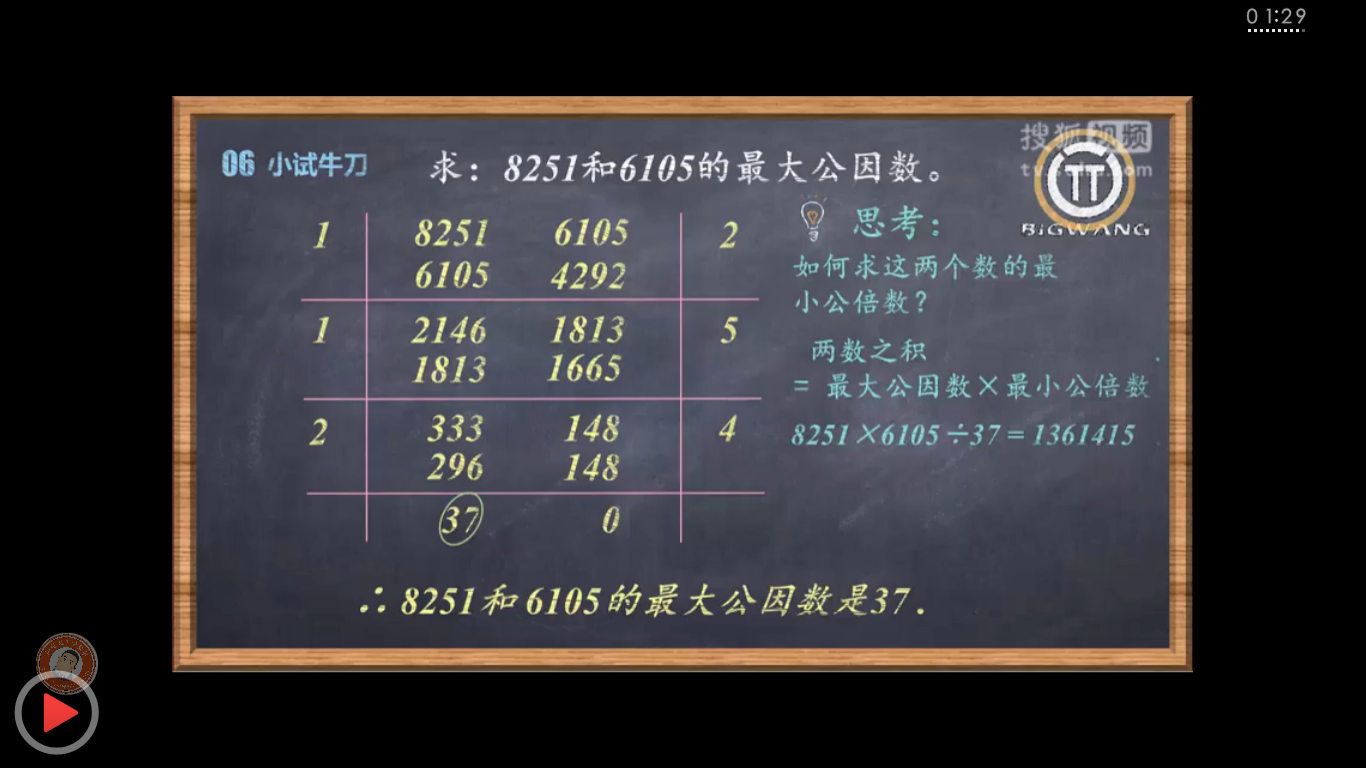
一个例题：

做题方法：

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！