二重积分1

目录

二重积分

 二重积分的性质

​编辑

中值定理

 二重积分的计算

方法1：利用直角坐标计算

 方法2：利用极坐标进行计算

 适用于极坐标的二重积分的特征

 对称性和奇偶性的应用

 题目

例题1：

 题目2：

 题目3：

 题目4：

 题目5：

  例题6：

  例题7：

 例题8：

 例题9：

 例题10：

 例题11：

 例题12：

二重积分

 二重积分的性质

 在相同的区域D上，当A函数始终小于等于B函数时，A函数在区域D的二重积分也小于等于g函数在区域D上的二重积分。

 在区域D上，多元函数f介于最小值与最大值之间，那么对应D区域上f的二重积分也介于最小值*面积与最大值*面积之间。

 绝对值的积分大于等于积分的绝对值。

中值定理

在区域D上存在一点，使得这一点对应的函数值与区域D的面积的乘积等于等于二重积分。

 二重积分的计算

方法1：利用直角坐标计算

做一条平行于y轴的线，与区域边界最多有两个交点。 

 方法2：利用极坐标进行计算

 适用于极坐标的二重积分的特征

 对称性和奇偶性的应用

 题目

例题1：

 题目2：

 题目3：

 题目4：

 题目5：

  例题6：

  例题7：

 例题8：

 例题9：

 例题10：

 例题11：

 例题12：

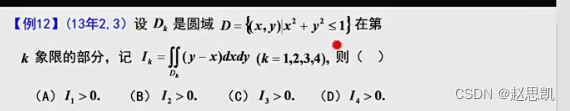
例题13：

目录

二重积分

 二重积分的性质

​编辑

中值定理

 二重积分的计算

方法1：利用直角坐标计算

 方法2：利用极坐标进行计算

 适用于极坐标的二重积分的特征

 对称性和奇偶性的应用

 题目

例题1：

 题目2：

 题目3：

 题目4：

 题目5：

  例题6：

  例题7：

 例题8：

 例题9：

 例题10：

 例题11：

 例题12：

例题13：

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！