排列组合C++实现方法（去重）

文章目录

• • 排列组合
  • 公式和定义
  • • 排列
    • 组合
  • 设计思路
  • 代码实现

排列组合

排列组合是组合学最基本的概念。所谓排列，就是指从给定个数的元素中取出指定个数的元素进行排序。组合则是指从给定个数的元素中仅仅取出指定个数的元素，不考虑排序。

公式和定义

排列

排列的定义：从n个不同元素中，任取m(m≤n,m与n均为自然数,下同）个不同的元素按照一定的顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列；从n个不同元素中取出m(m≤n）个元素的所有排列的个数，叫做从n个不同元素中取出m个元素的排列数，用符号 A(n,m）表示。注意：此外规定0! = 1。

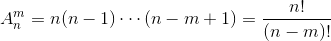
组合

组合的定义：从n个不同元素中，任取m(m≤n）个元素并成一组，叫做从n个不同元素中取出m个元素的一个组合；从n个不同元素中取出m(m≤n）个元素的所有组合的个数，叫做从n个不同元素中取出m个元素的组合数。用符号 C(n,m) 表示。C(n,m)=C(n,n-m）（n≥m)

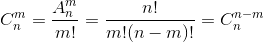
其他排列与组合公式 从n个元素中取出m个元素的循环排列数=A(n,m)/m=n!/m(n-m)!. n个元素被分成k类，每类的个数分别是n1,n2,…nk这n个元素的全排列数为 n!/(n1！×n2！×…×nk!). k类元素，每类的个数无限，从中取出m个元素的组合数为C(m+k-1,m）。

设计思路

• 组合：从n个数（可能有重复）中取出m个不同的数（这里数是指的元素），取出的数字中可能出现值相同的情况。如同在1，2，2，5中取到1，2，2和2，2，1；
• 组合的去重：1，2，2和2，2，1这两种组合对于排序来说就像是涂有两种颜色的两堆球，颜色1有一个，颜色2有两个。排序结果二者重复，所以在相同的组合里只留下一个用作排序；
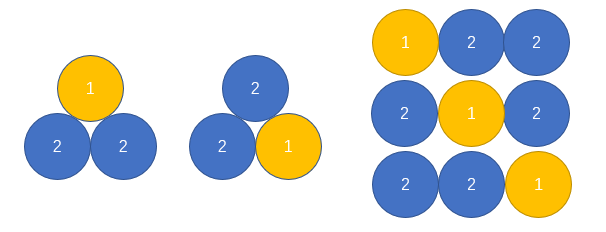
• 排列的去重：虽然在组合选择时已经进行了去重处理，但是包含重复的数字，也会导致遍历的时候产生重复序列，所以我们要对重复的排列序列进行排除，首先我们对数组进行排序，判断当前遍历到的数是否与前一个数相同，使用一个布尔型标记数组used来判断前一个相同的值是否被使用了，若正在被使用，说明正在处于前一个值得递归过程中，当前值不能被跳过；若没有被使用，说明这个值已经作为头部被使用过了，跳过当前值以排除重复。使用组合数组同类型的tmp来记录之前排列好的值，需要注意的是，遍历完成一个排列之后，需要还原tmp以进行下一次排列。
• 将所有组合的排列结果整合在一起，完成n个数（可能重复）中取m个不同数（这里的数是指元素）的排列组合。

代码实现

MyPerCom.h

#include
#include
#include
using namespace std;class MyPerCom
{
private:vector<vector<int>> m_pun;vector<vector<int>> m_com;vector<vector<int>> m_con;
public://回溯，无重复排列void Do_PermuteUnique(vector<int>& tmp, vector<bool>& used, vector<int>& nums) {if (tmp.size() == used.size()) { //结束标志m_pun.push_back(tmp);return;}for (int i = 0; i < used.size(); ++i) {// 剪枝条件：i > 0 是为了保证 nums[i - 1] 有意义// !used[i - 1] 是因为 nums[i - 1] 在深度优先遍历的过程中刚刚被撤销选择if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) //剪枝（除重）continue;if (!used[i]) {used[i] = true;tmp.push_back(nums[i]);Do_PermuteUnique(tmp, used, nums); //回溯探索used[i] = false;tmp.pop_back();}}}//排列vector<vector<int>> PermuteUnique(vector<int>& nums) {m_pun.clear();   //0if (nums.empty()) return m_pun;	//0(空)sort(nums.begin(), nums.end()); //排序使得重复字符相邻vector<int> tmp; //tmp.size()为0vector<bool> used(nums.size(), false);Do_PermuteUnique(tmp, used, nums); //回溯//Print_2D_Vector(m_res);return m_pun;}//二维打印template <typename T>void Print_2D_Vector(T& list) {for (int i = 0; i < list.size(); ++i) {for (int j = 0; j < list[i].size(); ++j)cout << list[i][j] << " ";cout << endl;}}//一维打印void Print_1D_Vector(vector<int>& list) {for (int i = 0; i < list.size(); ++i)cout << list[i] << " ";cout << endl;}//回溯，无重复组合void Do_Combination(vector<int>& a, vector<int>& b, int l, int m, int M) {//b用于临时存储结果。len(b)==M；l为左侧游标，初始值取0；M是取出个数；m用于指示深度，初始值取M）vector<int> c;int N = a.size();if (m == 0) {//for (auto i : b) {//	cout << i << ' ';//}//cout << endl;//Print_1D_Vector(b);c.clear();for (int i : b) {c.push_back(i);	}sort(c.begin(), c.end()); //存在相同重复数个数的某组数排序后相同，如1,2,2和2,2,1//cout << endl;if (!count(m_com.begin(), m_com.end(), c)) { //跳过重复的组合方式m_com.push_back(c);}return;}for (int i = l; i < N; ++i) {b[M - m] = a[i];Do_Combination(a, b, i + 1, m - 1, M);}}//组合vector<vector<int>> Combination(vector<int>& list, int& n) {m_com.clear();   //0if (list.empty()) return m_com;	//0(空)vector<int> a;a.assign(list.begin(), list.end()); //把list放在a里vector<int> b(n);Do_Combination(a, b, 0, n, n);//Print_2D_Vector(m_res);return m_com;}//无重复的排列组合结果vector<vector<int>> Permutation_Combination(vector<vector<int>>& list) {m_con.clear();vector<vector<int>> tmp;//Print_2D_Vector(list);for (int i = 0; i < list.size(); ++i) {//Print_1D_Vector(list[i]);tmp = PermuteUnique(list[i]);//cout << "_________________" <m_con.insert(end(m_con), begin(tmp), end(tmp)); //将每次排序后得到的结果添加到尾部}//Print_2D_Vector(m_con);return m_con;}
};

main.cpp

#include
#include
#include"MyPerCom.h"
typedef vector<int> vec;
using namespace std;vec Rand(int& m) { //生成有m个0~9随机数的数组int a = 0;	//a,b为随机区间int b = 9;vector<int> c;srand(time(0));//rand() % (b - a + 1) + afor (int i = 0; i < m; ++i) {c.push_back(rand() % (b - a + 1) + a);}return c;
}int main() {MyPerCom percom;int n,m;cout << "要进行排列组合的一组数的长度：";cin >> n;	//要进行排列组合的一组数的长度cout<< "排列组合需要取数的个数：";cin >> m ;	//需要取数的个数vec inpt = Rand(n);	//随机产生要排列组合的一组数//vec inpt{ 1,1,2,2,2 };//int n = 3;percom.Print_1D_Vector(inpt);vector<vec> a,b;if (m <= 0 || m > inpt.size() || inpt.empty()) {cout <<"输入的请要求组合数字个数为0或者输入有误"<<endl;return 0;}a = percom.Combination(inpt, m);b = percom.Permutation_Combination(a);	//排列组合percom.Print_2D_Vector(b);system("pause");return 0;
}

测试效果

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！