关于图的一些介绍。

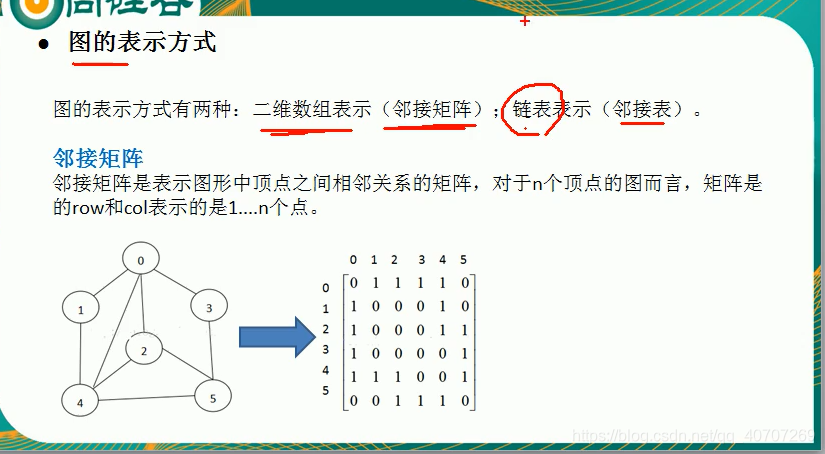
说变了，就是线性表和链表只有上线，下线没法违反监督上线，这一点很不好，我们需要的是上下线相互监督。

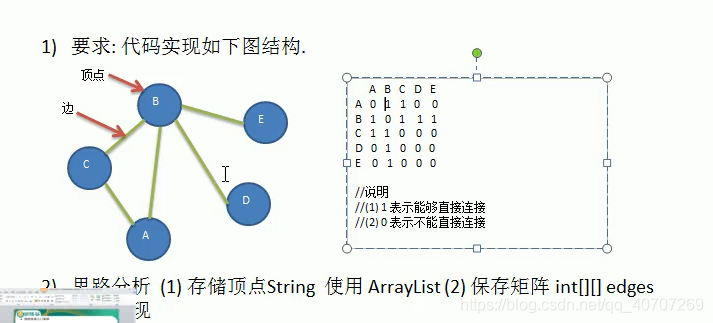
这种是无向图，互相之间都是联通的，A - B = 1 B - A = 1表示彼此都是联通的意思。

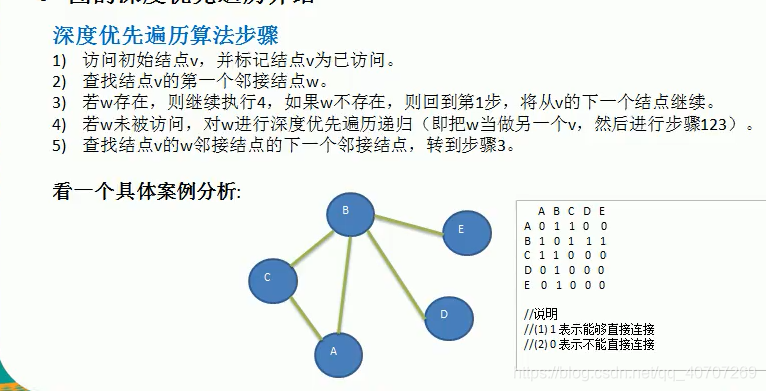
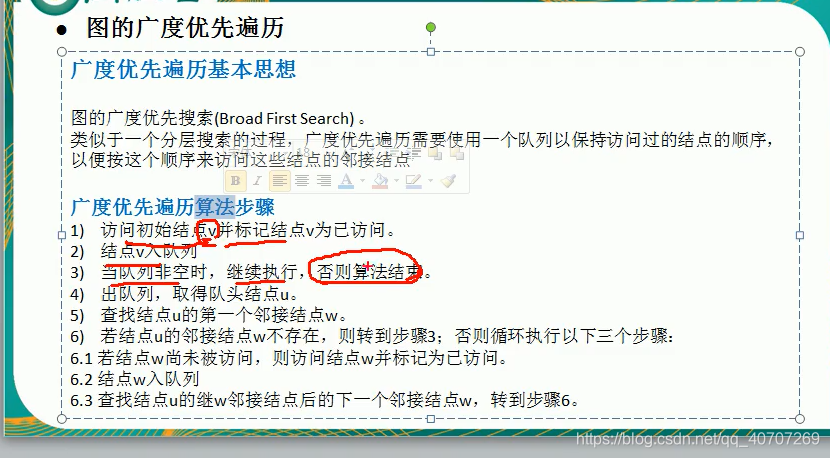
广度优先实在太傻逼了。就是取得一个节点的所有邻接节点，进去之后打印自己和所有邻接节点，然后将这些节点设置为访问过就行了。
然后将所有节点都送去执行上述操作（执行前先判断一下有没有被访问过，只要没被访问过就送去执行上述操作）

通过邻接矩阵方式实现深度优先广度优先题目写完了

package org.example.sort;import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;public class Graph {private ArrayList<String> vertexList;private int[][] edges;//记录矩阵private int numOfedes;//边的个数private boolean[] visited;//确定当前节点是否被访问过public static void main(String[] args) {//测试一把//先设置节点数量int n = 8;String[] Vertesx = {"a","b","c","d","e","f","g","h"};//设置顶点Graph graph = new Graph(n);for(String tex : Vertesx){graph.insert(tex);}//将顶点添加进图里//A - B A- c B - C B - D B - Egraph.insertedges(1,3,1);graph.insertedges(1,4,1);graph.insertedges(3,7,1);graph.insertedges(4,7,1);graph.insertedges(2,5,1);graph.insertedges(0,1,1);graph.insertedges(0,2,1);graph.insertedges(2,6,1);graph.insertedges(5,6,1);graph.show();System.out.println("");graph.dfs(0);System.out.println("广度");graph.bfs();}public Graph(int n){//初始化矩阵edges  = new int[n][n];vertexList = new ArrayList<>(n);numOfedes = 0;//初始化时候别忘记了这个记录访问节点的大小visited = new boolean[n];//随时创建这个变量的大小}//执行广度优先public void bfs(){for (int i = 0;i < getedgesNums();i++){if(!visited[i]){//只要没被访问过就去执行广度优先bfsNode(i);}}}//广度优先执行步骤private void bfsNode(int i){visited[i] = true;//进来就表示自己被访问了System.out.print(getValueOfIndex(i) + "-> ");//打印一把自己//广度优先遍历//先把当前节点所有的邻接表都访问了//需要一个队列来掌控这一切，队列把当前节点所有被访问过的子节点都一一入队//当所有子节点都被访问过之后，从队列里将所有子节点拿出来，递归进行访问，将每个子节点的子节点都访问过，每个节点都维持一个队列//保持掌控自己的子节点//先打印所有子节点for(Integer num : getAllNeighbor(i)){if(!visited[num]){System.out.print(getValueOfIndex(num) + "->");visited[num] = true;//设置已经访问过了}}}//根据索引获取当前节点所有的邻接节点public ArrayList<Integer> getAllNeighbor(int index){ArrayList<Integer> result = new ArrayList<>();for(int i = 0;i < getedgesNums();i++){if(edges[index][i] != 0){//说明联通result.add(i);}}return result;//将所有邻接点都整合到一起}//能进到遍历中说明这点;是可靠的public void dfs(int i){//每次传递进来的都是下标//深度优先进行遍历System.out.print(getValueOfIndex(i) + "->");//打印一下当前节点值visited[i] = true;//表示这个点已经遍历过了//打印完了看看有没有邻接点int next = getFirstNeighbor(i);//查找邻节点//这个点访问完成之后查找邻接点while (next != -1){//说明有邻接点if(!visited[next]){dfs(next);//邻节点没被访问，就去访问}//访问下一个邻接点，回溯回来就去访问下一个邻接点next = getNextNeighbor(i,next);//再找下一个邻接点，看看是不不是没访问过的}//说明有邻节点//直接遍历邻节}//获取第一个邻居下标//没有邻居会返回-1的public int getFirstNeighbor(int index){//获取到当前节点第一个邻居的下标//深度优先遍历用的//我将要查询的节点的下标给你，你遍历整个邻接矩阵表，遇到边为1的，就将列给返回，那个列下标，就是第一个我们邻接点for(int j = 0;j < vertexList.size();j++){if(edges[index][j] == 1){//找到了一个邻接点return j;//将这个邻节点索引返回去}}return -1;//整行遍历了一遍都没返回，说明没有邻接点，这时候返回-1说明没有邻接点}//获取一个节点第二个邻节点下标需要，当前节点下标，和上一个邻接点下标。public int getNextNeighbor(int index,int firstNeighbor){//index当前节点下标，first表示第一个邻节点下标，本身已经算是被使用过了。//获取当前节点，第二个邻接点下标//毕竟一个节点可能有好多个邻接点for(int j = firstNeighbor + 1;j < vertexList.size();j++){if(edges[index][j] == 1){return j;//返回第二邻接点下标}}return -1;//没有第二邻节点返回-1}//根据下标返回节点public String getValueOfIndex(int index){return vertexList.get(index);}public int getedgesNums(){//返回节点数量return  vertexList.size();//返回节点数量}//根据下标返回权值public int getWeight(int v1,int v2){return edges[v1][v2];}public void show(){//显示矩阵很简单直接遍历二维数组就行for(int[] link : edges){for(int temp : link){System.out.print(temp + " ");}System.out.println();}}public int getNumOfedes(){//返回边的数量//一条边代表一个联通return numOfedes;}public void insert(String vertex){vertexList.add(vertex);}public void insertedges(int v1,int v2,int weight){//记录矩阵//矩阵中有数值的下标用1表示//v1表示第一个顶点的下标，v2表示第二顶点的下标。edges[v1][v2] = weight;edges[v2][v1] = weight;numOfedes++;}}

邻接矩阵方式对图进行深度优先遍历有一些很有意思的方法

比如随机选择一个点进行切入
，切入后将上下左右所有可以访问的点都放进队列里，同时对这个点进行已经访问过处理（改为1,或者维持一个visited数组）
然后所有点就会进到链表尾巴
等待再次被重新
就是打击了你以后，记录一下你被打击了，然后把你的小弟扔进队列尾巴，一个个来等着被审判。

class Solution {public int numIslands(char[][] grid) {int count = 0;for(int i = 0; i < grid.length; i++) {for(int j = 0; j < grid[0].length; j++) {if(grid[i][j] == '1'){dfs(grid, i, j);count++;}}}return count;}private void dfs(char[][] grid, int i, int j){if(i < 0 || j < 0 || i >= grid.length || j >= grid[0].length || grid[i][j] == '0') return;grid[i][j] = '0';dfs(grid, i + 1, j);dfs(grid, i, j + 1);dfs(grid, i - 1, j);dfs(grid, i, j - 1);}
}

当然使用邻接表时候还要注意一下一个问题，就是一定要判断一下这个点越界不越级，越界点不行

有向图这样存储比较好。



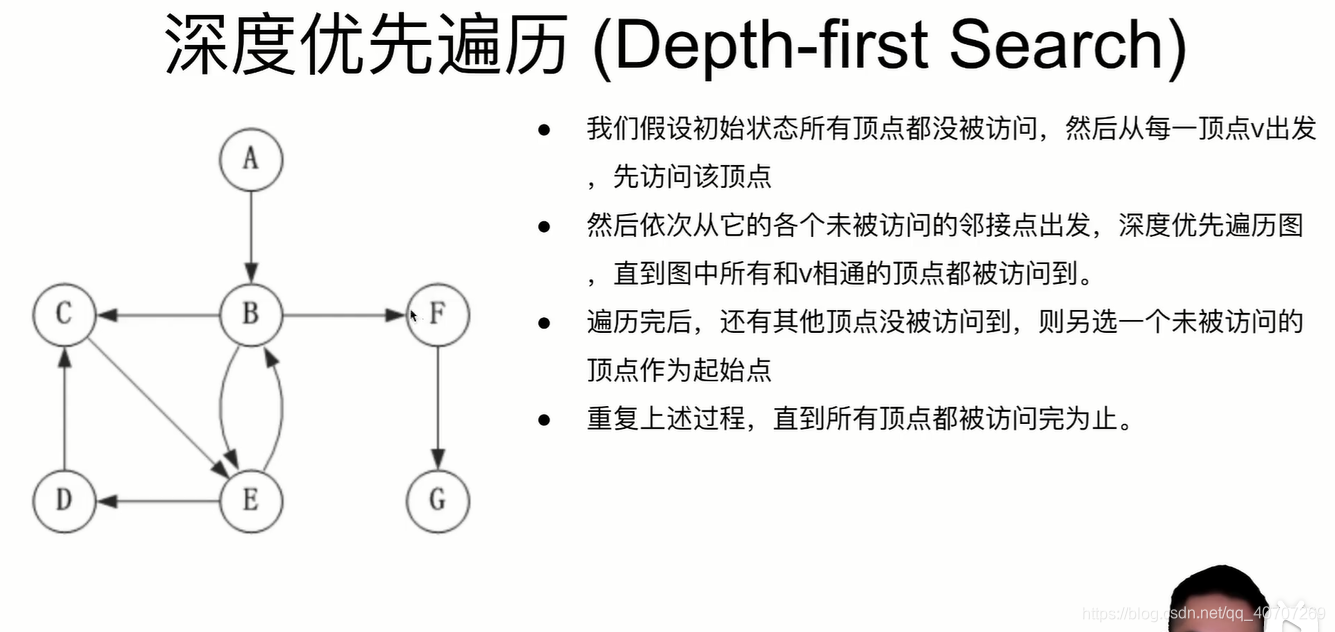
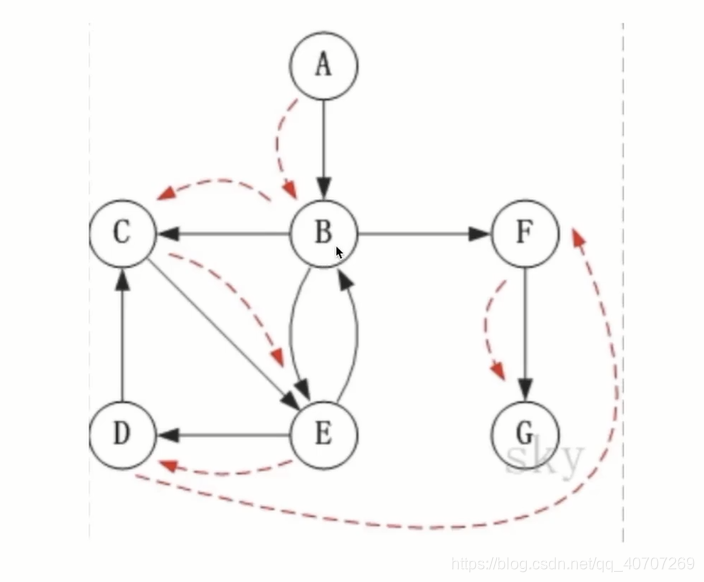
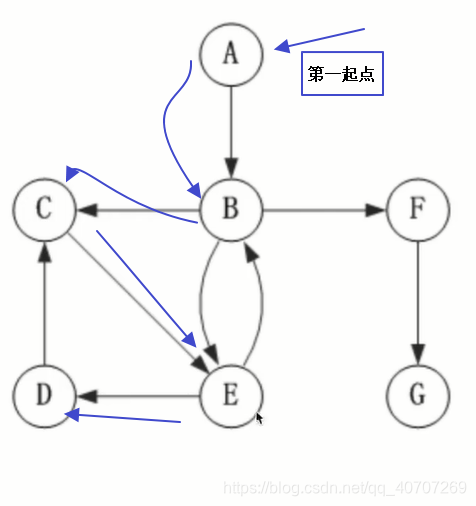
按照存储顺序，一个个访问节点，只要节点是按照存储顺序相连的，就进行一个个访问。
当遇到不相连的时候，就再找个节点作为第二起点

啥叫邻节点？就是按顺序走链表，当走到不能走的位置时候重新找一个起点。

广度优先遍历

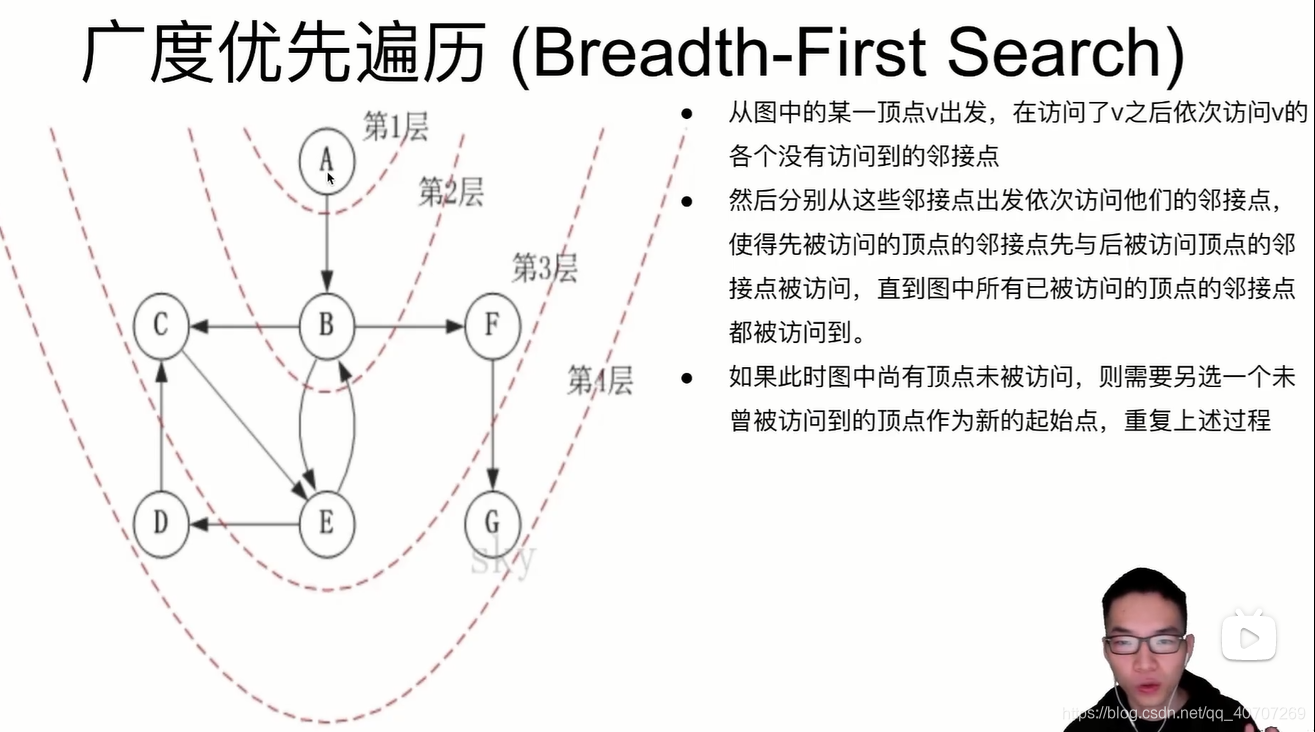
先把某一个结点的所有结点都给访问了，然后再访问，自己邻节点的所有邻结点。

说白了就是
深度优先，和狗熊掰棒子一样，不求学的扎实，就求学的深，先学的深入，然后再一点点补。就像读历史书一样，先把上下五千年都看了，知道上下五千年大概王朝更替是什么样子，然后，一朝代一朝代补历史。
广度优先就是说白了，先从秦朝开始看，看个几十本，把秦朝看的非常了解了，然后看汉朝，在看个几十本，再往下看。

深度优先就是进攻时候，不管后方敌人，大胆穿插，玩命往里面插，
穿插完了再回过来头扫清后方敌人。
广度优先就是先扫清前后左右一切障碍，然后再推进。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！