图像的典型特征描述子——LBP

以下文章摘录自：

《机器学习观止——核心原理与实践》

京东： https://item.jd.com/13166960.html

当当：http://product.dangdang.com/29218274.html

(由于博客系统问题，部分公式、图片和格式有可能存在显示问题，请参阅原书了解详情)

1.1    图像的典型特征描述子

1.1.1  LBP

LBP是Local Binary Patterns的缩写，即局部二值模式。它是由T. Ojala, M.Pietikäinen, 和 D. Harwood等人在1994年提出来的，属于一种特殊的纹理模型。

LBP描述子不仅计算过程相对简单，而且产生的最终效果也不错，因而在学术界和工业界的很多领域都得到了较为广泛的应用。例如目前非常火热的人脸识别研究方向中就有不少采用了这种描述子来完成的。另外，OpenCV和Scikit-image等多种图像处理库也专门提供了LBP的实现接口，其重要性可见一斑。

LBP算子除了原始版本，还有多个演进版本。

1.1.1.1          原始LBP算法

前者的主要计算步骤如下所示：

Step1. 将图像的被检测区域分割成一个个cells，例如16*16大小

Step2. 比较一个像素值与其周边8个neighbor的大小。换句话说，就是在一个3*3的区域中，最中间的像素值相比于其它像素的大小。如下图所示：

图 ‑ LBP中的阈值比较

Step3. 在上述比较过程中，如果某个neighbor的值比中间值小，那么它会被记为0;相反的就会被标注为1。这样一来3*3大小的框一共可以产生8个二进值(0或者1)的数值

Step4. 沿着正方向或者反方向来组装这8个二进制数，那么将得到一个新的数值。比如在上图所示的例子中，我们首先针对原始数据进行threshold处理，得到中间图;然后再采用顺时针方向来组成新数值，得到：

00010011 (二进制码)

=19 (十进制码)

最后我们把19赋予给中间的像素点，这样就完成了

如果用数学来表达的话，LBP的计算公式可以参考：

其中(xc, yc) 指的是3*3框中的中心点， ic和ip分别是中心点和它的各个neighbor的像素灰度值，而s则是如下所示的一个函数：

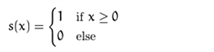
Step5. 重复以上步骤，直到处理完所有像素点，得到完整的LBP结果。

原始版本LBP的代码实现范例如下所示：

template <typename _Tp>

void lbp::OLBP_(const Mat& src, Mat& dst) {

    dst = Mat::zeros(src.rows-2, src.cols-2, CV_8UC1);

    for(int i=1;i

        for(int j=1;j

            _Tp center = src.at<_Tp>(i,j);

            unsigned char code = 0;

            code |= (src.at<_Tp>(i-1,j-1) > center) << 7;

            code |= (src.at<_Tp>(i-1,j) > center) << 6;

            code |= (src.at<_Tp>(i-1,j+1) > center) << 5;

            code |= (src.at<_Tp>(i,j+1) > center) << 4;

            code |= (src.at<_Tp>(i+1,j+1) > center) << 3;

            code |= (src.at<_Tp>(i+1,j) > center) << 2;

            code |= (src.at<_Tp>(i+1,j-1) > center) << 1;

            code |= (src.at<_Tp>(i,j-1) > center) << 0;

            dst.at(i-1,j-1) = code;

        }

    }

}

可以看到原始LBP的计算过程并不复杂。

1.1.1.2          圆形LBP算法

从前一小节可以看到，原始版本的LBP算法计算过程相当简单，而且可以较好的捕捉到图像的局部细节。不过它的一个主要缺点是覆盖范围不但是固定的，而且范围较小——这样一来在某些场景下并不能很好地满足不同尺寸和频率纹理的诉求。

为了克服上述的缺点，并达到灰度不变性等要求，LBP的作者又提出了一种名为圆形LBP算子(即Circular LBP或Extended LBP)的方法。后者不仅用圆形的邻域代替了3*3的正方形邻域，而且将范围也扩大到了半径为R的圆形中的P个像素点(其中R和P的具体取值都是可以设置的)。

根据R和P的取值不同，自然可以得到形态各异的LBP计算方式，如下示意图所示的分别是当R=1, 2, 3时的LBP情况：

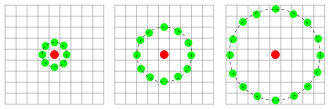
图 ‑ R和P取不同值时的圆形LBP算法

另外，利用可变半径的圆对近邻像素点进行编码，还可以得到不同的近邻表示方法。如下参考图所示：

图 ‑ 不同形态的近邻

假设中心点为(xc, yc)，那么在圆形LBP算法中neighbor点(xp, yp)的计算公式可以参考下面的表达式：

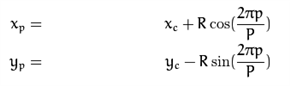
不难理解，通过上述计算公式得出的结果值有可能不在像素值的正常范围，此时可以考虑利用插值方式来解决。例如OpenCV采用的是bilinear interpolation，计算公式如下：

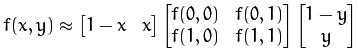
圆形LBP的参考实现代码如下所示：

void lbp::ELBP_(const Mat& src, Mat& dst, int radius, int neighbors) {

    neighbors = max(min(neighbors,31),1); // set bounds...

    dst = Mat::zeros(src.rows-2*radius, src.cols-2*radius, CV_32SC1);

    for(int n=0; n

        float x = static_cast(radius) * cos(2.0*M_PI*n/static_cast(neighbors));

        float y = static_cast(radius) * -sin(2.0*M_PI*n/static_cast(neighbors));

        // relative indices

        int fx = static_cast(floor(x));

        int fy = static_cast(floor(y));

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！