数据结构之B树/B+树
一、B树
1.B树的定义
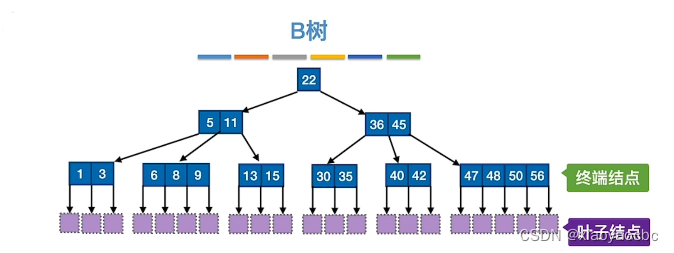
B树，又称多路平衡查找树，B树中所有节点的孩子个数的最大值称为B树的阶，通常用m表示。一颗m阶B树或为空树，或为满足如下特性的m叉树：
（1）树中每个节点至多有m棵子树，即至多含有m-1个关键字。
（2）若根节点不是终端结点，则至少有两棵子树。
（3）除根节点外的所有非叶节点至少有⌈m/2⌉棵子树，即至少含有⌈m/2⌉-1个关键字。（⌈⌉表示向上取整，例如⌈1.001⌉ = 2）
（4）所有的叶结点都出现在同一层次上，并且不带信息，即指向叶子结点的指针为空。
（5）关键字的值：子树0<关键字1<子树1<关键字2<子树2<...(以此类推，类比二叉查找树 左<中<右)
很多人看到这些定义非常懵逼，包括我刚开始看见这么多定义的第一反应是，为什么这样定义，为什么要限制子树的个数和关键字的个数呢？这些特性呢，实际上是B树为了保证查找的效率而采取的一种策略。
二叉查找树相信大家都比较好理解，当我们在二叉查找树中查找某一个数时，我们首先会和当前节点比较，如果该数比当前节点小，则去它的左子树中继续去找，如果比当前节点大，则去它的右子树中去找，直到找到或者查找失败，查找失败所在的叶子节点就是这个数所在的被该二叉查找树的节点所划分出来的范围。
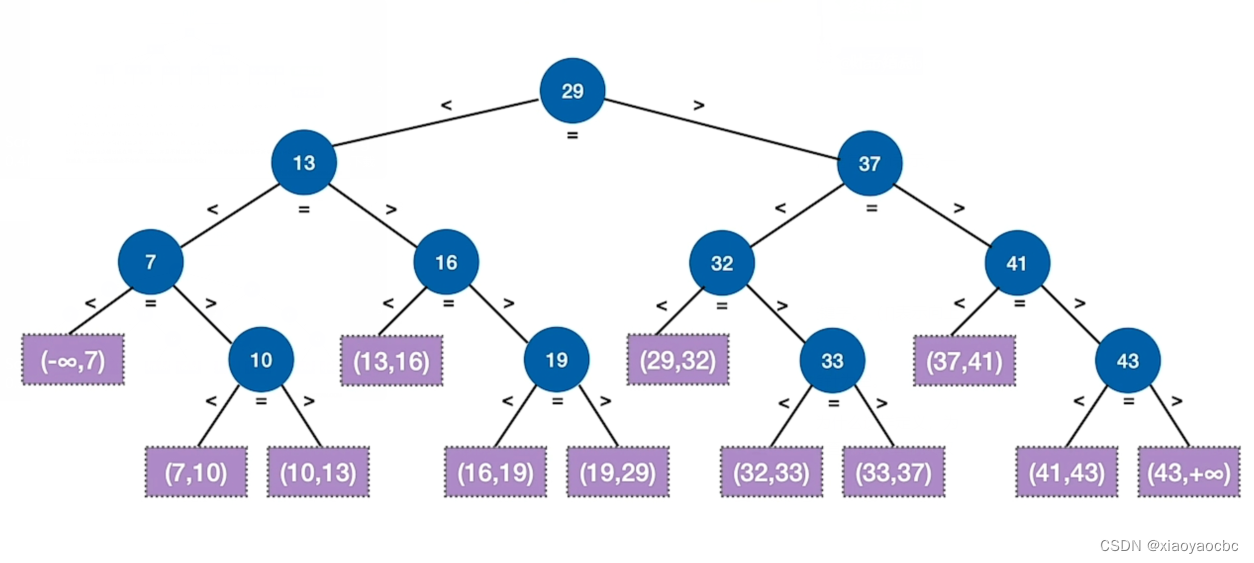
比如说我找20，最后会指向19这个节点的右子树，这个右子树所代表的范围就是(19,29)。
举个例子来说，数据库大家肯定都不陌生，比如现在有一张表，其中有100万条记录，现在要查找查找其中的某条数据，如何快速地从100万条记录中找到需要的那条记录呢？大家的第一反应肯定是二叉查找树，下面先谈谈为什么二叉树不行。
如果使用二叉查找树，那么这个二叉查找树的高度为
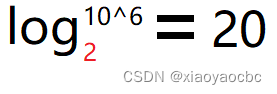
也就是说，要找到我们需要的那条数据，最差的情况下可能要进行20次比较，并且在数据库中，我们的数据量可能更加庞大，并且一般来说，表的索引本身也很大，不可能全部存储在内存中，一般要存储在磁盘上，用的时候再读入到内存，比较一次大小，这时候就产生了一次IO操作，这个IO操作的耗时比比较两个数的大小的耗时要多得多。比如常见的7200RPM的硬盘，摇臂转一圈需要60/7200≈8.33ms,换句话说，让磁盘完整的旋转一圈找到所需要的数据需要8.33ms,这比内存常见的100ns慢100000倍左右，这还不包括移动摇臂的时间。所以在这里制约查找速度的不是比较次数，而是IO操作的次数，而我们可以认为IO操作的次数就大约等于树的高度。而二叉树对于我们来说实在是太“瘦”太“高”了，因此在数据库和文件系统中我们不采取二叉树。
为了提高效率，我们就要让这棵树的高度尽可能的小，在高度公式中，有两种方式可以让值减小，一种是让真数小，一种是让底数大，而在实际应用中，真数表示的是数据的数量，是我们无法控制的，所以我们只能选择让底数变大，而这个底数就是这颗树的“叉”，二叉树的底数就是二，五叉树的底数就是五。
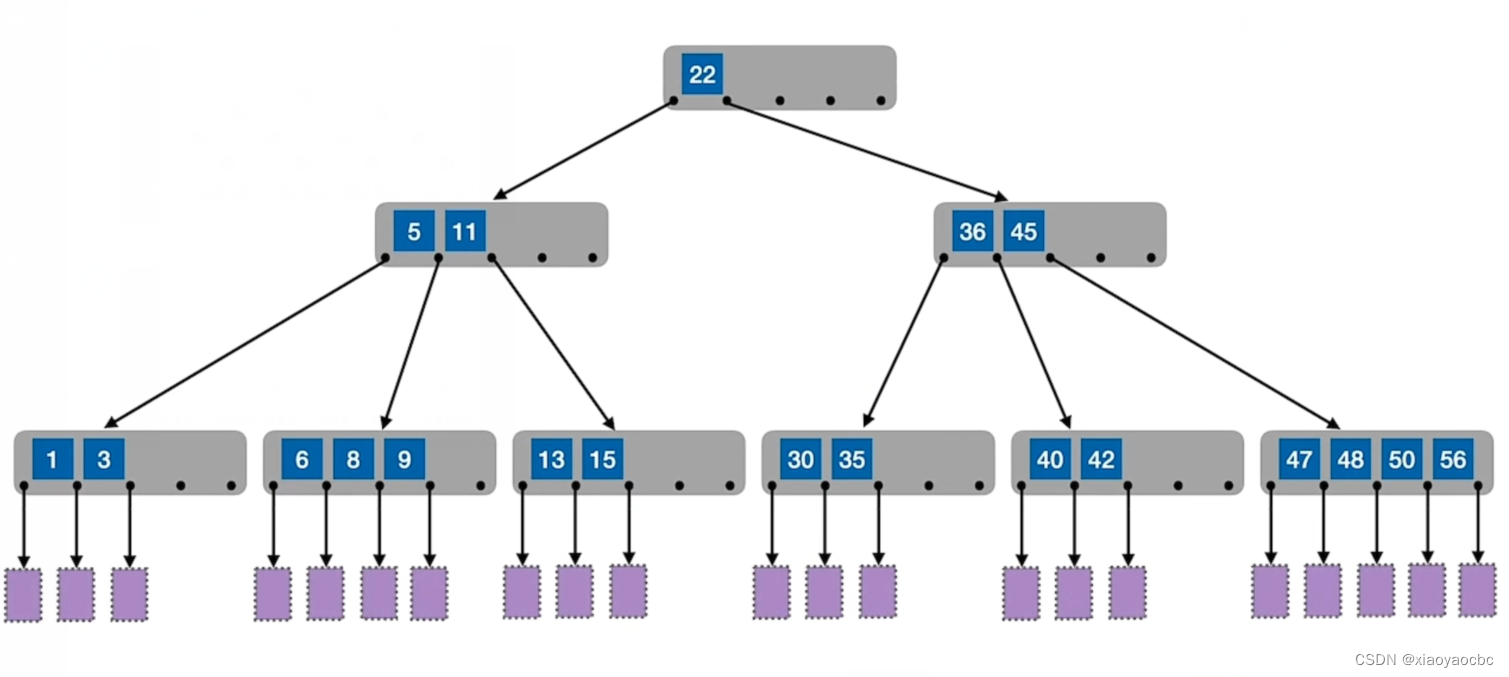
如图，这是一个五叉查找树，它和二叉查找树的规律是一样的，只不过二叉查找树的每个节点的关键字都只有一个，而这个五叉查找树的每个节点关键字最多有四个 ，为什么是四个呢？通俗的解释就是因为五叉查找树的每个节点最多有五个孩子节点，也就是说最多可以被划分为五个范围，由小学学习的植树问题可以知道，划分为五个范围需要四个关键字，所以关键字的个数最大值为x-1，x就是x叉树的x，也就是x阶b树的x。而我们又知道，若每个节点内关键字太少，导致树变高，那么我们查找效率就变低了，所以b树采取的策略就是：m阶b数，或者说m叉查找树中，任何节点至少有⌈m/2⌉个分叉，即至少含有⌈m/2⌉-1个关键字。也就是我们定义中的第三点。当然，我们要将根节点除外，因为当这棵树刚输入数据时，比如只有一个数据时，根节点只有两个分叉，是不符合定义的。
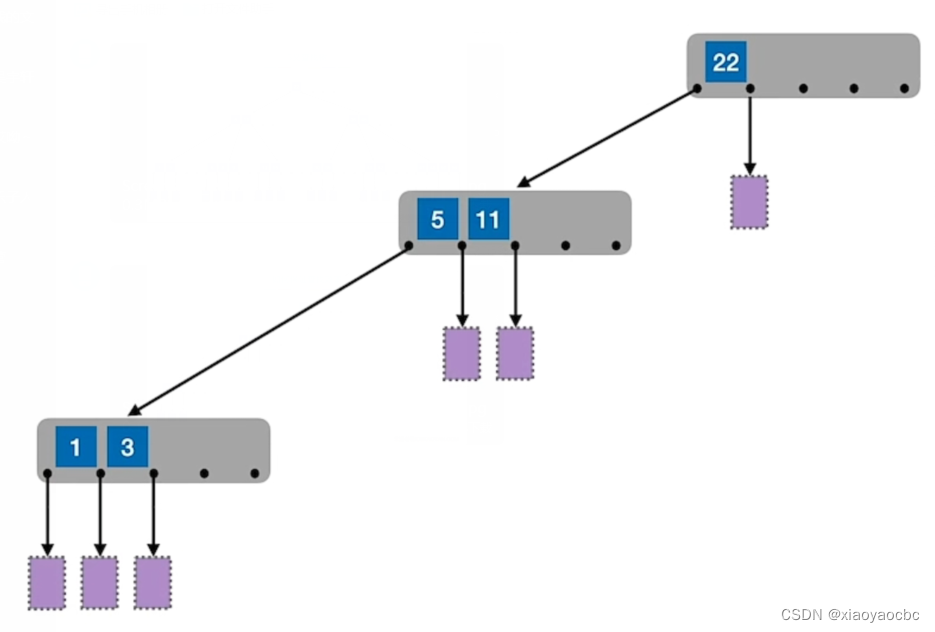
另外，如果说我们的五叉查找树如上图所示，它是符合我们上一条定义的，但是它的高度计算不符合我们刚开始的公式了，所以我们要求我们的b树应该是一个平衡的x叉树，它采取的策略是：m叉查找树中，规定对于任何一个节点，起所有子树的高度都要相同，也是我们定义的第四点。
2.B树的存储结构
#define m 3 // B树的阶，此设为3
typedef int KeyType;typedef struct BTNode {int keynum; // 结点中关键字个数，即结点的大小struct BTNode* parent; // 指向双亲结点KeyType key[m + 1]; // 关键字向量，key[0]未使用struct BTNode* ptr[m + 1]; // 子树指针向量
} BTNode, *BTree; // B树结点和B树的类型3.B树的查找操作
B-树的具体查找步骤如下（假设查找的关键字为key）：
1.先让key与根结点中的关键字比较，如果key等于key[i]（key[]为结点内的关键字数组），则查找成功。
2.若key
4.若key[i]
typedef struct
{BTree pt; // 指向找到的结点int i; // 1..m，在结点中的关键字序号int tag; // 1:查找成功，0:查找失败
} Result;void SearchBTree(BTree t, KeyType key, Result& r)
{int i = 0;int found = 0;BTree p = t; // 一开始指向根结点，之后指向待查结点BTree q = NULL; // 指向待查结点的双亲while (p != NULL && found == 0) {i = Search(p, key);if (i <= p->keynum && p->key[i] == key) {found = 1;}else {q = p;p = p->ptr[i - 1]; // 指针下移}}if (1 == found) { // 查找成功，返回key的位置p和ir.pt = p;r.i = i;r.tag = 1;}else { // 查找失败，返回key的插入位置q和ir.pt = q;r.i = i;r.tag = 0;}
}int Search(BTree p, KeyType key)
{int i = 1;while (i <= p->keynum && key > p->key[i]) {i++;}return i;
}4.B树的插入操作
与二叉排序树一样，B-树的创建过程也是将关键字逐个插入到树中的过程。
B树的插入首先要查找关键字ķ的插入位置。若该关键字存在于B树中，则不用插入直接返回，否则查找操作必定失败于某个最底层的非终端结点上，也就是要插入的位置。插入分两种情况讨论。
1.插入关键字后该结点的关键字数小于等于m-1，插入操作结束。
2.插入关键字后该结点的关键字数等于m，则应该进行分裂操作，分裂操作如下：
1.生成一个新结点，从中间位置把结点（不包括中间位置的关键字）分为两部分。
2.前半部分留在旧结点中，后半部分复制到新结点中。
3.中间位置的关键字连同新结点的存储位置插入到父结点中，如果插入后父结点的关键字个数也超过了m-1，则继续分裂。
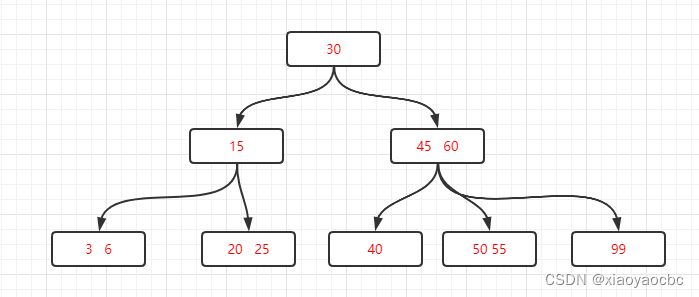
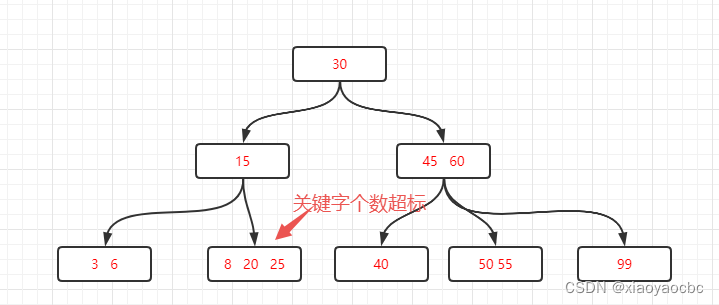
比如在上图三阶B树中插入18，查找发现关键字位置在 20 25节点，插入后关键字变为8 20 25，有三个，而三阶B树的每个节点最多有3-1=2个关键字，所以应该调整结构进行分裂操作。
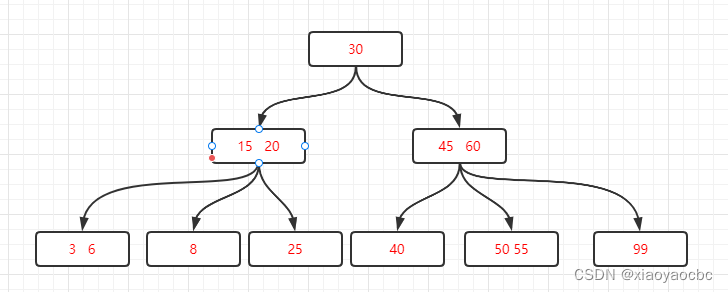
从中间节点，即第 ⌈3/2⌉ = 2个节点分开，左边8，中间20，右边25，前半部分留在旧结点中，后半部分复制到新结点中，中间位置的关键字连同新结点的存储位置插入到父结点中。结果变成下图的B树。
5.B树的删除操作
对于B-树关键字的删除，需要找到待删除的关键字，在结点中删除关键字的过程也有可能破坏B-树的特性，如旧关键字的删除可能使得结点中关键字的个数少于规定个数，这样就需要从兄弟结点借关键字或者合并。
情况一：删除后关键字数量不小于⌈m/2⌉，则直接删除即可。
情况二：关键字个数等于⌈m/2⌉-1，而且该结点相邻的右兄弟（或左兄弟）结点中的关键字数目大于⌈m/2⌉-1。比如删除上图中的40关键字。删除后这个结点的关键字数量为0，我们需要把右兄弟结点中的最小关键字50上移，替换关键字45，关键字45则放进40所在的结点中。
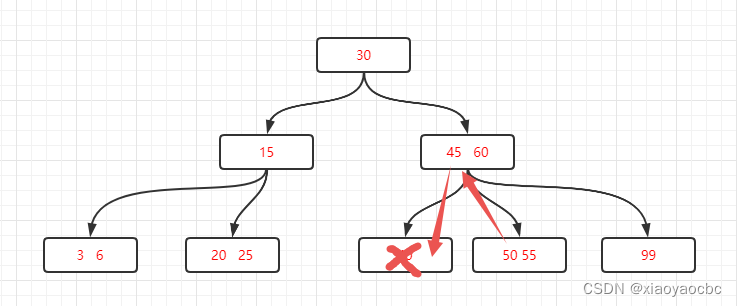
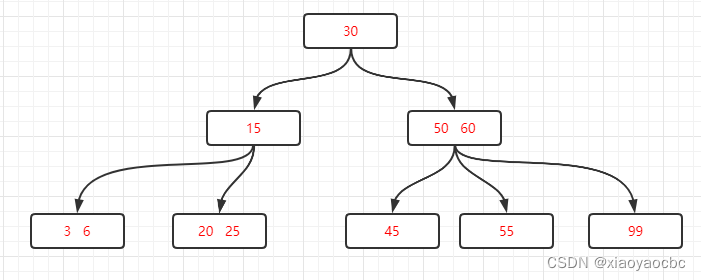
第三种：关键字个数Ñ等于⌈m/2⌉-1，而且被删除关键字所在结点和其相邻的兄弟结点中的关键字数目均等于[M / 2] -1。也就是说无法从兄弟节点借了，那么这个结点就不存在了，兄弟结点就需要合并父亲结点。比如说在上图的基础上继续删除45关键字。
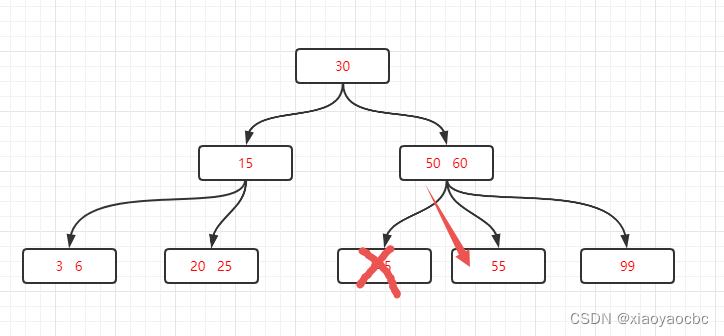
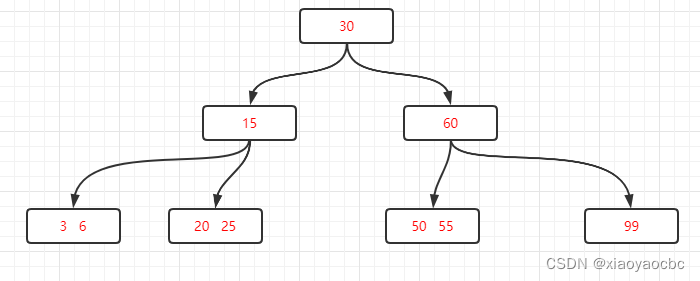
二、B+树
1.B+树的定义
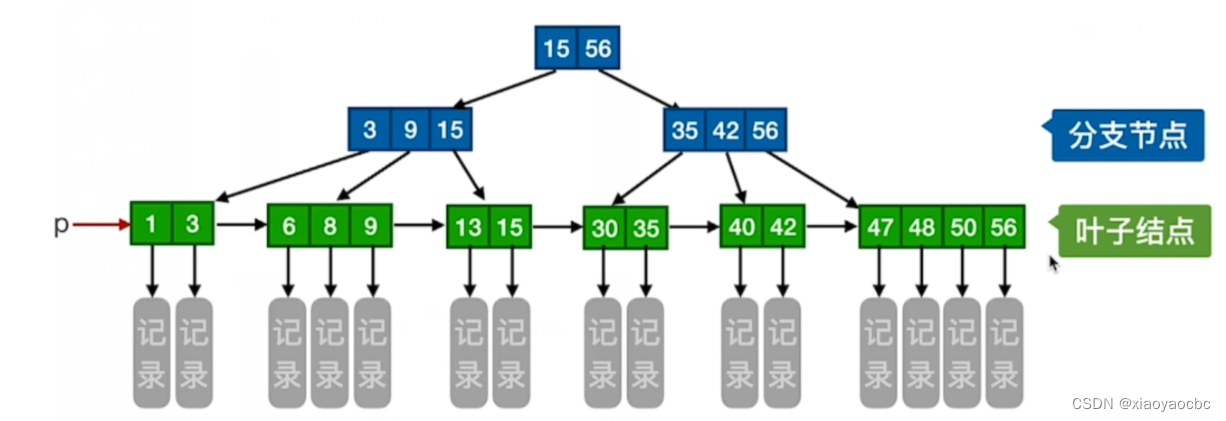如上图，这是一棵4阶B+树，一棵m阶的B+树需满足下列条件：
（1）每个分支结点最多有m棵子树（孩子结点）。
（2）非叶根节点至少有两棵子树，其他每个分支结点至少有⌈m/2⌉棵子树。
（3）结点的子树个数与关键字个数相等。
（4）所有叶结点包含全部关键字及指向响应记录的指针，叶结点中将关键字按大小顺序排列，并且相邻叶节点按大小顺序相互链接起来。（支持顺序查找）
（5）所有分支结点中仅包含它的各个子结点中关键字的最大值及指向其子节点的指针。
2.为什么要有B+树
要说明这个问题，首先要从B树的好处和不足出发。
B树好处：
B树的每一个结点都包含key(索引值) 和 value(对应数据)，因此方位离根结点近的元素会更快速。（相对于B+树）
B树的不足：
B树在提高了IO性能的同时并没有解决元素遍历的我效率低下的问题，不利于范围查找(区间查找)，如果要找 0~100的索引值，那么B树需要多次从根结点开始逐个查找。正是为了解决这个问题，B+树应用而生。B+树由于叶子结点都有链表，且链表是以从小到大的顺序排好序的，因此可以直接通过遍历链表实现范围查找。B+树只需要去遍历叶子节点就可以实现整棵树的遍历。而且在数据库中基于范围的查询是非常频繁的，而B树不支持这样的操作或者说效率太低。B+树支持range-query(区间查询)非常方便，而B树不支持。
同时，在B+树中，非叶结点不含有该关键字对应记录的存储地址，可以使一个磁盘块可以包含更多个关键字，使B+树的阶更大，树高更矮，读磁盘次数更少，查找更快。因此B+ 树通常用于数据库和操作系统的文件系统中。
NTFS, ReiserFS, NSS, XFS, JFS, ReFS 和BFS等文件系统都在使用B+树作为元数据索引。B+树的特点是能够保持数据稳定有序，其插入与修改拥有较稳定的对数时间复杂度。B+树元素自底向上插入。
本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！