【牛客】阶乘（唯一分解定理+二分）：

【题目传送门】 here~

题目描述

给定一个正整数 p 求一个最小的正整数 n，使得 n! 是 p 的倍数

输入描述:

第一行输入一个正整数T表示测试数据组数接下来T行，每行一个正整数p

输出描述:

输出T行，对于每组测试数据输出满足条件的最小的n

示例1

输入

4
1
2
4
8

输出

1
2
4
4

备注：

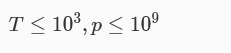
首先这一题涉及到了唯一分解定理,
那么什么是唯一分解定理呢，在我们分析思路之前，来让我们看一下百度百科的解释 ~

任何一个大于1的自然数 N,如果N不为质数，那么N可以唯一分解成有限个质数的乘积N=P₁ ^a1 * P₂^a2 * P₃^a3 … P_n^an，这里P₁23…n均为质数，其中指数ai是正整数。这样的分解称为 N 的标准分解式。最早证明是由欧几里得给出的。
解释的很清楚，下面来给出个例子：
48 --> 6 * 8 --> 2 * 3 * 4 * 2 --> 2 * 3 * 2 * 2 * 2 --> 2⁴ * 3¹;

分析思路：

• 了解完唯一分解定理之后，我们可以知道要满足N！是P的倍数的话，可以先对N!和P都使用唯一分解定理，需要使N!分解出来每个质数的指数都大于等于 P分解出来的每个质数的指数；（不太好描述，看例子比较好理解）
  这里举个例子来帮助了解一下：假设我们的p=48,利用唯一分解定理得到p=2⁴ * 3¹（注意这里2的指数和3的指数）;要使N！是p的倍数，则 N!使用唯一分解定理后的得到的式子必须满足N!= 2^a * 3^b * c; 若满足条件则必须使 a>=4 && b>=1 && c>=1;

• 我们明确了要查找的N！要满足的条件之后，我们可以看到这一题的数据范围非常大达到1e9，这个时候我们就要考虑利用二分来查找，取l=1，r=1e9;如果mid符合条件那么我们就舍弃左边部分，因为是阶乘，如果mid不符合条件，那么1-mid也都是不符合，因此舍弃左边部分，然后一直维护ans的值即可。

AC代码：

#include
using namespace std;
const int maxn=1e6+100;
int prime[maxn],num[maxn];
//prime:质因子 num：质因子出现次数
int k,t,p;//质因子的个数；
bool check(int x)//检查这个数满不满足条件 
{for(int i=1;i<=k;i++){int primernum=0,n=x;//primernum是判断的这个数，有几个prime[i]这个质因子数while(n){primernum+=n/prime[i];n/=prime[i];}if(primernum<num[i])return false;//保证N!(即primernum)分解出来每个质数的指数都大于等于 P分解出来的每个质数的指数;}return true;
}
void solve()
{k=0; //这里利用唯一分解定理的思想 for(int i=2;i*i<=p;i++)// 求出p的所有质因子 {if(p%i==0){prime[++k]=i; //prime数组表示P的所有质因子 while(p%i==0){num[k]++;//num数组就是每个质因数的指数 p/=i;}}}if(p>1) prime[++k]=p,num[k]++;//最后一个质因子 int l=1,r=1e9,mid,ans;while(l<=r) {mid=(l+r)/2;if(check(mid)){r=mid-1;ans=mid;}else l=mid+1;}memset(prime,0,sizeof prime);//多实例测试，所以要清空两个数组； memset(num,0,sizeof num);cout<<ans<<endl; 
}
int main()
{cin>>t;while(t--){cin>>p;solve();}return 0;
}

第四道~~
还没写完，不小心发出来了，下午接着写。QAQ
（已完善 ~~

Thank you for watching ！

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！