我的《电路》学习

1-3 基本电路物理量：电流、电压、电功率和能量

1、电流定义：

        顾名思义：电流指的是电荷的移动

        学术定义：单位时间内流过的电荷量

           其中q是电荷量，t是时间，i是电流

        电流的通用的定义是

2、电压定义

        顾名思义：电压指的是电荷的压力

        学术定义：单位点电荷从一点移动到另外一点所做的功

        其中u是电压，W是功，q是电荷量

        电流的通用的定义是

3、功率定义

        功率的定义：单位时间内做的功

        功率的通用定义是

        

        能量：

1-4 电流和电压的参考方向

1、规定正电荷的运动方向为电流的实际方向

电流实际方向很难判断，对于一个元件，要指定电流参考方向：任意假定一个正电荷运动的方向为电流的参考方向。

电流的参考方向与实际方向的关系

如果电流是实际方向与参考方向相同，则i>0，如果电流的实际方向与参考方向相反，则i<0

指定参考方向后，根据电流的正负就可以判断电流的实际方向。

规定参考方向以后，才能写出电流的函数式。i(t)=50cos(wt)

2、电流参考方向的两种表示

1、用箭头表示：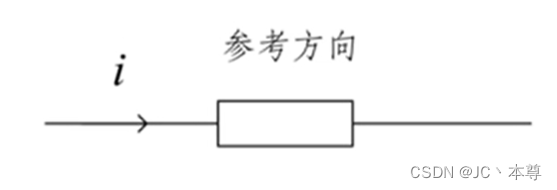

 2、用双下标表示，表示电流的参考方向是由A到B

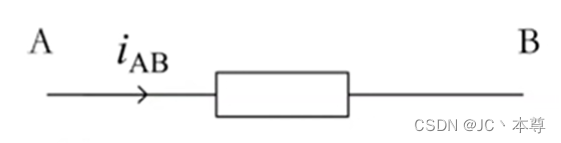
 3、电压的参考方向

规定电压的实际方向从高电位指向低电位亦即电位降低的方向

在复杂电路或电压随时间变化时，两点间电压的实际方向难以判断

需要指定电压的参考方向或参考极性

正极性（+）表示高电位        负极性（-）表示低电位

正极指向负极的方向就是电压的参考方向

4、在指定电压的参考方向以后电压就是一个代数量

假定左端的电位比右端电位高，如果实际情况左端电位>右端电位，u>0

如果实际情况左端电位<右端电位，u<0

5、电压参考方向的三种表示方式

1、用箭头表示：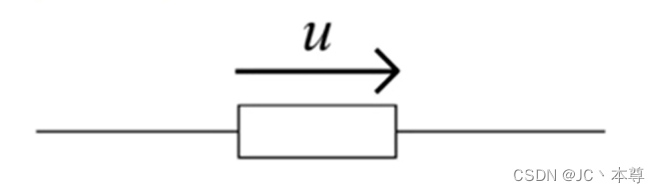

 2、用正、负极性表示：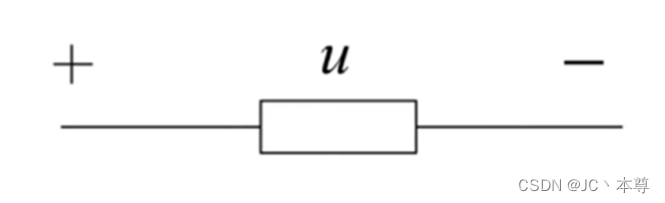

 3、用双下标表示：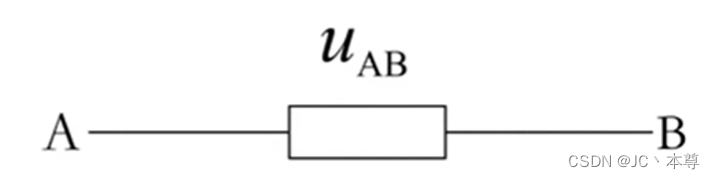

6、关联参考方向

元件或支路的u，i采用相同的参考方向称为关联参考方向。反之，称为非关联参考方向

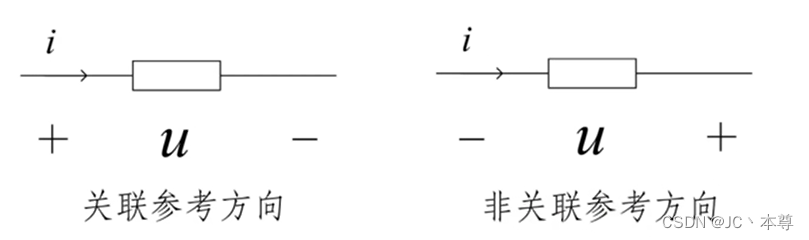
特别注意：

1、分析电路前必须指定电压和电流的参考方向。

2、参考方向一经指定，必须在图中相应位置标注（包括方向和符号)。

3、参考方向不同时，其表达式相差一个负号，但电压、电流的实际方向不变

7、电功率与电流电压参考方向的关系

p与u和i的方向密切相关

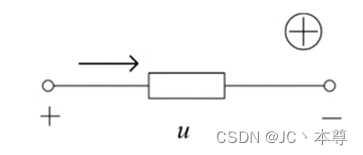
当正电荷从元件上电压的正极经元件运动到电压的负极时，与此电压相应的电场力要对电荷做功，这时元件吸收能量，此时电流的方向与电压相同。

反之，当正电荷从电压的负极运动到电压的正极时，电场力做负功，元件向外释放电能，此时电流的方向与电压相反。

元件中功率和能量分别是

       

在指定电压和电流的参考方向后，由于u、i都是代数量，

功率p和能量W都是代数量

随着电压电流参考方向的不同，功率表示的含义不同

1、电压和电流的参考方向为关联参考方向时

乘积“ui”表示元件吸收的功率

p>0        实际吸收功率

p<0        实际发出功率

2、电压和电流的参考方向为非关联参考方向时

乘积“ui”表示元件发出的功率

p>0        实际发出功率

p<0        实际吸收功率

对一完整的电路，发出的功率=吸收的功率

1-5 电路元件-电阻

电阻元件的元件特性——u与i的代数关系f(u,i)=0

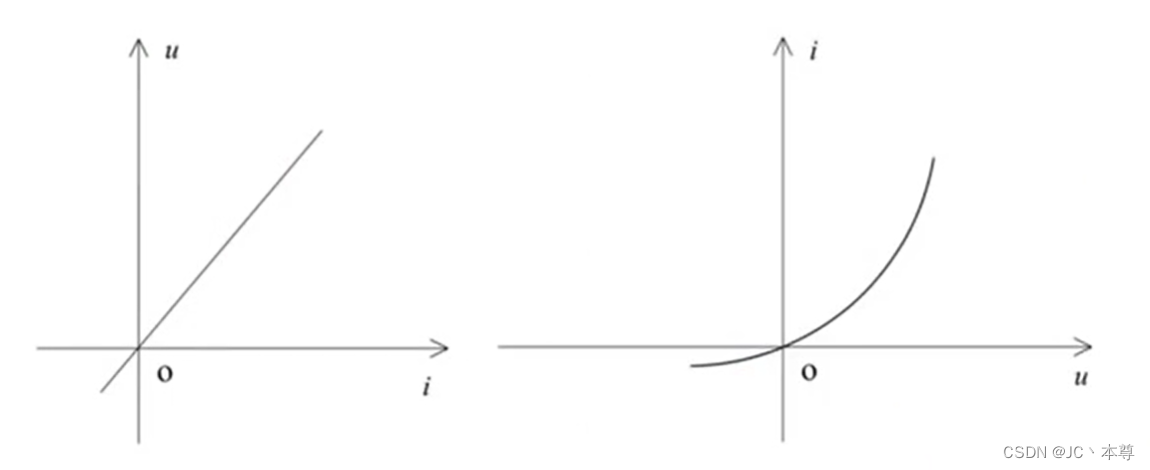
 1、线性电阻元件

在电压和电流取关联参考方向时，两端的电压和电流服从欧姆定律

R为电阻元件的参数，称为电阻，电阻的单位为Ω（欧姆，简称欧）。

线性电阻元件的图形符号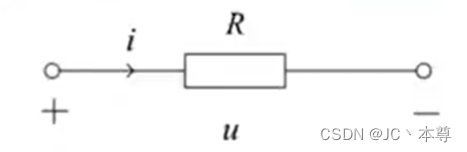

其中称为电阻元件的电导。单位是S（西门子，简称西）R和G都是电阻元件的参数。

如果电压、电流参考方向取非关联参考方向，则或

电阻元件的特性称为伏安特性，它是通过原点的一条直线。

欧姆定律

①只适用于线性电阻（R为常数）

②电压与电流参考方向非关联，欧姆定律表示为或

③线性电阻是无记忆、双向性的元件，公式和参考方向必须配套使用，有关电压电流的表达式都是在指定参考方向下给出的。

2、电阻元件的功率和能量

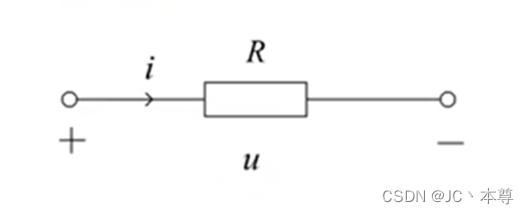
 当u和i取关联参考方向时，电阻元件吸收的功率为，表明电阻元件在如何时刻总是吸收功率。线性电阻元件是耗能元件，电阻元件从到时间内吸收的电能为

3、开路和短路

对于电路中的一对端子1-1'

端子1-1'之间断开时，相当于接的电阻，i=0，u≠0，称1-1'处于“开路”。

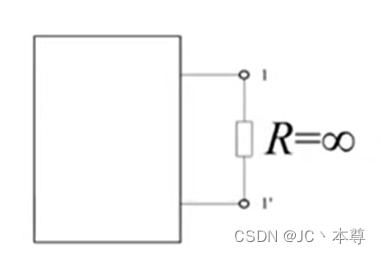
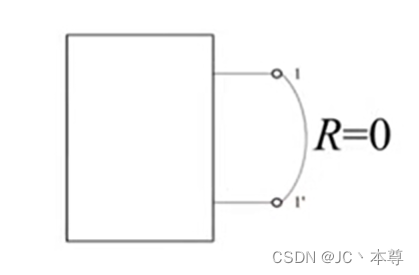
端子1-1'用理想导向（电阻为零）连接起来，相当于接有R=0的电阻

u=0，i≠0，称1-1'处被短路。

1-6 电压源和电流源

1、电压源

顾名思义：就是能够提供电压的电源，比如电池、手机电池、直流稳压电源、发电机（交流源）

电压源可以是直流源也可以是交流源还可以是其他形式，所以无法用电池符号简单的来代替

电压源的通用符号电压源的正负极代表的是参考电压的正负极，电压源的特点是电压由自身确定电流由外电路确定。

2、电流源

顾名思义：就是能够提供电流的电源，电流源的符号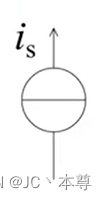电流源的箭头方向代表的是参考电流的方向，电流源的特点是电流由自身确定，电压由外电路确定。

1-7 受控电源（受控源）

定义：电压或电流受其他电压或电流控制的电源。通常所说的电压源和电流源称为独立电源，其电压或电流由自身产生，不受其他电压电流控制。

受控源分类：受控电压源和受控电流源

受控电压源的符号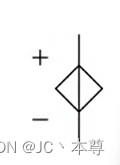：独立电压源的符号：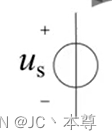

受控电流源的符号：独立电流源的符号：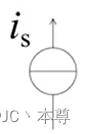

控制量有电压和电流两种情况，所以受控电源共有4种类型

受控源有四种类型：

电压控制电压源，其中k是没有单位的常数。

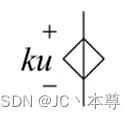
电流控制电压源，其中k是常数单位是Ω欧姆

电压控制电流源，其中k是常数单位是S西门子

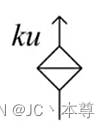
电流控制电流源，其中k是没有单位的常数

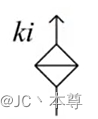
1-8 基尔霍夫电流定律（KCL）

1、基尔霍夫电流定律

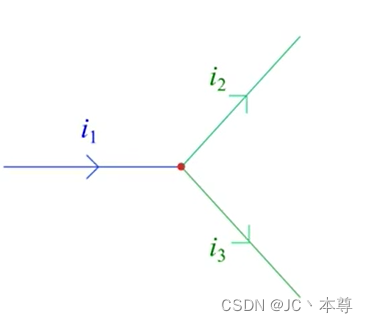
         即流入电流=流出电流，基尔霍夫电流定律，简称KCL

基尔霍夫电流定律的内容是电路中任一结点上所有电流的代数和为零，即，正和负取决于这个电流是流入还是流出

2、广义结点、KCL独立方程数

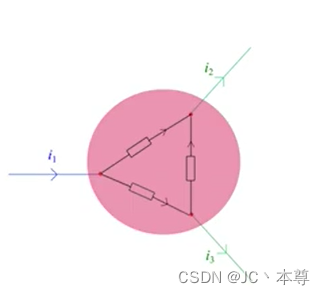
 任意封闭曲线（曲面）都可以视为广义结点

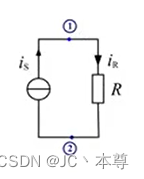以流入电流为正

结点1KCL方程：

结点2KCL方程：，两个结点的KCL方程只有一个KCL方程是独立的。

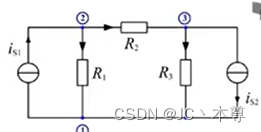
 结点1KCL方程：

结点2KCL方程：

结点3KCL方程：,三个结点KCL方程左端相加等于零，所以，由其中两个方程可以推出第三个方程，三个方程中只有两个是独立方程。

对于具有n个结点的电路，需要列些的独立KCL方程数为n-1

1-9 基尔霍夫电压定律

电场力做工与路径无关

基尔霍夫电压定律（KVL）：

形式1：在电路中，任一时刻，沿任一回路绕行，各支路的代数和等于零。

即，电场力做正功电场力做负功，降压取“+”，升压取“-”

形式2：升压=降压

                

                         

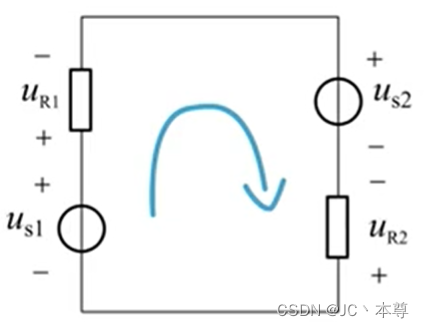
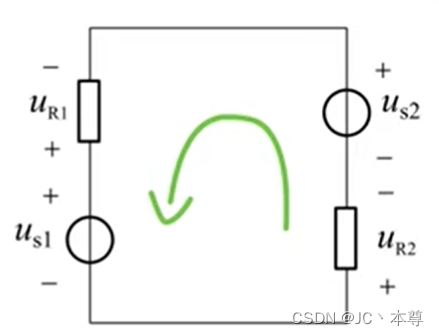
                                各支路电压的代数和为零。

        升压=降压          

列写KVL方程前需要事先指定各支路电压参考方向和回路方向，回路绕向会影响代数和中各支路电压项前面的正负号

2-1 电路的等效变换

1、等效变换

等效变换是将电路中某一部分进行变换，变换后该部分外部端口的电压电流值都保持不变或者说外部端口的电压电流关系都保持不变。

等效变换的特点：

（1）对外等效。原因是外部端口电压电流不变，在外电路看来一切保持原样

（2）对内不等效。原因是内部电路进行了变换。

2-2 电阻的串联和并联

n个电阻串联，可以等效为一个电阻

n个电阻并联，可等效为一个电阻，

2-3 电压源、电流源的串联和并联

1、电压源的串联和并联

一、理想电压源的串联和并联

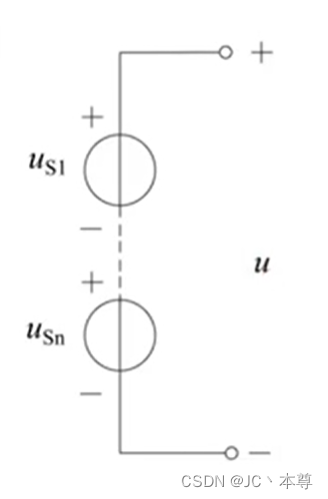
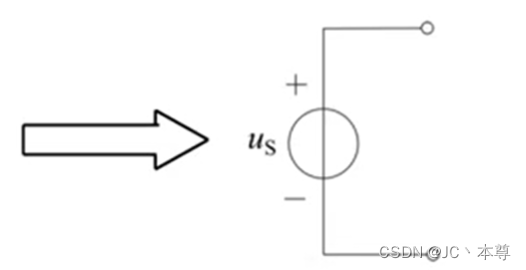
上图为多个电压源的串联，由KVL可知，

所以n个电压源的串联可以用一个等效电压源替代。

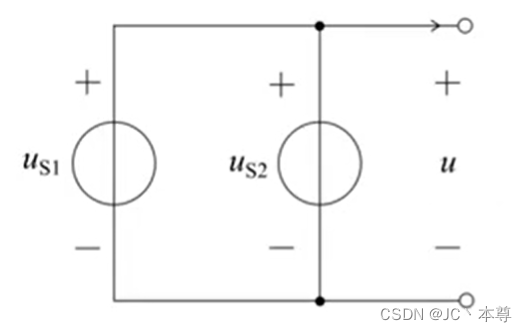
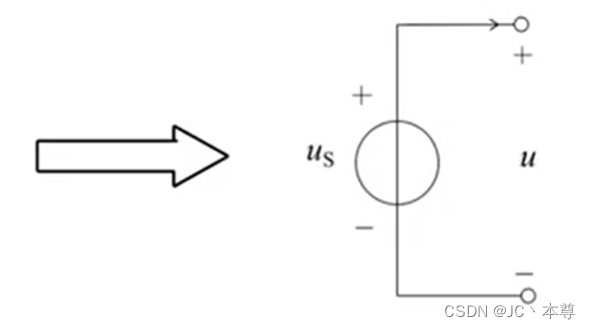
 上图为两个电压源的并联，根据KVL，，

注意只有相同的理想电压源才能并联。

二、电压源与支路的串、并联等效

 

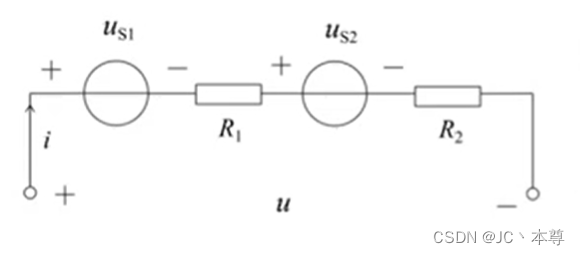
 根据KVL，

其中可以用来表示，可以用R来表示，因此这个电路可以用一个电压源与一个电阻的串联等效表示

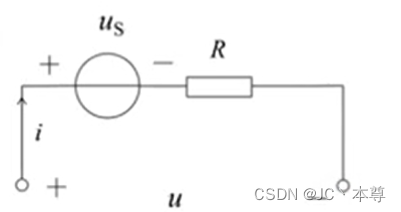
 图中，

2、电流源的串联和并联

一、理想电流源的串联和并联

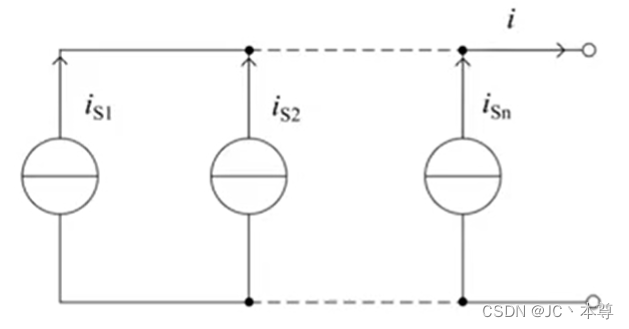
上图是n个电流源的并联，由KCL得，总电流

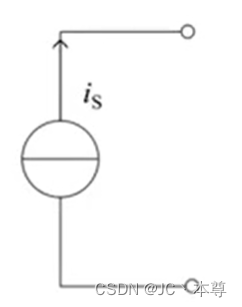
因此我们可以用一个电流源来等效如上图，

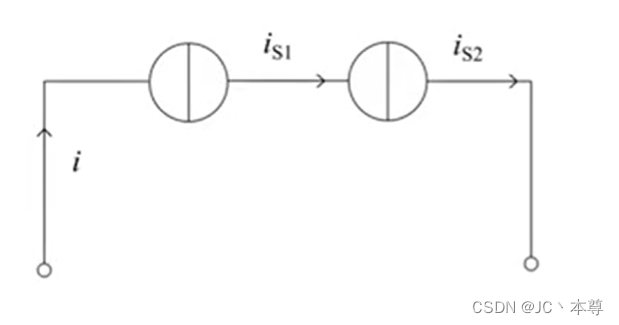
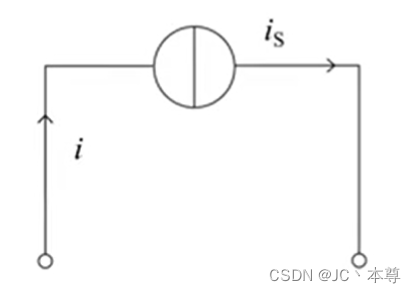
等效电流源，

二、电流源与支路的串、并联等效

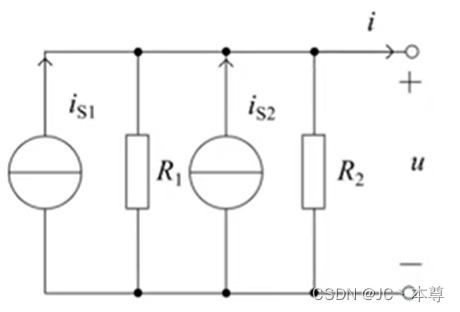
根据KCL，

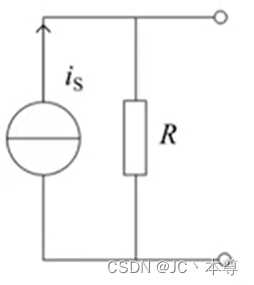图中，        

2-4 实际电源的两种模型及其等效变换

实际电压源：理想电压源和电阻（内阻）串联，这个电阻通常非常小

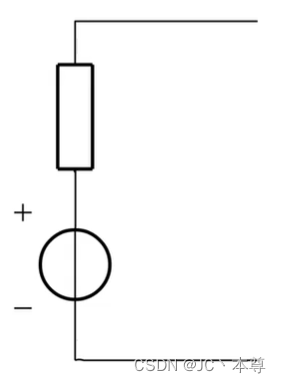
实际电流源：理想电流源和电阻（内阻）并联，这个电阻通常非常大

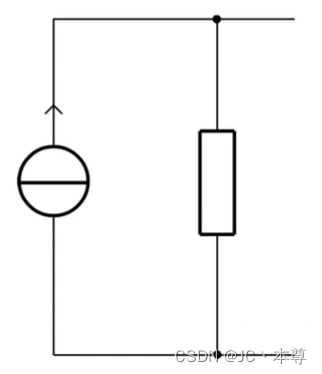
这两种模型可以进行相互的等效变换 

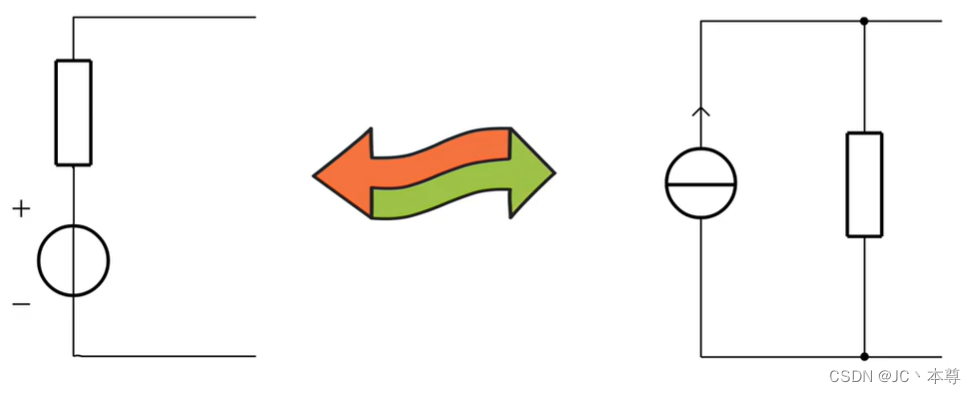
对于实际电压源的模型

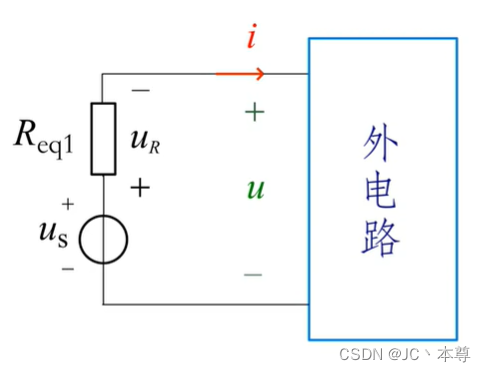
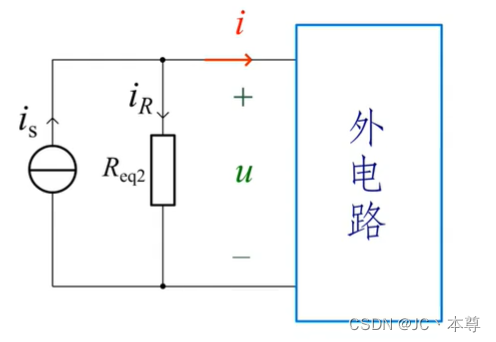
要保证是等效变换，那么

3-1 回路电流法

一、与回路电流法和结点电压法相关的概念

支路：每一个二端元件称为一条支路，多个二端元件串联可以视为一条支路。

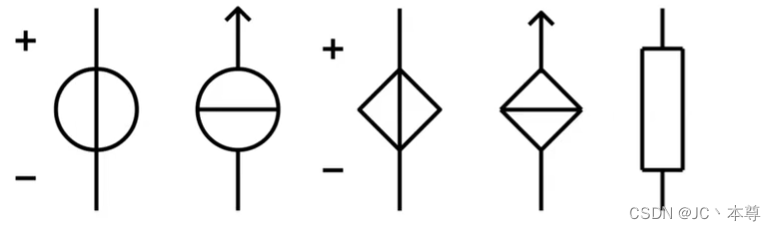
结点：支路与支路的连接点称为结点

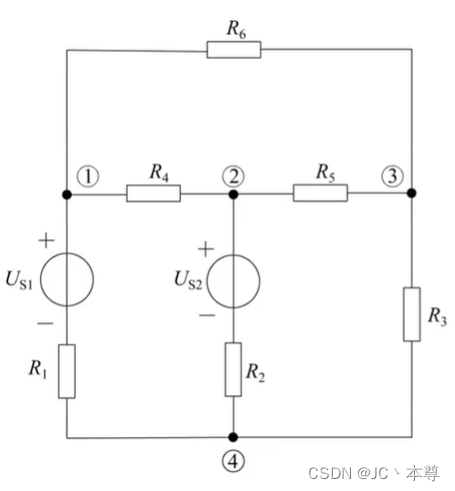
 图中①②③④都是结点

多个等电位的结点可视为一个结点。

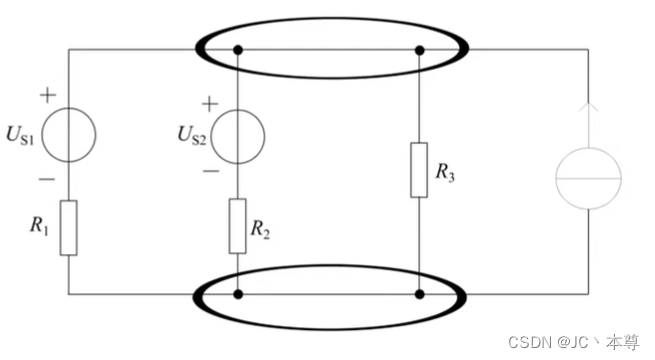
图中上下两个黑圈内的结点都可分别视为一个结点

路径：从一个结点到另一个结点所经过的支路的集合。

回路：从起点出发，终点又回到起点，所形成的闭合路径称为回路。要求中间经过的结点只能经过一次。

网孔：能令回路中不另外含有支路的回路称为网孔。网孔数量等于KVL独立方程数，所以，判断KVL独立方程数的简单方法是数网孔的数量。

二、回路电流法由来

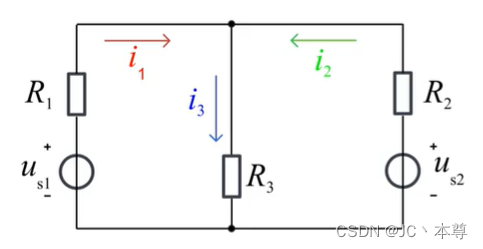
 如图可以写出

1个KCL方程：，

2个KVL方程：

                       

为了减少方程数，将拆分成和如图

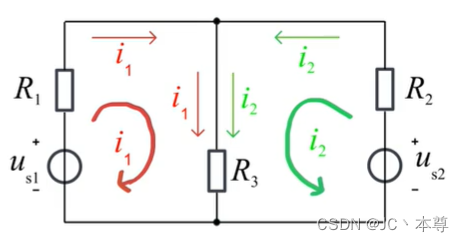
左边的同名电流可以形成一个回路电流，右边的同名电流也可以形成一个回路电流

所以在列写回路电流方程的时候就不用列写KCL方程，只需要列写KVL方程

2个KVL方程：

                       

三、回路电流方程列写

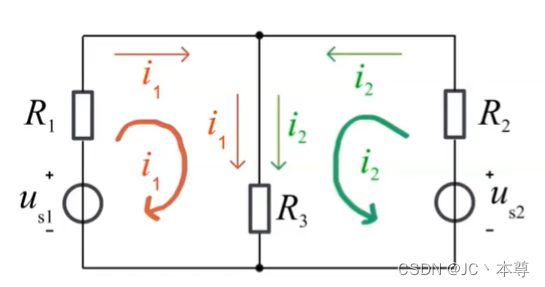
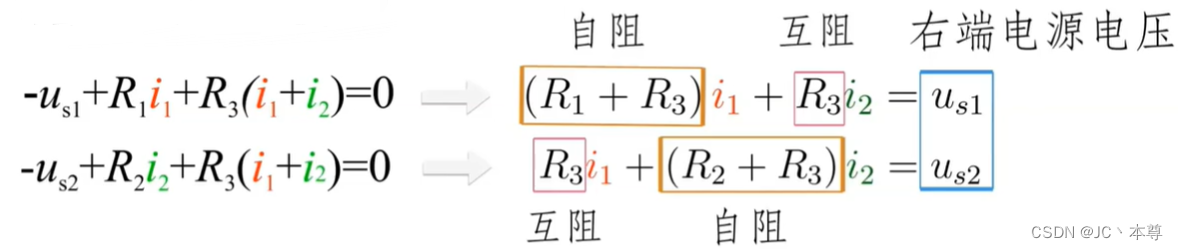
 自阻项前永远取正，互阻有正有负，互阻上回路电流同方向取正，相反取负。右端电源电压项有正有负，非关联取正，关联取负。

3-2 结点电压法

一、参考结点和独立结点

1、结点电压法

        以结点为独立变量列写电路方程的分析方法。

结点电压：在电路中任意选择一个结点为参考结点，其他结点为独立结点，结点电压就是独立结点与参考结点之间的电压。

参考极性：以独立结点为正，以参考结点为负。

由KVL可知，支路电压就是两个结点电压之差，所有支路电压都可以用结点电压表示。用结点电压作为独立变量，KVL自动满足。

结点电压法：以结点电压为独立变量，列写独立结点的KCL方程，共有（n-1）个独立方程，称为结点电压方程。

2、结点电压方程的列写

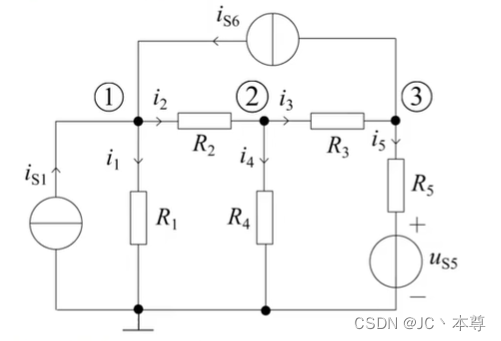
①选定参考结点，标明（n-1）个独立结点编号。

②列KCL方程，

结点1的方程：

结点2的方程：

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！