暑假刷题Day2--Codeforces Round 880 (Div. 2)

文章目录

目录

文章目录

前言

A. Destroyer

B. Astrophysicists

C. k-th equality

D. Lottery（补题）

前言

        这场的题目是真的难读

A. Destroyer

        链接：https://codeforces.com/contest/1836/problem/A

        题意：给定n个数，要求能组合成若干个 [0,1,2,3,....,x]的等差数列.

        思路：记录每个数字的个数 , 对于任意x ，满足即可

        代码：

#include 
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second 
const LL maxn = 4e05+7;
const LL N=1e05+10;
const LL mod=1e09+7;
typedef pairpl;
priority_queue, greater >t;
priority_queue q;
int cmp(int a,int b)
{return a>=1;}return sum;
}
void solve() 
{int n;cin>>n;int a[110];memset(a,0,sizeof a);for(int i = 0 ; i >num;a[num]++;}int f = 1;for(int  i = 1 ; i < 110 ;  i++){if(a[i] > a[i-1])f = 0;}if(f)cout<<"YES\n";elsecout<<"NO\n";
}            
int main() 
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);int t=1;cin>>t;while(t--){solve();}return 0;
}

B. Astrophysicists

        链接:https://codeforces.com/contest/1836/problem/B

        题意：（这题读题读了十几分钟orz）某公司准备发放k个价值为g的金币给n个科学家，当然，他们不打算以金币形式来发放，而是转换成了k*g个银币来发放。发放规则如下:假设准备为科学家发放x个银币，那么实际所发放的取决于数字， 如果 则需要额外发放(g-r)个银币，即总共发了 x + （g - r） 个银币 ，否则不需要发这r个银币了，那么公司就可以省下这笔钱。让你求出公司能够省的钱的最大值。

        思路：对于每一个人而言，能够省下的钱是有限的，若g为偶数则最多能够省下个银币，如果g为奇数则最多能够省下个银币。我们利用贪心思想，将前面n-1个人的钱全部省下来，然后再将剩下的（如果有的话）银币全部发放给最后一个人，最终算出能够省出的银币

        代码:

#include 
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second 
const LL maxn = 4e05+7;
const LL N=1e05+10;
const LL mod=1e09+7;
typedef pairpl;
priority_queue, greater >t;
priority_queue q;
int cmp(int a,int b)
{return a>=1;}return sum;
}
void solve() 
{LL n , k , g;cin>>n>>k>>g;LL sum = k * g;LL ans = 0;LL cost = 0;if(g % 2){cost = g/2;}else{cost = g/2 - 1;}if(cost * (n-1) <= sum){sum -= cost * (n - 1);ans += cost * (n - 1);}else{int k = sum / cost;sum -= cost * k;ans += cost * k;}if((sum % g) * 2 >= g){ans -= g - (sum % g);}elseans += sum % g;cout<>t;while(t--){solve();}return 0;
}

C. k-th equality

        链接:https://codeforces.com/contest/1836/problem/C

        题意:给你三个数a，b，c以及k，让你按照字典序求出第k个a位数+b位数=c位数的式子

        例如a = 1 ，b = 1 , c = 1 , k = 9， 那么前九个式子为:        因此需要输出2+1=3

        思路：暴力求解，观察到a，b的最大值为6，所以对a进行遍历能够在1e07个操作内完成，不会超时，在过程中注意下b的取值范围即可

        代码:

#include 
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second 
const LL maxn = 4e05+7;
const LL N=1e05+10;
const LL mod=1e09+7;
typedef pairpl;
priority_queue, greater >t;
priority_queue q;
int cmp(int a,int b)
{return a>=1;}return sum;
}
void solve() 
{int a , b , c;cin>>a>>b>>c;LL k;cin>>k;int a_min = pow(10,a - 1);int a_max = pow(10,a) - 1;int b_min = pow(10,b - 1);int b_max = pow(10,b) - 1;int c_min = pow(10,c - 1);int c_max = pow(10,c) - 1;for(int i = a_min ; i <= a_max ; i++){LL r = min(b_max , c_max - i);//b取值的右边界LL l = max(b_min , c_min - i);//b取值的左边界
//		cout< r)continue;if(r - l + 1 >= k){cout<D. Lottery（补题） 
        链接:https://codeforces.com/contest/1836/problem/D
 
        题意：有n个人分别拿了一张[0,m]区间内的彩票，假如中奖数字为x，那么这n个数当中最接近的k个数将成功中奖，如果距离一样，则小的那个数中奖。而你是第n+1个人，你知道这n个人的彩票数字，你可以任意选择你的彩票数字。求出最有可能让你中奖的那个彩票数字，同时给出在这种情况下有多少种可能。
 
        样例1：
 
Input
 
3 6 2
1 4 5
 
Output
 
4 2
 
在此情况之下，n=3，m=6，k=2，有两张彩票能够中奖，那么如果你选择2为你自己的数字，那多最多中奖数字可以为[0,1,2,3]，而3也是同样的，因为2小于3最终输入4  2
 
思路：
 
 
 
 
 
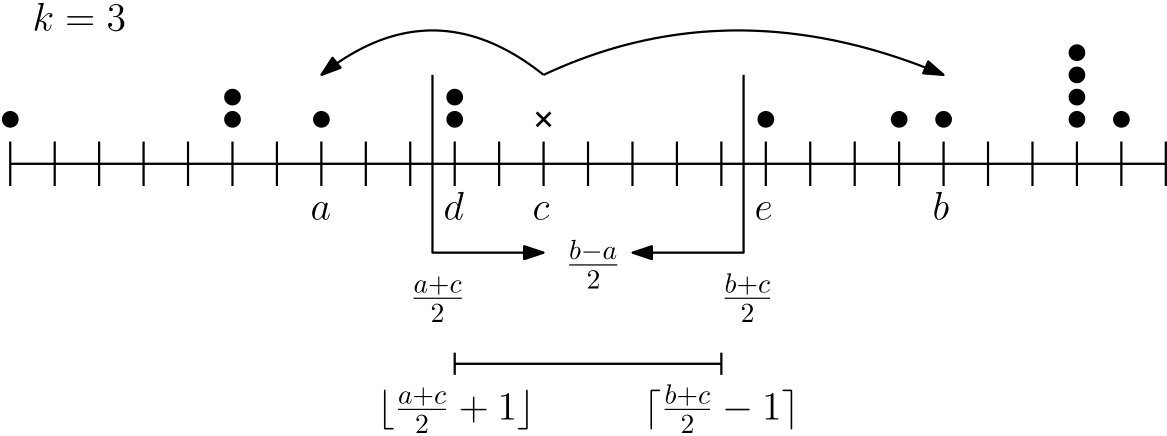
 当k=3时，假设你的彩票位于c的位置，如果只看c之前的位置，你需要和c之前的第k个人竞争这最后一个中奖名额（在这之间的是否中奖对你没有任何影响），因此你所能中奖的范围是,考虑c右边的情况也是如此，右边的k-1个人对于你是否中奖无关，只需要考虑第k个人的情况即可，因此中奖范围是。同时需要考虑特殊情况，如果前面没有k个人那么从均可满足，同理，如果右边没有k个人，那么从均可满足。
 
     因为m很大，所以需要离散化处理，先对所有人的彩票数字进行排序，然后对于每个相邻数字区间内，会发现除了最左边的和最左边的第二个位置可能会不一样，其他所有位置都一样，所以只需要判断两个位置即可。
 
        代码：
 
#include #define forr(i, n) for (int i = 0; i < n; i++)
#define FOREACH(iter, coll) for (auto iter = coll.begin(); iter != coll.end(); ++iter)
#define FOREACHR(iter, coll) for (auto iter = coll.rbegin(); iter != coll.rend(); ++iter)
#define lbound(P, K, FUN) ({auto SSS=P, PPP = P-1, KKK=(K)+1; while(PPP+1!=KKK) {SSS = (PPP+(KKK-PPP)/2); if(FUN(SSS)) KKK = SSS; else PPP = SSS;} PPP; })
#define testy()    \int _tests;    \cin >> _tests; \FOR(_test, 1, _tests)
#define CLEAR(tab) memset(tab, 0, sizeof(tab))
#define CONTAIN(el, coll) (coll.find(el) != coll.end())
#define FOR(i, a, b) for (int i = a; i <= b; i++)
#define FORD(i, a, b) for (int i = a; i >= b; i--)
#define MP make_pair
#define PB push_back
#define ff first
#define ss second
#define deb(X) X;
#define SIZE(coll) ((int)coll.size())#define M 1000000007
#define INF 1000000007LLusing namespace std;long long n, m, k;
long long poz_l, poz_p;
vector v;long long policz_ile(long long strzal)
{while (poz_l < n && v[poz_l] < strzal)poz_l++;while (poz_p < n && v[poz_p] <= strzal)poz_p++;long long pocz = poz_p < k ? 0 : (strzal + v[poz_p - k]) / 2 + 1;long long kon = poz_l + k - 1 >= n ? m : (v[poz_l + k - 1] + strzal - 1) / 2;return max(0ll, kon - pocz + 1);
}int solve()
{cin >> n >> m >> k;long long a;forr(i, n){cin >> a;v.PB(a);}sort(v.begin(), v.end());v.PB(m + 1);long long res = policz_ile(0), best = 0;forr(i, n){long long pocz = i == 0 ? max(0ll, v[i] - 2) : max(v[i] - 2, v[i - 1] + 3);long long kon = min(m, v[i] + 2);for (long long s = pocz; s <= kon; s++){long long ile = policz_ile(s);if (ile > res){res = ile;best = s;}}}cout << res << " " << best << '\n';return 0;
}int main()
{std::ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);solve();return 0;
}
 
                        

                        

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！