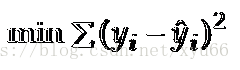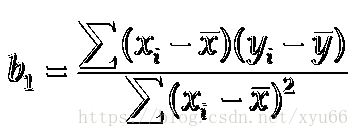线性回归学习笔记

分类：分类(Classification): Y变量为类别型(categorical variable)。如：颜色类别，电脑品牌，有无信誉

回归：回归(regression) Y变量为连续数值型(continuous numerical variable)。如：房价，人数，降雨量

一、简单线性回归模型

1.1简单线性回归模型:

y = β0+β1x +ε  （β0、β1为参数，ε为偏差）>>>>左右求期望值，其中ε偏差为随机变量，均值为0

>>>>得到简单线性回归方程：E(y) = β0+β1x

1.2估计的简单线性回归方程

   ŷ=b0+b1x>>>>>b0和b1是β0和β1的估计值

偏差满足：1.随机变量，均值为0 ；2. ε的方差(variance)对于所有的自变量x是一样的； 3. ε的值是独立的 ；4. ε满足正态分布

2.1.如何练处适合简单线性回归模型的最佳回归线？

如何练处适合简单线性回归模型的最佳回归线？

使sum of squares最小

2.2.计算

例子：x：1、3、2、1、3       均值为2

          y：14、24、18、17、27    均值为20

得到b1 = 20/4  =5   b0 = 20 - 5*2 = 20 - 10 = 10

得到估计的简单线性回归方程  ŷ=b0+b1x=10+5x

2.3. python实现：

import numpy as npdef fitslr(x, y):n = len(x)dinominator = 0;numerator = 0for i in range(0, n):numerator += (x[i] - np.mean(x))* (y[i]  - np.mean(y))dinominator += (x[i] - np.mean(x))**2print("numrator = %.2f" % numerator)print("dimominator = %.2f" % dinominator)b1 = numerator / (dinominator)b0 = np.mean(y) - b1 * np.mean(x)return b0, b1def predict(x, b0, b1):return b0 + x * b1x = [1, 3, 2, 1, 3]
y = [14, 24, 18, 17, 27]b0, b1 = fitslr(x, y)print("intercept =:%.2f slope =: %.2f" %(b0, b1))x_test = 6
y_test = predict(x_test, b0, b1)
print("y_test:%.2f" % y_test)

二、多元线性回归模型（MultipleRegression）

1. 多元回归模型
     y=β0＋β1*x1+β2*x2+ ... +βp*xp+ε
    其中：β0，β１，β2... βp是参数，ε是误差值

2. 多元回归方程
     E(y)=β0＋β１x1+β2x2+ ... +βpxp

3. 估计多元回归方程:
     y_hat=b0＋b1*x1+b2*x2+ ... +bp*xp
    一个样本被用来计算β0，β1，β2... βp的点估计b0, b1, b2,..., bp

4. 估计方法

    使sum of squares最小   

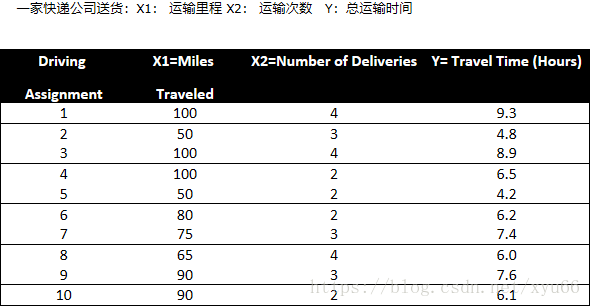
Time = b0+ b1*Miles + b2 * Deliveries

5. Python代码：

from numpy import genfromtxt
import numpy as np
from sklearn import datasets, linear_modeldataPath = r"...\Delivery.csv"
deliveryData = genfromtxt(dataPath, delimiter=',')   # 将以逗号为分隔符的文本文件中导入数据，转化成numpyarray的格式# print("data\n",deliveryData)X = deliveryData[:, :-1]        # 前两列
Y = deliveryData[:,2 ]          # 第三列print("X\n", X)
print("Y\n", Y)regr = linear_model.LinearRegression()  # 调用sklearn的LinearRegression方法regr.fit(X, Y)          # 用.fit方法建立模型print("coefficients: ", regr.coef_)         # b1 b2的估计值
print("intercept: ", regr.intercept_)       # 截距b0的估计值xPredict = [[102, 6]]yPredict = regr.predict(xPredict)print("predicted: ", yPredict)

得到：

coefficients:  [0.0611346  0.92342537]
intercept:  -0.868701466781709
predicted:  [10.90757981]

Time = -0.869 + 0.0611 Miles + 0.923 Deliveries

6. 描述参数含义
     b0: 平均每多运送一英里，运输时间延长0.0611 小时
     b1: 平均每多一次运输，运输时间延长 0.923 小时

     Time = -0.869 +0.0611 *102+ 0.923 * 6
              = 10.9 (小时）

7. 误差ε

 误差ε是一个随机变量，均值为0，ε的方差对于所有的自变量来说相等，所有ε的值是独立的，ε满足正态分布，并且通过β0＋β１x1+β2x2+ ... +βpxp反映y的期望值。

 

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！