python写算法动态规划-高抛低吸-完全背包问题

python写算法动态规划-高抛低吸-完全背包问题

一、关键：

1、完全背包。

把今天与明天各物品的价格差作为物品的价值，物品的原本价格看作物品的体积，转化为了完全背包问题，一共有n天，做n - 1次完全背包问题即可。
！！一点细节，第二天大于第一天才规划，省时间。

2、转化的关键。

首先很重要的一点就是，物品可以当日购买，当日出售。所以：可以把第一天购买第四天才卖的商品看作第二天出售再购买，第三天出售再购买直到第四天出售不购买，赚的钱是一样多的。
！！所以基于上面的思路，不需要考虑隔天的销售情况，我们只需要考虑第二天的售买情况即可。

3、贪心。

完全背包可以让每天都赚到最大，那么到第n天的一定是最多的。

二、题目如下：
纪念品，预测，洛谷p5662

三、代码
1、怎么说呢，我尽力了，也超时了。。。。。

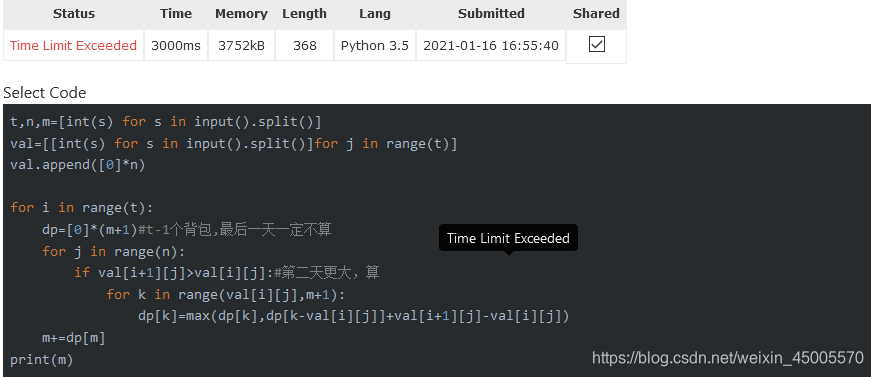
t,n,m=[int(s) for s in input().split()]
val=[[int(s) for s in input().split()]for j in range(t)]
val.append([0]*n)for i in range(t):dp=[0]*(m+1)#t-1个背包,最后一天一定不算for j in range(n):if val[i+1][j]>val[i][j]:#第二天更大，算for k in range(val[i][j],m+1):dp[k]=max(dp[k],dp[k-val[i][j]]+val[i+1][j]-val[i][j])m+=dp[m]
print(m)

2、用c++吧。

#include 
#include using namespace std;const int N = 105, M = 10005;int w[N][N];
int f[M];
int t, n, m;int main()
{scanf("%d%d%d", &t, &n, &m);for (int i = 1; i <= t; i ++ )for (int j = 1; j <= n; j ++ )scanf("%d", &w[i][j]);for (int i = 1; i < t; i ++ ){memset(f, 0, sizeof f);//每次做dp前归零数组for (int j = 1; j <= n; j ++ )if (w[i + 1][j] > w[i][j])  //优化for (int k = w[i][j]; k <= m; k ++ )f[k] = max(f[k], f[k - w[i][j]] + w[i + 1][j] - w[i][j]);//优化后的完全背包模板m += f[m];}printf("%d\n", m);return 0;
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！