局部路径规划：五次多项式

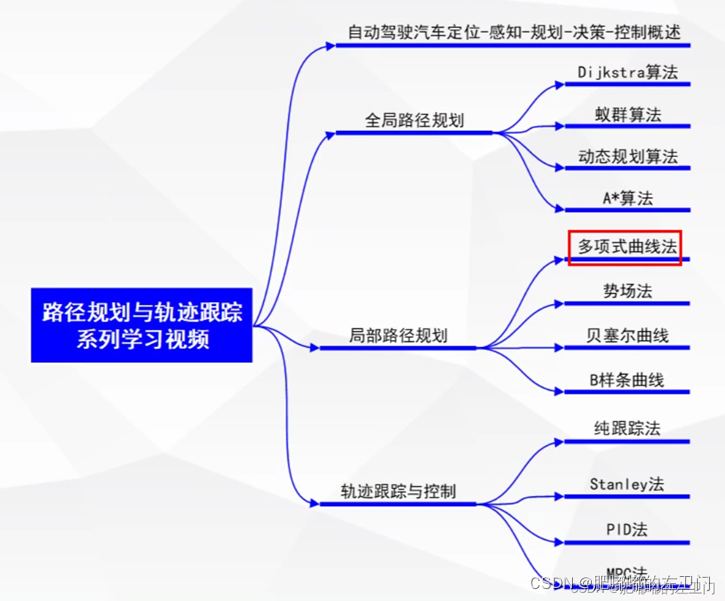
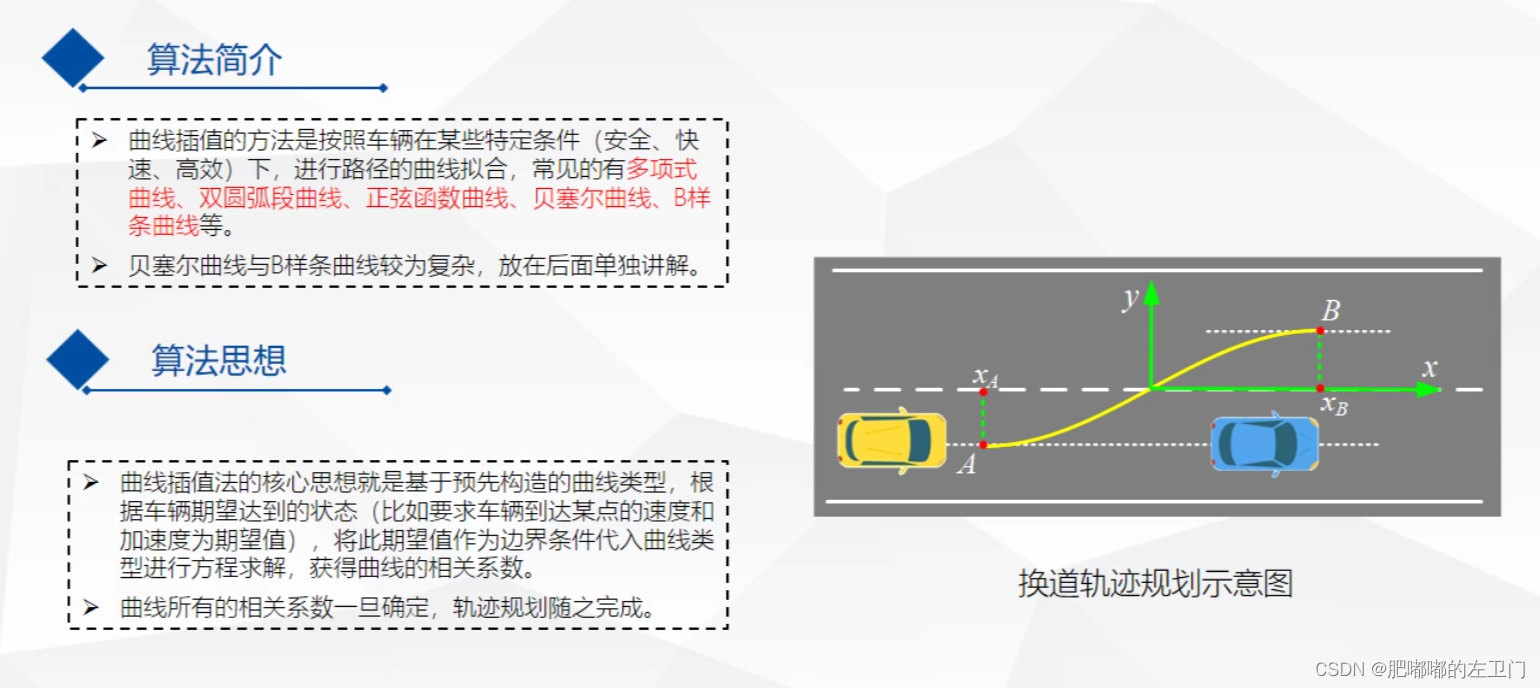
重点注意：进行曲线插值时，分2步：

1，确定所用的曲线类型，即确定曲线的表达式方程，比如多项式曲线，双圆弧段曲线，正弦函数曲线，贝塞尔曲线，B样条曲线等。

2，用现有点的已知条件（位置，速度，加速度等）求解曲线的未知系数，一旦未知系数确定，则曲线的表达式就唯一的确定了。

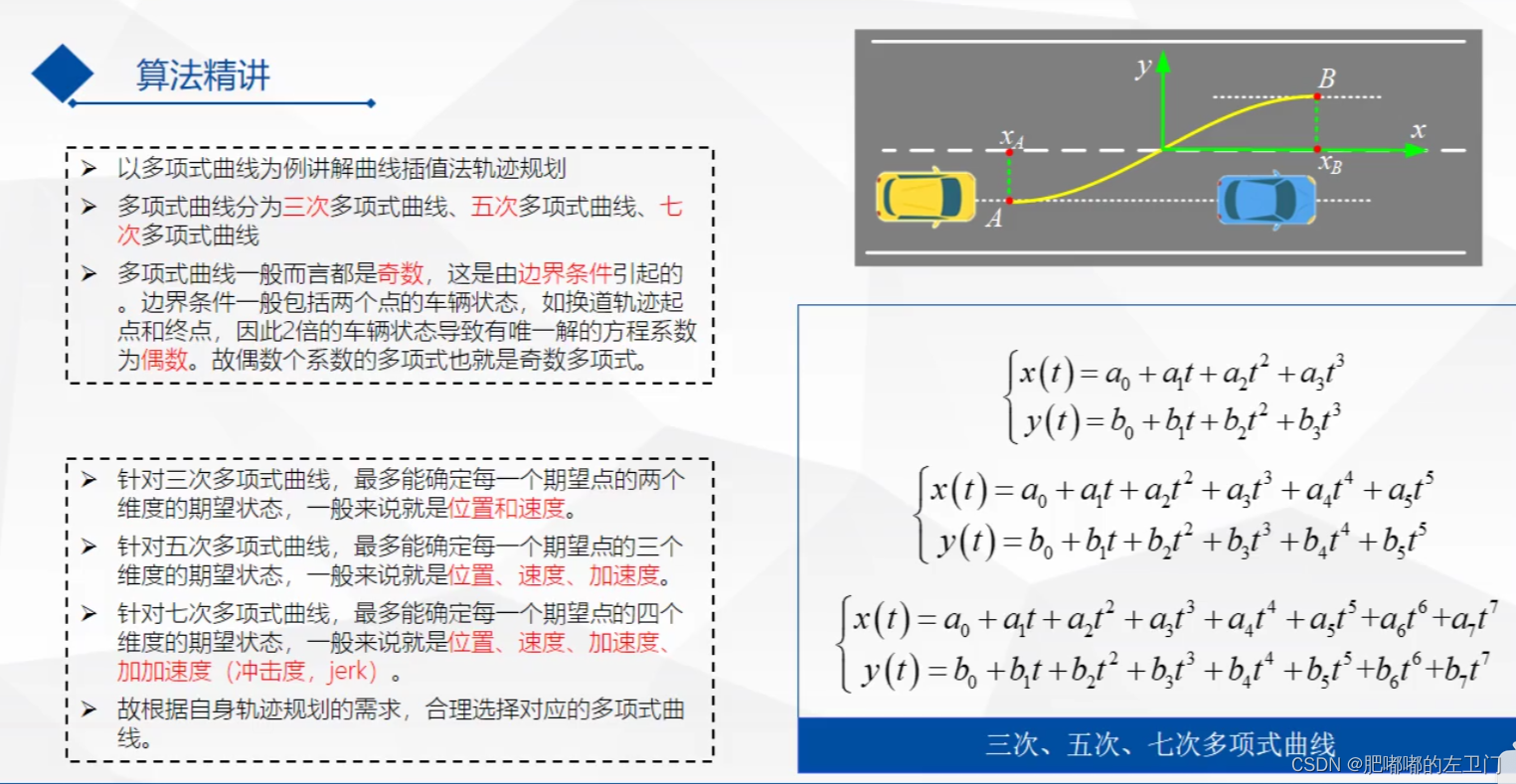
以换道场景为例，曲线是x与y分别关于t的五次多项式，而不是笛卡尔坐标系下y关于x的五次多项式（可参考文章：https://blog.csdn.net/ChenGuiGan/article/details/123072922），故生成的轨迹含有t，所以一旦路径生成了，对应的速度也就生成并确定了，即路径和速度规划是强耦合的。但笛卡尔坐标系下的五次曲线，因为没有t，故仅仅是路径规划，后期需要重新设计速度规划，故实现了路径和速度规划的解耦，优先推荐此方法：

横纵向解耦分别进行规划的方法：

横向和纵向分别用多项式曲线进行分别规划，即横纵向分别对应着2个不同的多项式曲线，然后根据时间t进行合并即可得到横纵向联合控制的曲线，即最终规划的曲线。

！！！重点且易错点一定注意：横向Y和纵向X分别是关于t的五次多项式，但最终合并的曲线Y不是关于X的五次多项式，即最终的曲线不是五次多项式，而是横纵向五次多项式的融合结果。

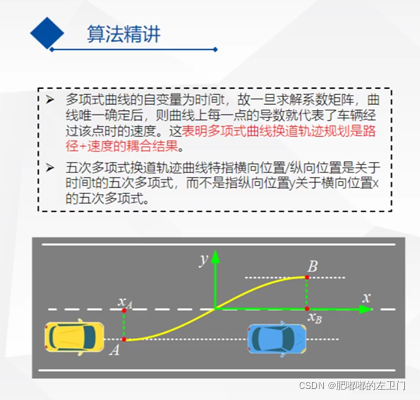
多项式曲线规划的特点：路径和速度是强耦合关系，路径求导就是速度。

问题：速度的方向是如何确定的？？？横纵向方向的矢量和就是最终的速度方向。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！