realme 拨号代码_九章算法 | 微软面试题：骑士拨号器

国际象棋中的骑士可以按下图所示进行移动：

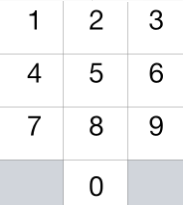
这一次，我们将 “骑士” 放在电话拨号盘的任意数字键（如上图所示）上，接下来，骑士将会跳 N-1 步。每一步必须是从一个数字键跳到另一个数字键。

每当它落在一个键上（包括骑士的初始位置），都会拨出键所对应的数字，总共按下 N位数字。

你能用这种方式拨出多少个不同的号码？

因为答案可能很大，所以输出答案模 10^9 + 7。

1≤N≤5000

在线评测地址: LintCode 领扣

样例 1：

输入：1
输出：10
说明：
答案可能是0,1,2,3, ... , 9，

样例 2：

输入：2
输出：20
说明：
答案可能是04, 06, 16, 18, 27, 29, 34, 38, 43, 49, 40, 61, 67, 60, 72, 76, 81, 83, 94, 92。

样例 3：

输入：3
输出：46

【题解】

本题采用动态规划的方法，考虑每一步棋子变化的状态，进行统计。我们可以使用滚动数组节省空间。

class Solution {public int knightDialer(int N) {int MOD = 1_000_000_007;int[][] moves = new int[][]{{4,6},{6,8},{7,9},{4,8},{3,9,0},{},{1,7,0},{2,6},{1,3},{2,4}};int[][] dp = new int[2][10];Arrays.fill(dp[0], 1);for (int hops = 0; hops < N-1; ++hops) {Arrays.fill(dp[~hops & 1], 0);for (int node = 0; node < 10; ++node)for (int nei: moves[node]) {dp[~hops & 1][nei] += dp[hops & 1][node];dp[~hops & 1][nei] %= MOD;}}long ans = 0;for (int x: dp[~N & 1])ans += x;return (int) (ans % MOD);}

更多语言代码参见：九章算法

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！