机器学习之二（读书笔记）

四、Gradient Descent（梯度下降）

θ ∗ = a r g m i n θ L ( θ ) \theta ^{\ast } = arg\underset{\theta}{min } L(\theta ) θ∗=argθmin​L(θ)
L:loss function
$\theta$:parameters
梯度下降步骤：
1.选取两个参数{ θ 1 , θ 2 \theta_{1},\theta _{2} θ1​,θ2​}
2.随意选取一个初始位置 θ 0 = [ θ 1 0 θ 2 0 ] \theta^{0} = \begin{bmatrix} \theta _{1}^{0}\\ \theta _{2}^{0} \end{bmatrix} θ0=[θ10​θ20​​]
3.通过梯度下降得到新的位置 θ 1 \theta^{1} θ1，即
[ θ 1 1 θ 2 1 ] = [ θ 1 0 θ 2 0 ] − η [ ∂ L ( θ 1 0 ) / ∂ θ 1 ∂ L ( θ 2 0 ) / ∂ θ 2 ] \begin{bmatrix} \theta _{1}^{1}\\ \theta _{2}^{1} \end{bmatrix} = \begin{bmatrix} \theta _{1}^{0}\\ \theta _{2}^{0} \end{bmatrix} - \eta \begin{bmatrix} \partial L(\theta _{1}^{0})/\partial\theta _{1}\\ \partial L(\theta _{2}^{0})/\partial\theta _{2} \end{bmatrix} [θ11​θ21​​]=[θ10​θ20​​]−η[∂L(θ10​)/∂θ1​∂L(θ20​)/∂θ2​​]，其中$\eta$为learning rate，后面为对Loss function的偏微分；
4.同样的步骤得到 θ 2 \theta^{2} θ2、 θ 3 \theta^{3} θ3… θ n \theta^{n} θn
[ θ 1 2 θ 2 2 ] = [ θ 1 1 θ 2 1 ] − η [ ∂ L ( θ 1 1 ) / ∂ θ 1 ∂ L ( θ 2 1 ) / ∂ θ 2 ] \begin{bmatrix} \theta _{1}^{2}\\ \theta _{2}^{2} \end{bmatrix} = \begin{bmatrix} \theta _{1}^{1}\\ \theta _{2}^{1} \end{bmatrix} - \eta \begin{bmatrix} \partial L(\theta _{1}^{1})/\partial\theta _{1}\\ \partial L(\theta _{2}^{1})/\partial\theta _{2} \end{bmatrix} [θ12​θ22​​]=[θ11​θ21​​]−η[∂L(θ11​)/∂θ1​∂L(θ21​)/∂θ2​​]
…
Gradient（一个vector）： ▽ L ( θ ) = [ ∂ L ( θ 1 ) / ∂ θ 1 ∂ L ( θ 2 ) / ∂ θ 2 ] \triangledown L(\theta ) = \begin{bmatrix} \partial L(\theta_{1} )/\partial \theta _{1}\\ \partial L(\theta_{2})/\partial \theta _{2} \end{bmatrix} ▽L(θ)=[∂L(θ1​)/∂θ1​∂L(θ2​)/∂θ2​​]
则 θ 1 = θ 0 − η ▽ L ( θ 0 ) \theta ^{1} = \theta ^{0} - \eta \triangledown L(\theta ^{0}) θ1=θ0−η▽L(θ0)，以此类推。

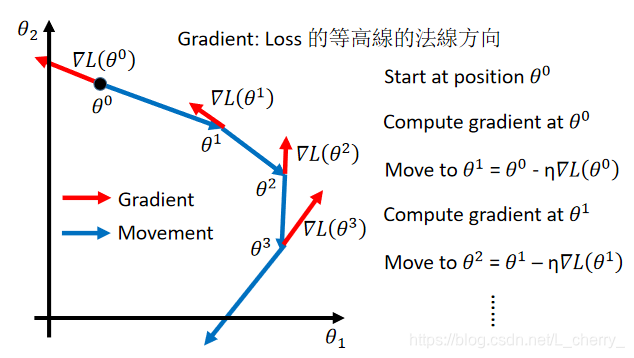
***Granient Descent tips:
Tip 1:Tuning your learning rates
  learning rate 的大小会影响loss，如果参数过多没办法直接可视化loss function，这个时候可以画出不同learning rate对update loss时loss的变化：（常用框架里有自动调整的方法，参考ReduceLROnPlateau）

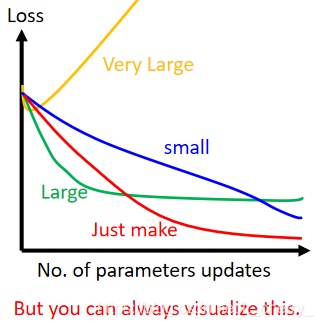
不同的参数应该给不同的learning rate
  有一些自动的方法可以帮助我们调learning rate：

   Adagrad（自适应梯度算法）
每一个参数的learning rate都让它除上之前算出来的微分值的root mean square（均方根）。
传统的Gradient Descent 和Adagrad对比：

  其中， σ t \sigma ^{t} σt是过去所有偏微分g的值的root mean square（均方根）。
具体操作：
  假设 w 0 w ^{0} w0的那点的微分是 g 0 g^{0} g0，它的learning rate是 η 0 / σ 0 \eta ^{0}/\sigma^{0} η0/σ0， σ 0 \sigma^{0} σ0是过去所有微分值的root mean square，即 ( g 0 ) 2 \sqrt{(g^{0})^{2}} (g0)2 ​，以此类推，如下图：

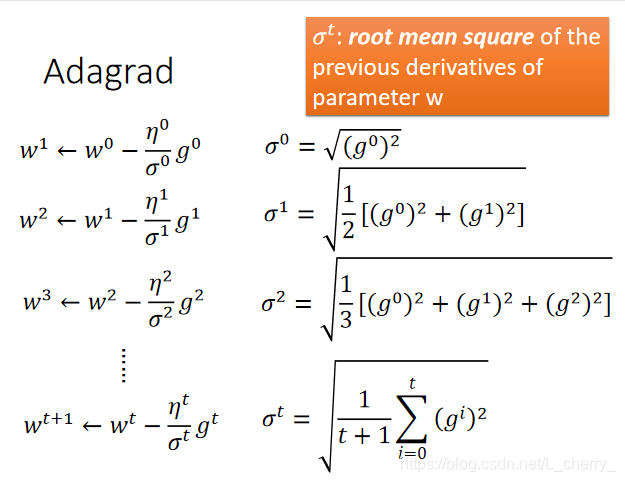
总结一下Adargad式子：

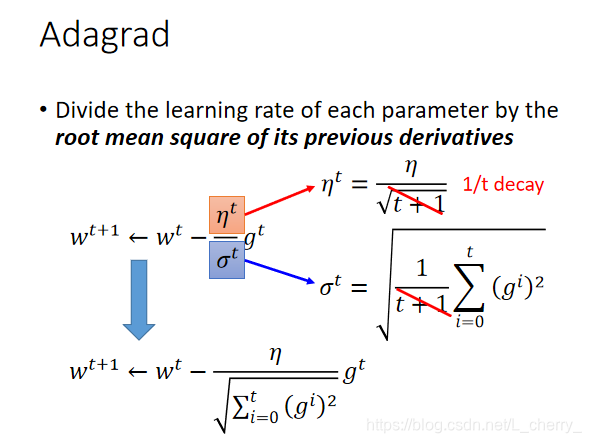
  使用Adargad方法都后期会update越来越慢，慢到令人发指，还有别的方法比如Adam方法，是最稳定的。

  疑问？在梯度下降中Gradient越大，update越快，但是使用Adagrad时，微分值越大，分子g表示update越快，分母却使update步伐越小（解释说，分母是为了造成反差的效果）。可看作 一次微分/二次微分， g t g^{t} gt一次微分，下面的分母可看作二次微分（一般在使用Adagrad时计算二次微分会比较复杂，我们可用一次微分去估计二次微分，即取几个点计算 ( f i r s t d e r i v a t i v e ) 2 \sqrt{(firstderivative)^{2}} (firstderivative)2 ​）

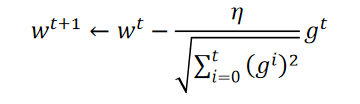
**Tip 2：Stochastic Gradient Descent （随机梯度下降法）
make the training faster
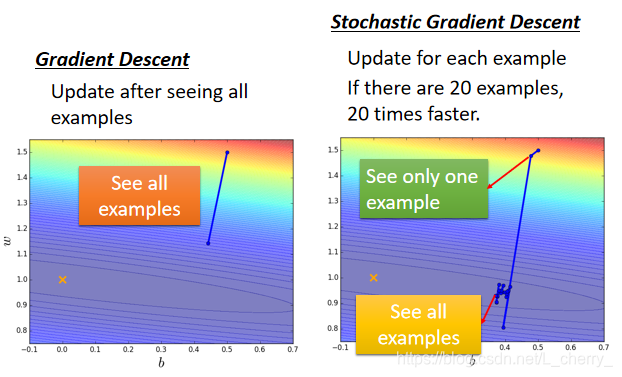
  以Regression的Loss function为例Gradient Descent的做法（计算所有的loss然后才update参数）：

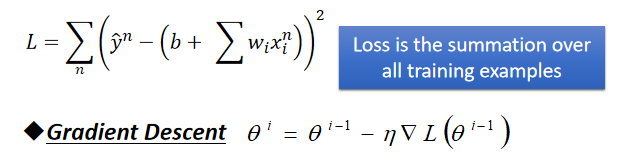
Stochastic Gradient Descent 的做法：

1.随机选取（也可按顺序选取）一个example x n x^{n} xn
2.计算（某一个example的）loss：
L n = ( y ^ n − ( b + ∑ w i x i n ) ) 2 L^{n} = (\hat{y}^{n} - (b + \sum w_{i}x_{i}^{n}))^{2} Ln=(y^​n−(b+∑wi​xin​))2
3.计算对某一个example，它的loss的Gradient，再update参数：
θ i = θ i − 1 − η ▽ L n ( θ i − 1 ) \theta ^{i} = \theta ^{i - 1} - \eta \triangledown L^{n}(\theta ^{i - 1} ) θi=θi−1−η▽Ln(θi−1)

**Tip 3：Feature Scaling（特征缩放）
  以Regression为例：
   y = b + w 1 x 1 + w 2 x 2 y = b + w_{1} x_{1}+ w_{2}x_{2} y=b+w1​x1​+w2​x2​中有两个input的feature： x 1 x_{1} x1​和 x 2 x_{2} x2​，我们希望它们分布的range一样，可做scaling（归一化思想）：

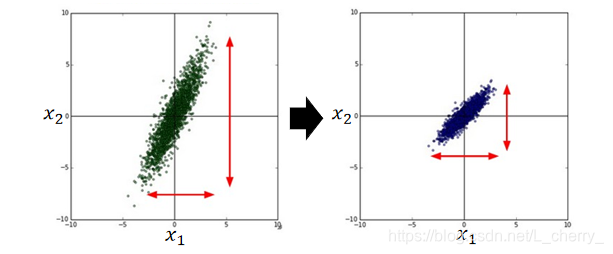
  Feature Scaling的做法（有很多，这是其中一种常见局部化做法）：
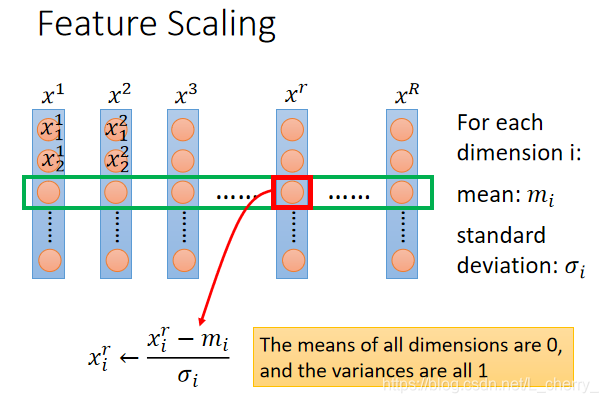
  假设我有r个example， x 1 , x 2 , . . . . . . , x r , . . . . . . x R x^{1},x^{2},......,x^{r},......x^{R} x1,x2,......,xr,......xR，每一笔example里都有一组feature，例如 x 1 x^{1} x1的feature： x 1 1 , x 2 1 . . . . . . x_{1}^{1},x_{2}^{1}...... x11​,x21​......
1.feature scaling 就是对每一个dimension i 计算mean，即 m i m_{i} mi​，和计算它的deviation（偏离），即 σ i \sigma_{i} σi​；
2.然后对r个example的第i个component减掉所有data的第i个component的mean，再除掉所有data的第i个component的standard deviation；
3.做完以上，所有的dimension的mean就会为0，而variance就会是1

Formal Derivation：
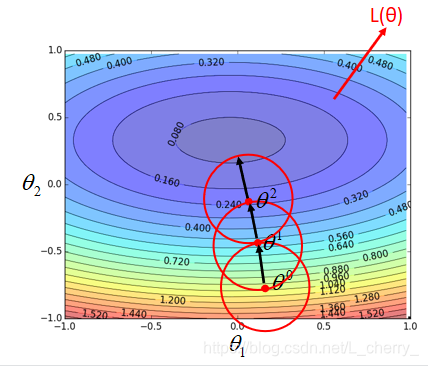
  取一个点，再取以这个点为圆心的圆，选择这个圆的最低点作为下一个点，以此类推…

补充知识点：
Taylor Series
  任何一个function h(x)，如果它在 x = x 0 x = x_{0} x=x0​这一点是infinitely differentiable（无限可微），那么可把h(x)写成：
h ( x ) = ∑ k = 0 ∞ h ( k ) ( x 0 ) k ! ( x − x 0 ) k h(x) = \sum_{k = 0}^{\infty }\frac{h^{(k)}(x_0)}{k!}(x-x_0)^{k} h(x)=k=0∑∞​k!h(k)(x0​)​(x−x0​)k

= h ( x 0 ) + h ′ ( x 0 ) ( x − x 0 ) + h ′ ′ ( x 0 ) 2 ! ( x − x 0 ) 2 + . . . =h(x_0) +{h}'(x_0)(x-x_0)+\frac{{h}''(x_0)}{2!}(x-x_0)^{2}+... =h(x0​)+h′(x0​)(x−x0​)+2!h′′(x0​)​(x−x0​)2+...
  当x接近 x 0 x_0 x0​时以上可写成：
h ( x ) ≈ h ( x 0 ) + h ′ ( x 0 ) ( x − x 0 ) h(x)\approx h(x_0) +{h}'(x_0)(x-x_0) h(x)≈h(x0​)+h′(x0​)(x−x0​)
  以上只考虑一个variable，如果考虑好几个参数，即Multivariable Taylor Series:
h ( x , y ) ≈ h ( x 0 , y 0 ) + ∂ h ( x 0 , y 0 ) ∂ x ( x − x 0 ) + ∂ h ( x 0 , y 0 ) ∂ y ( y − y 0 ) h(x,y)\approx h(x_0,y_0) +\frac{\partial h(x_0,y_0)}{\partial x}(x-x_0)+\frac{\partial h(x_0,y_0)}{\partial y}(y-y_0) h(x,y)≈h(x0​,y0​)+∂x∂h(x0​,y0​)​(x−x0​)+∂y∂h(x0​,y0​)​(y−y0​)

  根据Multivariable Taylor Series改写loss function：
L ( θ ) ≈ L ( a , b ) + ∂ L ( a , b ) ∂ θ 1 ( θ 1 − a ) + ∂ L ( a , b ) ∂ θ 2 ( θ 2 − b ) L(\theta ) \approx L(a,b) + \frac{\partial L(a,b)}{\partial \theta _1}(\theta _1-a)+ \frac{\partial L(a,b)}{\partial \theta _2}(\theta _2-b) L(θ)≈L(a,b)+∂θ1​∂L(a,b)​(θ1​−a)+∂θ2​∂L(a,b)​(θ2​−b)
其中s,u,v都是常数，化简为：

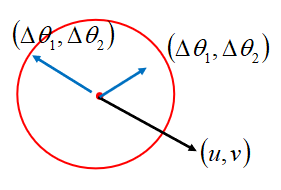
  为了让$L(\theta )$最小，应该让 ( Δ θ 1 , Δ θ 2 ) (\Delta \theta _1,\Delta \theta _2) (Δθ1​,Δθ2​)与(u,v)反向并成正比，即：

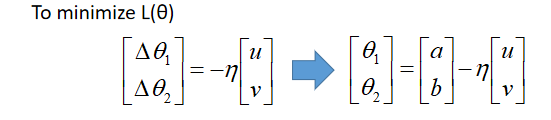
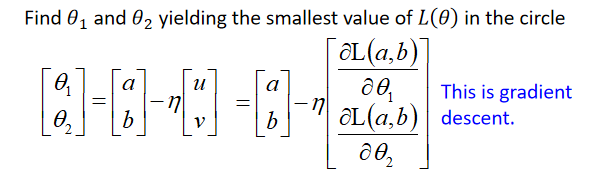
  以上验证了gradient descent。

Gradient Descent的限制
a.会卡在local minimum的位置；
b.也可能会卡在不是local minimum的位置，比如saddle point（鞍点），此时的微分也为0；
c.也有可能卡在微分值很小接近于0的位置，此时可能在高原位置

本文是对blibli上李宏毅机器学习2020的总结，如有侵权会立马删除。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！