打开神经网络的黑箱（二） 多层感知机（MLP）的空间划分与编码逻辑

概述

上一篇文章 解析了单层全连接分类模型的（输入）空间划分（Space Partitioning）与编码逻辑或数学原理，这篇文章将主要是解析多层感知机（Multi-Layer Perceptron，MLP）或多层全连接层构成的模型的空间划分与编码逻辑。多层感知机与单层全连接分类模型较大的区别在于，隐藏层的空间划分与编码并不遵循理想情况下使得每一个线性区域（Linear Regions）只包含单个类别的数据这样的逻辑，所以会复杂一些，基础的空间划分与编码逻辑可参考上一篇文章，本文将不再赘述。

多层感知机

在多层感知机中，最简单的模型是二层感知机模型（不含输入层），即只含有单层隐藏层的感知机模型。这种二层模型在深度学习风靡之前被广泛研究，尤其是万能近似定理（Universal Approximation Theorem）证明了含有一层或多层隐藏层的神经网络可以以任意的精度近似任何从一个有限维空间到另一个有限维空间的Borel可测函数。

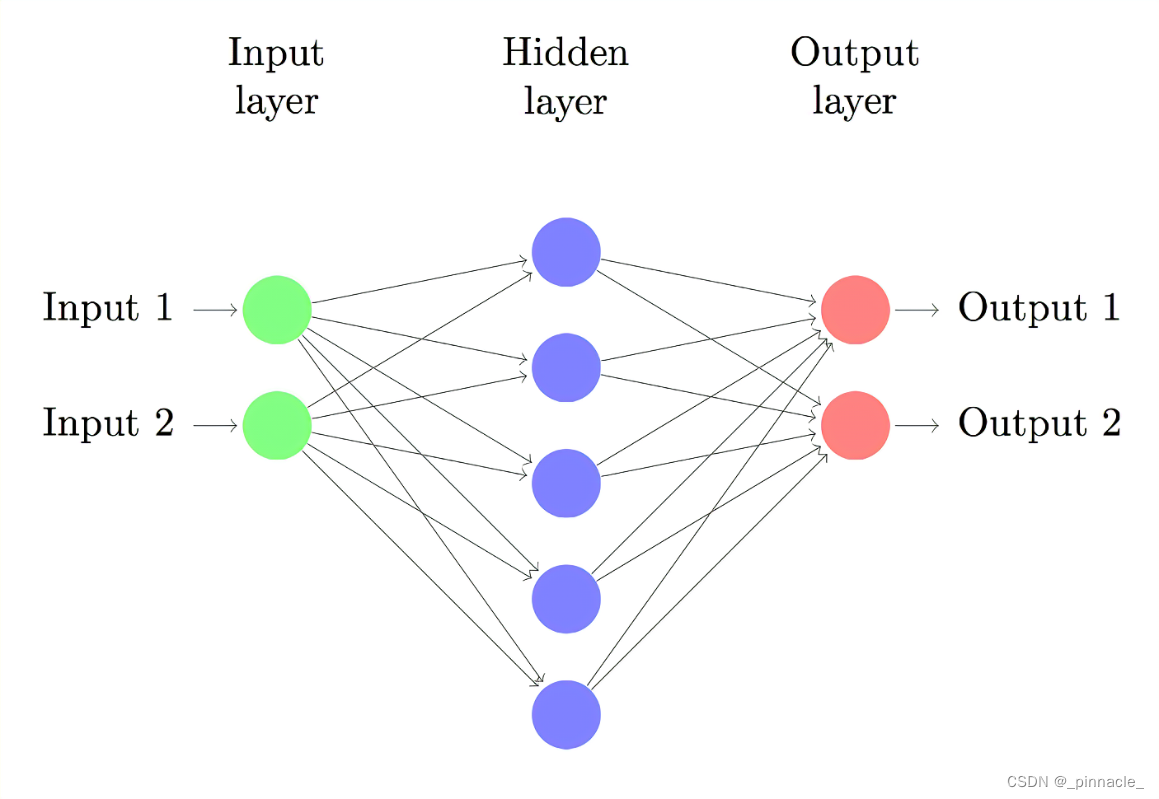
而在多层感知机模型中，因为隐藏层的存在，使得其模型运行逻辑变得和无隐藏层模型异常的不同，很难沿用无隐藏层模型的分析逻辑，这个也是深度神经网络难以被研究的原因之一。本文主要解析$2$个输出节点的模型，即二分类模型；而多分类模型都可以通过One-vs-Rest策略转化为二分类模型，所以分析多分类模型意义有限，当然本身多分类+隐藏层也会加剧分析的难度。隐藏层的激活函数统一使用$ReLU(x)$，在很多深度学习理论研究的论文中都是以$ReLU(x)$函数作为基础的，在神经网络理论研究中有重要的地位。

从前面无隐藏层的分析中我们也知道，两个输出节点无非构造了一个分离超平面，就是不管隐藏层如何映射，我们都在输出这一层切一刀下去将两个类别分离。换句话说就是要求经过隐藏层映射的数据必须是线性可分的。下面将解析如图所示的单隐藏层的模型，并推广到含多隐藏层的模型上。

单隐藏层模型

我们知道隐藏层单一节点的输出为 y = R e L U ( w T x + b y=ReLU(w^Tx+b y=ReLU(wTx+b)，因为ReLU激活函数的作用， w T x + b = 0 w^Tx+b=0 wTx+b=0直接显式的构成分离超平面(证明可以看这里)，将输入空间一分为二，即 x − , x + x^-,x^+ x−,x+。
y = { 0 , x ⊆ x − w T x + b , x ⊆ x + y=\left\{\begin{matrix} 0&,x\subseteq x^-\\ w^Tx+b&,x\subseteq x^+ \end{matrix}\right. y={0wTx+b​,x⊆x−,x⊆x+​对于任意的单隐藏层分类网络（这里主要理解二分类的情形），都可以写成：
F ( x ; θ ) = w 2 T R e L U ( w 1 T x + b 1 ) + b 2 F(x;\theta)=w_2^TReLU(w_1^Tx+b_1)+b_2 F(x;θ)=w2T​ReLU(w1T​x+b1​)+b2​在上一章我们主要研究决策超平面，在这章也会延续这个思路，那么对于单隐藏层网络而言它的决策超平面是什么呢？在上一章讲了二分类转回归的方法，即将 w 1 = [ w 2 0 , w 2 1 ] T w_1=[w_{2}^0,w_2^1]^T w1​=[w20​,w21​]T作一次代数替换 w r = [ w 2 0 − w 2 1 ] w_r=[w_{2}^0-w_2^1] wr​=[w20​−w21​]，同理 b r = b 2 0 − b 2 1 b_r=b_2^0-b_2^1 br​=b20​−b21​，这个时候就变成回归问题了，即：
F r ( x ; θ ) = w r T R e L U ( w 1 T x + b 1 ) + b r F_r(x;\theta)=w_r^TReLU(w_1^Tx+b_1)+b_r Fr​(x;θ)=wrT​ReLU(w1T​x+b1​)+br​单隐藏层网络的决策超平面就变为：
H = { x ∣ w r T R e L U ( w 1 T x + b 1 ) + b r = 0 } H=\{x \mid w_r^TReLU(w_1^Tx+b_1)+b_r = 0\} H={x∣wrT​ReLU(w1T​x+b1​)+br​=0}需要说明的是，这个超平面和我们理解的线性超平面不同，它不再是简单的线性了，而是分段线性函数（Piecewise Linear Function）或分段超平面所组成的决策面，如图：

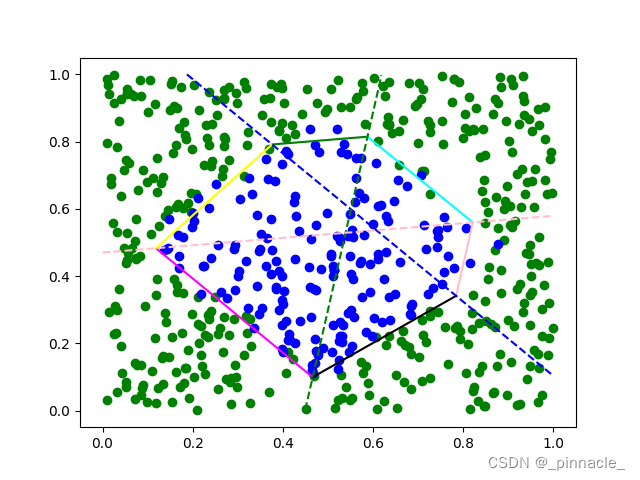
模型训练后，实线线段所组成的六边形即是单隐藏层网络（3个隐藏节点）所构成的决策面；而虚线表示隐藏层每个节点的节点超平面，这里隐藏层将输入空间划分为7个线性区域（Linear Regions），整个模型将输入空间划分为13个线性区域。

大家肯定比较疑惑这个分段线性函数从何而来，为什么由单一隐藏层构成的网络产生的决策超平面和无隐藏层的模型完全不同了，居然是封闭的多个线性分段函数构成的决策面。这个问题也是我们接下来要研究的问题之一。

激活函数$ReLU$能直接将节点超平面转化为分离超平面，只不过在这里隐藏层的分离超平面并不直接的对数据分类，而是多个分离超平面构成的超平面编排（Hyperplane Arrangement）将输入空间$R$划分为$k$个线性区域（这里$R$特指$n$维度实数空间 R n R^n Rn，下同）。如上图虚线隐藏层分离超平面将输入空间划分为7个线性区域。

对于任意线性区域，当神经网络训练完成，权值固定下来后，其编码就被确定下来，比如，假设隐藏层所划分的某一线性区域 R l k ⊆ R R^k_{l}\subseteq R Rlk​⊆R，其中$R$为输入空间， R l k R^k_{l} Rlk​为第$l$隐藏层划分后的第$k$个线性区域（这里只有一个隐藏层，默认$l=1$），定义 R l k R^k_{l} Rlk​的区域编码为 E l k E^k_{l} Elk​，如 E l k = [ 1 , 1 , 0 ] E^k_{l}=[1,1,0] Elk​=[1,1,0]，且 x ∈ R l k x\in R^k_{l} x∈Rlk​，我们可以将 E l k E^k_{l} Elk​转换为对角矩阵即：
D l k = D i a g ( E l k ) = [ 1 1 0 ] D^k_{l}=Diag(E^k_{l})=\begin{bmatrix} 1& & \\ & 1& \\ & & 0 \\ \end{bmatrix} Dlk​=Diag(Elk​)= ​1​1​0​ ​ 对于任意隐藏节点，$ReLU$可以表示为如下形式：
R e L U ( w T x + b ) = { 1 ∗ ( w T x + b ) , w T x + b > 0 0 ∗ ( w T x + b ) , w T x + b ≤ 0 ReLU(w^Tx+b)=\left\{\begin{matrix} 1*(w^Tx+b)&,w^Tx+b>0\\ 0*(w^Tx+b)&,w^Tx+b\leq0 \end{matrix}\right. ReLU(wTx+b)={1∗(wTx+b)0∗(wTx+b)​,wTx+b>0,wTx+b≤0​

所以 F r ( x ; θ ) F_r(x;\theta) Fr​(x;θ)可以写为:
F r ( x ; θ ) = w r T ( D l k ( w 1 T x + b 1 ) ) + b r F_r(x;\theta)=w_r^T(D^k_{l}(w_1^Tx+b_1))+b_r Fr​(x;θ)=wrT​(Dlk​(w1T​x+b1​))+br​矩阵乘法满足加法交换律，所以
F r ( x ; θ ) = w r T D l k w 1 T x + w r T D l k b 1 + b r F_r(x;\theta)=w_r^TD^k_{l}w_1^Tx+w_r^TD^k_{l}b_1+b_r Fr​(x;θ)=wrT​Dlk​w1T​x+wrT​Dlk​b1​+br​我们令 w T = w r T D l k w 1 T , b = w r T D l k b 1 + b r w^T=w_r^TD^k_{l}w_1^T,b=w_r^TD^k_{l}b_1+b_r wT=wrT​Dlk​w1T​,b=wrT​Dlk​b1​+br​，可得:
F r ( x ; θ ) = w T x + b F_r(x;\theta)=w^Tx+b Fr​(x;θ)=wTx+b就可以得到在任意线性区域 R l k R^k_{l} Rlk​内的超平面方程：
H = { x ∈ R l k ∣ w T x + b = 0 } H=\{x\in R^k_{l} \mid w^Tx+b=0\} H={x∈Rlk​∣wTx+b=0}这个结果很巧，我们知道单层感知机的超平面方程是：
H = { x ∈ R ∣ w T x + b = 0 } H=\{x\in R \mid w^Tx+b=0\} H={x∈R∣wTx+b=0}所以两者存在等价形式的决策超平面，二层网络和单层网络的区别是输入空间约束，对于二层网络而言，第二层的线性区域划分是建立在第一层划分的线性区域约束上的。同理，我们可以推理出多层网络（不含跨层连接，skip connection）的线性区域划分逻辑是：后一层递归的在前一层所划分的线性区域内再次划分输入空间。
左图实线为3个隐藏节点的单隐藏层感知机，在任意虚线划分的线性区域 R l k R^k_{l} Rlk​内的决策超平面（未限制输入空间范围）；红色实线是属于中心三角区(区域编码： E l k = [ 1 , 1 , 1 ] E^k_{l}=[1,1,1] Elk​=[1,1,1])的决策超平面，其所在区域并不在中心三角区，所以是无效的超平面；右图为限制决策超平面在所属 R l k R^k_{l} Rlk​时的分段线性决策面；

不同的区域编码 E l k E^k_{l} Elk​直接改变了超平面方程，这个也是激活函数的作用之一，而输入空间约束则限制了超平面的范围，即所谓线性分段的由来。

需要注意的是：不是每一个线性区域内都有一个超平面，比如在上图中编码为 E l k = [ 1 , 1 , 1 ] E^k_{l}=[1,1,1] Elk​=[1,1,1]的线性区域的超平面方程是存在的，但是该超平面并不在所属区域内，该区域实际上是被其他区域决策超平面所包含了。 E l k = [ 0 , 0 , 0 ] E^k_{l}=[0,0,0] Elk​=[0,0,0]的线性区域也不存在，因为根本不存在这个编码区。

区域切片与映射

上面讲了在原始输入空间$x$上的区域是如何编码与划分的，我们知道分类层所直接划分的数据并不是原始输入空间，而是经过线性变换后的空间，或其直接划分的是隐藏层的数据。
上图中，右边与下边的图都是经过隐藏层映射后输出的数据，且值域不再是$[0,1]$，而是大于等于$0$的无约束数据。我们可以看到原始输入数据$x$被隐藏层映射后，切片到了不同线性区域，分类层通过其区域编码使用不同的权值将隐藏层的数据线性划分。这些分离超平面映射到原始输入数据$x$上，就是左上角图中的分段线性决策边界。

上图中没有画其他线性区域的图，编码区$[0,0,1]，[1,0,0]，[0,1,0]$都是一维的线段，被一个点所划分，而编码区$[1,1,1]$则是三维的数据，被一个平面划分，读者可以通过源代码自己去实践。

多隐藏层模型

本质上说由全连接层与$ReLU$构成的网络层表示了一类函数，而由全连接层与$argmax$构成的网络层表示另一类函数，同类函数的很多性质是通用的，如对输入空间的划分方式是相同的。所以多隐藏层的网络和单隐藏层的网络本质也差不多，区别就是每增加一层隐藏层就会对输入空间的子空间进行最大 ∑ i = 0 d C m i \sum_{i=0}^{d}C_m^i ∑i=0d​Cmi​次划分，其中$d$为输入空间维度；$m$为隐藏层节点数；所以每次划分都会使线性区域变小，数量变多，其带来的结果就是线性分段函数变得更加精细和复杂。
上图为2层隐藏层（每个隐藏层包含3个节点）的可视化结果，红色虚线是第一层隐藏层节点的分离超平面，灰色虚线为第二层隐藏层节点的分离超平面，实线为第三层分类层的分段超平面组成的决策边界。

所以综上，隐藏层由$ReLU$激活函数构成的多层感知机的本质就是：递归的分段线性函数，即递归的使用线性函数在约束空间内划分输入空间。而且我们发现其输入空间划分的逻辑与决策树（decision tree）是完全一致的。
上图左侧为决策树的一个示例，右侧为决策树所划分的输入空间及由分段线性函数所组成的决策边界（决策树的节点划分评价函数为entropy，最大深度为6，划分内部节点的最小样本数为10个）

需要说明的是多层感知机其层内空间划分相关性非常强，原因是其层内存在大量的参数共享，而决策树基本没有这种相关性，所以两者决策边界的选择方式是非常不同的，决策树相对更加自由，而多层感知机则有很大的约束，这也许就是神经网络不容易过拟合的原因，相对的决策树则更容易过拟合。

线性区域数量

理解了多层感知机模型的数学原理与编码逻辑，那么线性区域就很好计算了，对于一个拥有$L$层隐藏层与$1$层全连接层的前馈神经网络模型(无跨层连接)，可以定义其函数 F : R n 0 ⟶ R u F:R^{n^0}\longrightarrow R^{u} F:Rn0⟶Ru 的带参数的形式为：
F ( x ; θ ) = f u h u ∘ g L ∘ f L h L ∘ ⋯ ∘ g 1 ∘ f 1 h 1 ( x ) F(x; \theta) = f_{u}^{h_{u}} \circ g_L \circ f_L^{h_L} \circ \dots \circ g_1 \circ f_1^{h_1}(x) F(x;θ)=fuhu​​∘gL​∘fLhL​​∘⋯∘g1​∘f1h1​​(x)其中 n 0 n^0 n0为初始输入空间的维度，$u$为输出空间的维度，$g$为激活函数，$f$为全连接函数，$h$为输出节点数，其中 h 0 = n 0 h_0=n^0 h0​=n0。而最大线性区域数量公式为：
N ( d , m ) = 1 + m + C m 2 + . . . + C m d = ∑ i = 0 d C m i N(d,m)=1+m+C_m^2+...+C_m^d=\sum_{i=0}^{d}C_m^i N(d,m)=1+m+Cm2​+...+Cmd​=i=0∑d​Cmi​其中$N$，$d$，$m$分别最大线性区域数量，输入空间维度，隐藏节点或超平面数量。

到第$1$层隐藏层，$F(x;\theta )$划分的最大线性区域数量为：
N = N ( n 0 ， h 1 ) = ∑ i = 0 n 0 C h 1 i N=N(n^{0}，h_1)= \sum_{i=0}^{n^{0}}C_{h_1}^i N=N(n0，h1​)=i=0∑n0​Ch1​i​到第$2$层隐藏层，$F(x;\theta )$划分的最大线性区域数量为：
N = N ( n 0 ， h 1 ) ∗ N ( h 1 ， h 2 ) = ∑ i = 0 n 0 C h 1 i ∗ ∑ i = 0 h 1 C h 2 i N=N(n^{0}，h_1)*N(h_1，h_2)= \sum_{i=0}^{n^{0}}C_{h_1}^i * \sum_{i=0}^{h_1}C_{h_2}^i N=N(n0，h1​)∗N(h1​，h2​)=i=0∑n0​Ch1​i​∗i=0∑h1​​Ch2​i​
到第$L$层隐藏层，$F(x;\theta )$划分的最大线性区域数量为：
N = ∏ j = 0 L ∑ i = 0 h j C h j + 1 i N=\prod_{j=0}^{L} \sum_{i=0}^{h_j}C_{h_{j+1}}^i N=j=0∏L​i=0∑hj​​Chj+1​i​到分类层 f u h u f_{u}^{h_{u}} fuhu​​，$F(x;\theta )$划分的最大线性区域数量为，
N = ( ∏ j = 0 L ∑ i = 0 h j C h j + 1 i ) ∑ i = 0 h L C c u 2 i N=(\prod_{j=0}^{L} \sum_{i=0}^{h_j}C_{h_{j+1}}^i)\sum_{i=0}^{h_L}C_{c_u^2}^i N=(j=0∏L​i=0∑hj​​Chj+1​i​)i=0∑hL​​Ccu2​i​

参数共享

这里简单解析多层感知机中的参数共享。我们知道在卷积网络（CNN）中有参数共享的概念，在多层感知机中也是存在的，比如$3$个隐藏节点的单隐藏层二分类模型中，被隐藏层划分的输入空间存在两个线性区域的编码 E l 1 = [ 1 , 1 , 0 ] E^1_{l}=[1,1,0] El1​=[1,1,0]和 E l 2 = [ 1 , 0 , 0 ] E^2_{l}=[1,0,0] El2​=[1,0,0]，其超平面公式可写为：
{ 1 ∗ w 1 x 1 + 1 ∗ w 2 x 2 + 0 ∗ w 3 x 3 + b = 0 1 ∗ w 1 x 1 + 0 ∗ w 2 x 2 + 0 ∗ w 3 x 3 + b = 0 ⇒ { w 1 x 1 + w 2 x 2 + b = 0 w 1 x 1 + b = 0 \left\{\begin{matrix} 1*w_1x_1+1*w_2x_2+0*w_3x_3+b=0\\1*w_1x_1+0*w_2x_2+0*w_3x_3+b=0 \end{matrix}\right.\Rightarrow \left\{\begin{matrix} w_1x_1+w_2x_2+b=0\\w_1x_1+b=0 \end{matrix}\right. {1∗w1​x1​+1∗w2​x2​+0∗w3​x3​+b=01∗w1​x1​+0∗w2​x2​+0∗w3​x3​+b=0​⇒{w1​x1​+w2​x2​+b=0w1​x1​+b=0​即两个超平面共享了 w 1 w_1 w1​参数，同理可以推导出其他节点的参数共享情况。所以在多层感知机中，每一层的空间划分都存在大量的参数共享情况，这也是多层感知机的过参数化不容易过拟合的原因之一。

参数共享带来了很多好处，但是也同样带来了坏处，当层数加深时因为层内的参数共享这种约束的存在，使得模型变得更难训练。

总结

通过本篇文章，希望大家能理多层感知机分类模型的数学原理与编码逻辑，下一篇文章可能分析卷积网络或反向传播过程或者多层感知机的一些补充内容。代码已开源 DNNexp。

参考文献

1. On the Number of Linear Regions of Deep Neural Networks
2. On the number of response regions of deep feed forward networks with piece- wise linear activations
3. On the Expressive Power of Deep Neural Networks
4. On the Number of Linear Regions of Convolutional Neural Networks
5. Bounding and Counting Linear Regions of Deep Neural Networks
6. Multilayer Feedforward Networks Are Universal Approximators
7. Facing up to arrangements: face-count formulas for partitions of space by hyperplanes
8. An Introduction to Hyperplane Arrangements
9. Combinatorial Theory: Hyperplane Arrangements
10. Partern Recognition and Machine Learning
11. Scikit-Learn Decision Tree

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！