2023年华为杯研赛研究生数学建模D题！数模讲师与您一起探索建模过程。

我是数学建模讲师小L。我主要为大学生讲授数学建模的基本思路和解题技巧

在数学建模过程中,需要强调建模思维的培养。我会通过大量案例,讲解不同类型问题的建模思路,让学生掌握抽象问题、确定目标、建立模型、求解及验证解的一般步骤。

这次数学建模D题，我这里也做我的简单分析：

问题重述： 假设有一地区的碳排放量与经济（GDP）、人口、化石能源消费量和非化石能源消费量之间存在关联关系。我们希望通过多元线性回归模型来预测未来该地区的碳排放量，同时考虑这些因素的影响。为了解决这个问题，我们需要进行以下步骤：

问题一：区域碳排放量以及经济、人口、能源消费量的现状分析
建立合适的指标体系，描述该地区的经济、人口、化石能源消费量、非化石能源消费量以及碳排放量的状况，并考虑各部门（能源供应、工业、建筑、交通、居民生活、农林等）的碳排放情况。

分析该地区在过去几年中碳排放量的变化趋势，并确定哪些因素对碳排放量产生了影响。
研判该地区实现碳达峰和碳中和目标所面临的主要挑战，为双碳路径规划提供依据。

问题二：区域碳排放量以及经济、人口、能源消费量的预测模型
基于人口、经济（GDP）变化的模型，预测未来该地区碳排放量。
确定碳排放量与人口、GDP、化石能源消费量、非化石能源消费量之间的关联关系。
在多情景条件下，利用模型估计未来碳排放量，考虑到不同的假设，如经济增长、人口变化和能源结构的改变。

问题三：区域双碳（碳达峰与碳中和）目标与路径规划方法
设计不同情景，与碳达峰和碳中和的时间节点以及能效提升和非化石能源消费比重提升相关联。
制定区域碳达峰和碳中和的具体目标，包括GDP、人口、能源消费量的目标值，以及能效提升、产业升级、能源脱碳和电气化的定性与定量分析。

问题一：多元线性回归

数据收集

首先，需要收集历史数据，包括区域的碳排放量、GDP、人口数量、化石能源消费量、非化石能源消费量等指标。确保数据的时间范围涵盖了你要分析的十二五和十三五期间的数据。

建立多元线性回归模型

多元线性回归模型可以用来评估不同指标之间的关系。在这里，我们假设碳排放量是因变量（Y），而GDP、人口数量、化石能源消费量、非化石能源消费量是自变量（X1、X2、X3、X4）。回归模型如下：

$Y=\beta 0+\beta 1X1+\beta 2X2+\beta 3X3+\beta 4X4+\epsilon$

其中，Y 表示碳排放量，X1 表示 GDP，X2 表示人口数量，X3 表示化石能源消费量，X4 表示非化石能源消费量，β0 是截距，β1、β2、β3、β4 是各自变量的回归系数，ε 表示误差项。

估计回归系数

使用统计软件（例如Python中的Scikit-Learn或R语言）来估计回归系数。估计后的回归方程将提供每个自变量对碳排放的影响程度。你可以使用最小二乘法等技术来估计系数。

检验回归模型的拟合度

要评估模型的拟合度，可以使用各种统计指标，如决定系数（R-squared）、调整决定系数（Adjusted R-squared）、F统计量等。

决定系数（R-squared）表示模型中解释变量的方差所占比例，越接近1越好。
调整决定系数（Adjusted R-squared）考虑了模型中自变量的数量，以避免过度拟合。
F统计量用于检验模型是否显著，即自变量是否对因变量有显著影响。

解释回归系数

解释回归系数可以帮助你理解不同因素对碳排放的影响。系数的正负号表示变量的影响方向，系数的大小表示影响的强度。例如，如果某个自变量的系数为正且显著，说明该因素与碳排放正相关；如果系数为负且显著，说明负相关。

预测和评估

一旦建立了回归模型并估计了系数，你可以使用模型来进行未来的预测。通过输入未来的GDP、人口数量、能源消费量等数据，可以估计未来的碳排放量。同时，使用模型的误差项来评估模型的精度。

计算多元线性回归模型中的回归系数，通常使用最小二乘法或其他拟合方法。最小二乘法是一种常用的方法，用于最小化实际观测值与模型预测值之间的残差平方和。

假设你有一个多元线性回归模型如下：

$Y=\beta 0+\beta 1X1+\beta 2X2+...+\beta n\ast Xn+\epsilon$

其中，$Y$ 表示因变量，$X1、X2、...、Xn$ 表示自变量，$β0、β1、β2、…、βn $表示回归系数，$ε $表示误差项。

计算回归系数的步骤如下：

1. 准备数据：

收集并整理你的数据，包括因变量$ Y$ 和自变量 $X1、X2、...、Xn$。确保数据没有缺失值。
2. 计算均值：

对所有自变量 $X1、X2、...、Xn$以及因变量 $Y$计算均值。
3. 计算差异和协方差：

计算每对自变量之间的协方差（covariance）和每个自变量与因变量之间的协方差。协方差可以用以下公式表示：

c o v ( X i , X j ) = Σ [ ( X i − X ˉ i ) ∗ ( X j − X ˉ j ) ] / ( N − 1 ) cov(Xi, Xj) = Σ[(Xi - X̄i) * (Xj - X̄j)] / (N - 1) cov(Xi,Xj)=Σ[(Xi−Xˉi)∗(Xj−Xˉj)]/(N−1)

其中，Xi 和 Xj 分别是两个自变量的观测值，X̄i 和 X̄j 分别是两个自变量的均值，Y 是因变量的观测值，Ȳ 是因变量的均值，N 是样本大小。

4. 计算回归系数：

使用最小二乘法，计算回归系数 β0、β1、β2、…、βn 的估计值。回归系数的计算公式如下：

β 0 = Y ˉ − β 1 ∗ X ˉ 1 − β 2 ∗ X ˉ 2 − . . . − β n ∗ X ˉ n β0 = Ȳ - β1 * X̄1 - β2 * X̄2 - ... - βn * X̄n β0=Yˉ−β1∗Xˉ1−β2∗Xˉ2−...−βn∗Xˉn
$\beta 1=cov(X1,Y)/cov(X1,X1)$
$\beta 2=cov(X2,Y)/cov(X2,X2)$
…
$\beta n=cov(Xn,Y)/cov(Xn,Xn)$

这些公式给出了回归系数的估计值，其中 β0 是截距项，β1、β2、…、βn 是各自变量的回归系数。

5. 计算误差项（残差）：

使用估计的回归系数，计算每个观测值的残差，即实际观测值与模型预测值之间的差异： $\epsilon =Y-(\beta 0+\beta 1X1+\beta 2X2+...+\beta n\ast Xn)$

本讲师提供了两种代码，分别为python和matlab的实现，供大家进行学习：

import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score# 创建一个示例数据集
data = {'Carbon_Emissions': [120, 130, 140, 150, 160],  # 碳排放量'GDP': [5000, 5500, 6000, 6500, 7000],  # GDP'Population': [1000, 1100, 1200, 1300, 1400],  # 人口'Fossil_Fuel_Consumption': [400, 420, 440, 460, 480],  # 化石能源消费'Non_Fossil_Fuel_Consumption': [80, 90, 100, 110, 120]  # 非化石能源消费
}（实际的数据可以进到下方文档查看）# 创建DataFrame
df = pd.DataFrame(data)# 定义自变量和因变量
X = df[['GDP', 'Population', 'Fossil_Fuel_Consumption', 'Non_Fossil_Fuel_Consumption']]
y = df['Carbon_Emissions']# 创建线性回归模型
model = LinearRegression()# 拟合模型
model.fit(X, y)# 获取回归系数
intercept = model.intercept_
coefficients = model.coef_print("截距项 (Intercept):", intercept)
print("回归系数 (Coefficients):", coefficients)# 预测碳排放量
new_data = {'GDP': [7500],  # 替换为你要预测的新数据'Population': [1500],  # 替换为你要预测的新数据'Fossil_Fuel_Consumption': [500],  # 替换为你要预测的新数据'Non_Fossil_Fuel_Consumption': [130]  # 替换为你要预测的新数据
}new_df = pd.DataFrame(new_data)
predicted_emissions = model.predict(new_df)print("预测的碳排放量:", predicted_emissions)# 计算决定系数
y_pred = model.predict(X)
r_squared = r2_score(y, y_pred)print("决定系数 (R-squared):", r_squared)

matlab

% 创建示例数据集（请替换为你自己的数据）
Carbon_Emissions = [120, 130, 140, 150, 160];  % 碳排放量
GDP = [5000, 5500, 6000, 6500, 7000];  % GDP
Population = [1000, 1100, 1200, 1300, 1400];  % 人口
Fossil_Fuel_Consumption = [400, 420, 440, 460, 480];  % 化石能源消费
Non_Fossil_Fuel_Consumption = [80, 90, 100, 110, 120];  % 非化石能源消费
（实际的数据可以进到下方文档查看）
% 创建自变量矩阵X
X = [GDP', Population', Fossil_Fuel_Consumption', Non_Fossil_Fuel_Consumption'];% 创建因变量向量y
y = Carbon_Emissions';% 创建线性回归模型
mdl = fitlm(X, y, 'linear');% 获取回归系数
coefficients = mdl.Coefficients.Estimate;% 输出回归系数
disp('回归系数：');
disp(coefficients);% 预测碳排放量（假设有新的输入数据）
new_data = [7500, 1500, 500, 130];  % 替换为你要预测的新数据
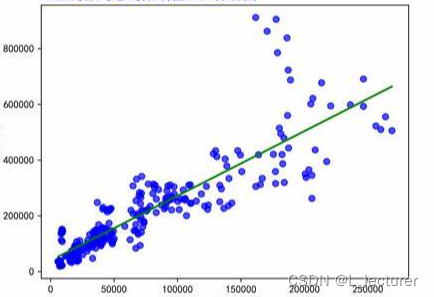
predicted_emissions = predict(mdl, new_data);fprintf('预测的碳排放量：%f\n', predicted_emissions);% 绘制散点图和回归线
figure;
scatter3(GDP, Population, Carbon_Emissions, 'filled');
xlabel('GDP');
ylabel('Population');
zlabel('Carbon Emissions');
title('Scatter Plot of Carbon Emissions vs. GDP and Population');hold on;% 创建一个网格以绘制回归平面
[xq, yq] = meshgrid(5000:100:7000, 1000:100:1400);
zq = coefficients(1) + coefficients(2) * xq + coefficients(3) * yq + coefficients(4) * 500 + coefficients(5) * 130;
mesh(xq, yq, zq, 'FaceAlpha', 0.5);hold off;

问题二：数据矩阵线性回归

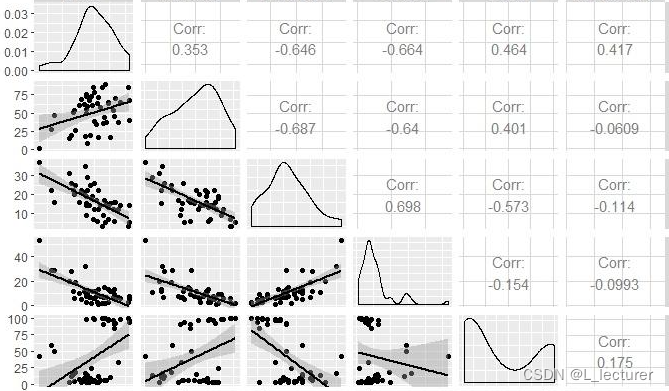
多元线性回归中，我们首先将数据表示为矩阵和向量。考虑到解决问题二，我们有以下表示：

数据矩阵 X：这是一个m×n 的矩阵，其中 m 表示观测样本的数量，n 表示自变量的数量。每行对应一个观测样本，每列对应一个自变量。例如，X 可以表示为：

X = [ 1 G D P 1 P o p u l a t i o n 1 F o s s i l 1 N o n F o s s i l 1 1 G D P 2 P o p u l a t i o n 2 F o s s i l 2 N o n F o s s i l 2 ⋮ ⋮ ⋮ ⋮ ⋮ 1 G D P m P o p u l a t i o n m F o s s i l m N o n F o s s i l m ] X = \begin{bmatrix} 1 & GDP_1 & Population_1 & Fossil_1 & NonFossil_1 \\ 1 & GDP_2 & Population_2 & Fossil_2 & NonFossil_2 \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 1 & GDP_m & Population_m & Fossil_m & NonFossil_m \\ \end{bmatrix} X= ​11⋮1​GDP1​GDP2​⋮GDPm​​Population1​Population2​⋮Populationm​​Fossil1​Fossil2​⋮Fossilm​​NonFossil1​NonFossil2​⋮NonFossilm​​ ​
这里，每一行代表一个观测样本，包括一个截距项（1）、GDP、人口、化石能源消费和非化石能源消费。

因变量向量 Y：这是一个 $m\times 1$ 的列向量，包含每个观测样本对应的碳排放量。例如，Y 可以表示为：

Y = [ C a r b o n 1 C a r b o n 2 ⋮ C a r b o n m ] Y = \begin{bmatrix} Carbon_1 \\ Carbon_2 \\ \vdots \\ Carbon_m \\ \end{bmatrix} Y= ​Carbon1​Carbon2​⋮Carbonm​​ ​

多元线性回归模型可以表示为矩阵形式如下：
$Y=X\beta +ϵ$
其中，

Y 是 $m\times 1$的因变量向量。
X 是 $m\times (n+1)$的数据矩阵，包括截距项和所有自变量。
$\beta$ 是 $(n+1)\times 1$的回归系数向量，包括截距项和各自变量的系数。
$ϵ$ 是 $m\times 1$ 的误差向量，包含了模型无法解释的随机误差。
为了估计回归系数 \betaβ，我们使用最小二乘法来最小化误差平方和：
min ⁡ β ∣ ∣ Y − X β ∣ ∣ 2 \min_{\beta} ||Y - X\beta||^2 minβ​∣∣Y−Xβ∣∣2
为了估计回归系数 $\beta$，我们可以使用最小二乘法最小化残差平方和 ϵ T ϵ \epsilon^T\epsilon ϵTϵ
,其中 $ϵ$ 是误差向量。通过对这个目标函数对 $\beta$ 求偏导数，并令导数等于零，可以获得最小二乘估计：

β ^ = ( X T X ) − 1 X T Y \hat{\beta} = (X^TX)^{-1}X^TY β^​=(XTX)−1XTY
其中， ( X T X ) − 1 (X^TX)^{-1} (XTX)−1表示 X T X X^TX XTX的逆矩阵。

回归系数 β ^ \hat{\beta} β^​ 反映了自变量与因变量之间的线性关系。每个 β ^ i \hat{\beta}_i β^​i​ 表示对应自变量 X i X X_iX Xi​X 对因变量的影响。正的系数表示自变量的增加与因变量的增加正相关，负的系数表示负相关。

python
import numpy as np
import pandas as pd
import statsmodels.api as sm# 创建示例数据集（请替换为你自己的数据）
data = {'Year': [2010, 2011, 2012, 2013, 2014],'Carbon_Emissions': [120, 130, 140, 150, 160],'GDP': [5000, 5500, 6000, 6500, 7000],'Population': [1000, 1100, 1200, 1300, 1400],'Fossil_Fuel_Consumption': [400, 420, 440, 460, 480],'Non_Fossil_Fuel_Consumption': [80, 90, 100, 110, 120]
}# 创建DataFrame
df = pd.DataFrame(data)# 定义自变量和因变量
X = df[['GDP', 'Population', 'Fossil_Fuel_Consumption', 'Non_Fossil_Fuel_Consumption']]
Y = df['Carbon_Emissions']# 添加截距项
X = sm.add_constant(X)# 建立多元线性回归模型
model = sm.OLS(Y, X).fit()# 输出回归结果摘要
print(model.summary())# 预测碳排放量（假设有新的输入数据）
new_data = pd.DataFrame({'GDP': [7500],'Population': [1500],'Fossil_Fuel_Consumption': [500],'Non_Fossil_Fuel_Consumption': [130]
})# 添加截距项
new_data = sm.add_constant(new_data)# 进行预测
predicted_emissions = model.predict(new_data)print('预测的碳排放量：', predicted_emissions)

matlab

% 创建示例数据集（请替换为你自己的数据）
Year = [2010, 2011, 2012, 2013, 2014];
Carbon_Emissions = [120, 130, 140, 150, 160];
GDP = [5000, 5500, 6000, 6500, 7000];
Population = [1000, 1100, 1200, 1300, 1400];
Fossil_Fuel_Consumption = [400, 420, 440, 460, 480];
Non_Fossil_Fuel_Consumption = [80, 90, 100, 110, 120];% 创建数据矩阵 X 和因变量向量 Y
X = [GDP', Population', Fossil_Fuel_Consumption', Non_Fossil_Fuel_Consumption'];
Y = Carbon_Emissions';% 添加截距项
X = [ones(size(X, 1), 1), X];% 建立多元线性回归模型
mdl = fitlm(X, Y);% 输出回归结果摘要
disp(mdl);% 预测碳排放量（假设有新的输入数据）
new_data = [7500, 1500, 500, 130];
new_data = [1, new_data]; % 添加截距项
predicted_emissions = predict(mdl, new_data);disp(['预测的碳排放量：', num2str(predicted_emissions)]);

具体余下内容请与我在以下观看与讨论
2023年华为杯研赛研究生数学建模D题！，小L数模讲师与您一起探索建模过程。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！