追根溯源——回溯算法
最近几天在leetcode上刷到排列组合这一类的问题多了起来.
.基本的解决思路就是“回溯算法”,乍一看感觉非常高大上,其实也就是披着多叉树遍历外套的暴力破解法,做多了就会发现这就像循环遍历数组一样,套路固定,故准备总结在此,以供交流探讨。
2020年9月15日10:04:30
第4次更次博客,今天的leetcode题目是解数独,用回溯法解的非常漂亮,忍不住想分享出来。
2020年9月18日09:42:44
第5次更新,今天的leetcode题目虽然是求排列组合的全排列,但是涉及到去重,还有一个涉及到去重的问题是组合总和II,基本思路都是先进行排序,然后再做一系列操作。
1 模板
举个例子:输出一串数字[1,2,3]的全排列[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]。
这个问题交给人类来解决的话肯定是先固定第一位为 1,然后第二位可以是 2,那么第三位只能是 3;然后可以把第二位变成 3,第三位就只能是 2 了;然后就只能变化第一位,变成 2,然后再穷举后两位,以此类推......
就像下面这样的一个树形结构:
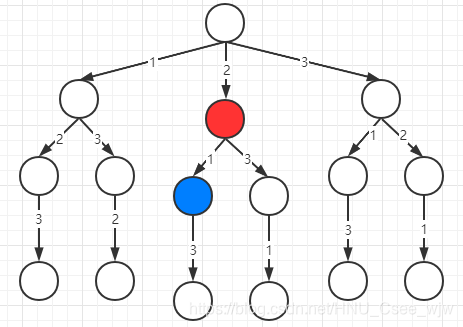
当我们停留在每一个 节点上时,都需要做一个决策,例如停留在图中红色节点上时,有[1, 3]两个数字可以做选择,如果选择了1之后再选择数字3(最后一个数字只有一个选项),则已经找到了一个不重复的数字,这一次的选择就结束了,我们会退回红色的节点继续向右子树搜索,以此类推......直到找到左右的结果。
这其实就是回溯算法,中学的时候就已经不自觉地掌握了。我们可以抽象一点,把整个算法的解决模板给概括出来,即:
解决一个回溯问题,实际上就是一个决策树的遍历过程,确定了以下三个条件,问题就迎刃而解了:
- 路径:已经做出的选择
- 选择列表:当前可以做的选择
- 结束条件(递归出口):到达决策的底层,没有选择可做的条件
伪代码如下:
List result = new ArrayList<>();
private void backtrack(路径, 选择列表){if(满足结束条件){result.add(路径);return;}for(选择 : 选择列表){做选择;backtrack(路径, 选择列表);撤销选择;}} 上面蓝色文字“决策”对应的就是代码中的“做选择”,“结束”对应“满足结束条件”,“退回”对应“撤销选择”
其核心就是 for 循环里面的递归,在递归调用之前「做选择」,在递归调用之后「撤销选择」,特别简单。
多说无益,上例子。
2 排列组合问题
2.1 leetcode 77 组合

评论区里面的图画的已经非常直观了,我这里直接引用一下
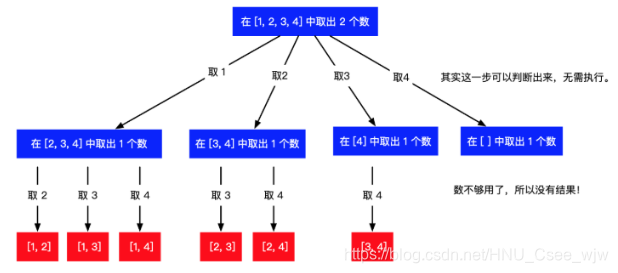
根据我上面给的三个条件,将其对应在本题中如下:
- 路径:就是图中红色方块部分,当然树干上面“取X”也是路径
- 选择列表:就是图中蓝色方块部分
- 结束条件:路径中包含k个数字时。
我们定义的函数其实就像是一个指针,将这棵树的所有节点都走一遍之后整个程序就执行完毕了,所得的结果就是正确结果。如何将这棵树所有的节点都走一遍?其实就是前序遍历,中序遍历,后序遍历:
private traverse(TreeNode root){for(TreeNode child : root.children){traverse(child);}}我们做选择以及撤销选择的动作正是在前序和后序的时间点做出的,即做了一个选择之后到下一个节点,将做的选择撤销以后回到上一个节点!
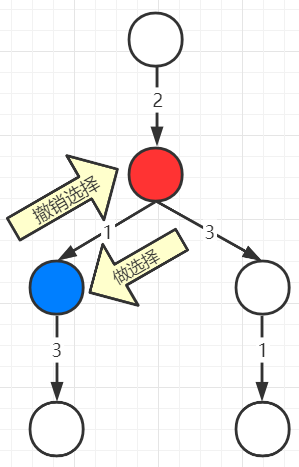
所以回溯算法的核心框架:
for(选择 : 选择列表){// 做选择将被选的项从候选表中删除;路径.add(选择);backtrack(路径, 选择列表);// 撤销选择路径.remove(选择);重新将被选的项加入候选表;}我们只要在递归之前做出选择,在递归之后撤销刚才的选择,就能正确得到每个节点的选择列表和路径。
本题解决方案如下:
class Solution {private List> result = new ArrayList<>();// 用一个栈来记录每一个组合private void findCombinations(int n, int k, int begin, Stack pre){if(pre.size() == k){result.add(new ArrayList<>(pre));return;}for(int i = begin; i <= n; i ++){pre.push(i);findCombinations(n, k, i + 1, pre); // 从下一个数字开始取// 当前数字的情况已经全部取完,弹出栈顶元素pre.pop();}}public List> combine(int n, int k) {if (n <= 0 || k <= 0 || n < k) {return result;}findCombinations(n, k, 1, new Stack<>());return result;}
} 这一部分就是递归出口(可以结合题意理解,我们只要找到k个数字就好)

每一个数字 i 就是要做的选择

返回用一个List来存储(当然其他的数据结构都可以~)
![]()
撤销选择操作,其实就是做选择的逆动作
![]()
2.2 leetcode 216 组合总和III
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。
示例 1:
输入: k = 3, n = 7
输出: [[1,2,4]]
这种找出总和为某数字的问题,套路也很固定,只需在回溯函数里多添加一个遍历target用于记录求和的目标是多少即可。
class Solution {private List> result = new ArrayList<>();private List temp = new ArrayList<>();public List> combinationSum3(int k, int n) {dfs(k, n, 1);return result;}private void dfs(int k, int sum, int start){if(k == 0 && sum == 0){ // 符合条件result.add(new ArrayList<>(temp)); // 注意深拷贝和浅拷贝!!必须是new一个新数组return;}if(k == 0 || sum < 0) return; // 不符合条件for(int i = start; i <= 9; i ++){temp.add(i);dfs(k - 1, sum - i, i + 1);temp.remove(temp.size() - 1); // 回溯}return;}} 2.3 leetcode 60 组合总和III
给出集合 [1,2,3,…,n],其所有元素共有 n! 种排列。
按大小顺序列出所有排列情况,并一一标记,当 n = 3 时, 所有排列如下:
"123"
"132"
"213"
"231"
"312"
"321"
给定 n 和 k,返回第 k 个排列。

leetcode上面的一个题解很优秀,这里引用一下。
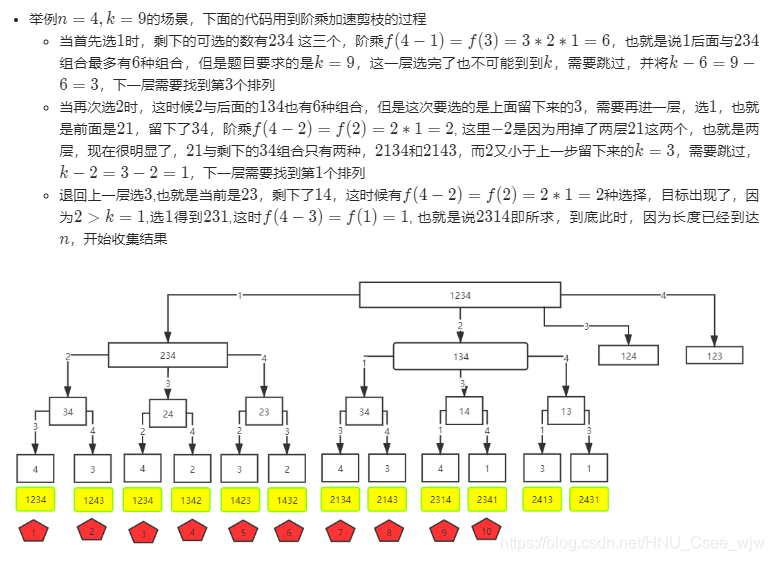
public String getPermutation(int n, int k) {int[] nums = new int[n];//生成nums数组for (int i = 0; i < n; i++){nums[i] = i + 1;} boolean[] used = new boolean[n];//记录当前的索引的数是否被使用过return dfs(nums, new ArrayList(), used, 0, n, k);}/*** @param nums 源数组* @param levelList 每一层的选择* @param used 数组的元素是否被使用过* @param depth 深度,也就是当前使用的元素的索引* @param n 上限值* @param k 第k个* @return 第k个排列*/private String dfs(int[] nums, List levelList, boolean[] used, int depth, int n, int k) {if (depth == n) {//触发出口条件,开始收集结果集StringBuilder res = new StringBuilder();for (String s : levelList){res.append(s);}return res.toString();}int cur = factorial(n - depth - 1);//当前的depth也就是索引,有多少排列数for (int i = 0; i < n; i++) {if (used[i]) continue;//当前元素被使用过,做剪枝if (cur < k) {//当前的排列组合数小于k,说明就算这一层排完了,也到不了第k个,剪枝k -= cur;continue;}levelList.add(nums[i] + "");//list收的是string类型used[i] = true;//当前元素被使用过标记return dfs(nums, levelList, used, depth + 1, n, k);}return null;}//返回n的阶乘,如3!=3*2*1=6private int factorial(int n) {int res = 1;while (n > 0) {res *= n--;}return res;} 2.4 全排列II
给定一个可包含重复数字的序列,返回所有不重复的全排列。

涉及到去重的问题,一般思路都是将候选数组进行排序,然后再做一系列操作。这里我们选择对原数组排序,保证相同的数字都相邻,然后每次填入的数一定是这个数所在重复数集合中「从左往右第一个未被填过的数字」,即如下的判断条件:
if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {continue;
}详细代码如下:
class Solution {private boolean[] used;private List> result;public List> permuteUnique(int[] nums) {used = new boolean[nums.length];result = new ArrayList<>();Arrays.sort(nums);backtrack(nums, new ArrayList<>(), 0);return result;}private void backtrack(int[] nums, List path, int index){if(index >= nums.length){result.add(new ArrayList(path));return;}for(int i = 0; i < nums.length; i ++){if(used[i]){continue;}// 只使用重复数字的第一个// !used[i - 1] 说明当前重复数字左边还有未使用过的if(i > 0 && nums[i] == nums[i - 1] && !used[i - 1]){continue;}path.add(nums[i]);used[i] = true;backtrack(nums, path, index + 1);// 回溯used[i] = false;path.remove(path.size() - 1);}}
}
3 子序列问题
当然排列组合问题当然不仅限于全排列问题,还有可能让我们从候选项中选出一些元素出来,就是所谓的求子序列。
leetcode 1079 活字印刷
你有一套活字字模 tiles,其中每个字模上都刻有一个字母 tiles[i]。返回你可以印出的非空字母序列的数目。
注意:本题中,每个活字字模只能使用一次。
示例 1:
输入:"AAB"
输出:8
解释:可能的序列为 "A", "B", "AA", "AB", "BA", "AAB", "ABA", "BAA"。
同样是明确三个条件:
- 路径:同上题,先前已经选择的字母组成的字符串。
- 选择列表:剩下可供选择的字母,即 title 中除了被用掉的字母之外的所有字母
- 结束条件:由于每一个结果的长度不是固定的,而且我们只需要统计个数,所以在生成"AA"的途中我们必然会经过"A",这是计数器也要进行累加。
这个题目算是比较特殊的,只用统计最后子序列的个数,所以在递归调用时不需要再传入路径和选择列表,不过在分析问题的时候还是要明确这两个概念,这样才不至于代码出错。
参考代码:
class Solution {int result = 0;public int numTilePossibilities(String tiles) {char[] counter = new char[26];for(int i = 0; i < tiles.length(); i ++){counter[tiles.charAt(i) - 'A'] ++;}backtrack(counter);return result;}private void backtrack(char[] counter){for(int i = 0; i < 26; i ++){// 剪枝,即排除无效选择if(counter[i] == 0) continue;// 进行一次具体选择,本题就是 i 计数器减 1counter[i] --;// 一次有效枚举,总的计数器加 1result ++;// 继续回溯:递归 + 选择(尽可能剪枝) + 回退之前的现场恢复backtrack(counter);// 回退之前,也就是进入另一分支之前,恢复当前分支的改动counter[i] ++;}}
}由于并不需要输出最后得结果,所以只用将每个字母出现的频率统计出来就好(所幸英文字母的数量是可数的)。

一个选择就是选了一个字母,相应的频率减一就ok。
![]()
撤销选择就是将刚刚选择的字母重新放回候选列表中,即相应的字母频率加一。
![]()
4 子序列问题2
上面的问题其实是讨巧的,英文单词个数只有26个,并且只用输出序列的个数就可以了。如果将字母换做数字,那么就还是要老老实实地按照回溯的流程去做。
leetcode 面试题 08.04 幂集
幂集。编写一种方法,返回某集合的所有子集。集合中不包含重复的元素。
说明:解集不能包含重复的子集。
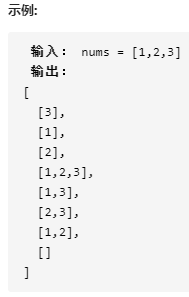
分析的三个条件和上题类似,只不过是将字母变作数字。
由于是子序列,所以我们在从 0 到 length - 1 遍历候选数组时有一些数字是可以不选的,因此就会在递归调用时产生分叉,只需多考虑一种情况即可。
class Solution {List> result = new ArrayList<>();List temp = new ArrayList<>();public List> subsets(int[] nums) {dfs(nums, 0);return result;}private void dfs(int[] nums, int index){if(index >= nums.length){result.add(new ArrayList<>(temp)); // 注意浅拷贝return;}// 不选择当前数字dfs(nums, index + 1);// 选择当前数字temp.add(nums[index]);dfs(nums, index + 1);// 回溯temp.remove(temp.size() - 1);}
} 当遍历数组的索引值超出数组范围时就是返回条件:
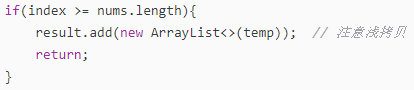
有两种情况需要考虑:选择当前数字 / 不选当前数字 :
如果选择了当前数字的话就需要在结果集temp中进行添加

撤销选择操作就是将刚刚选择的数字从路径中删除即可:
![]()
5 24点游戏
leetcode 679 24点游戏
一共有 4 个数和 3 个运算操作,因此可能性非常有限。一共有多少种可能性呢?
首先从 4 个数字中有序地选出 2 个数字,共有 4×3=12 种选法,并选择加、减、乘、除 4 种运算操作之一,用得到的结果取代选出的 2 个数字,剩下 3 个数字。
实现时,有一些细节需要注意。
- 除法运算为实数除法,因此结果为浮点数,列表中存储的数字也都是浮点数。在判断结果是否等于 24 时应考虑精度误差,这道题中,误差小于 10^{-6}可以认为是相等。
- 进行除法运算时,除数不能为 0,如果遇到除数为 0 的情况,则这种可能性可以直接排除。由于列表中存储的数字是浮点数,因此判断除数是否为 0 时应考虑精度误差,这道题中,当一个数字的绝对值小于 10^{-6}时,可以认为该数字等于 0。

一共有 4 个数和 3 个运算操作,因此可能性非常有限。
首先从 4 个数字中有序地选出 2 个数字,共有 4×3=12 种选法,并选择加、减、乘、除 4 种运算操作之一,用得到的结果取代选出的 2 个数字,剩下 3 个数字。
实现时,有一些细节需要注意。
- 除法运算为实数除法,因此结果为浮点数,列表中存储的数字也都是浮点数。在判断结果是否等于 24 时应考虑精度误差,这道题中,误差小于 10^{-6}可以认为是相等。
- 进行除法运算时,除数不能为 0,如果遇到除数为 0 的情况,则这种可能性可以直接排除。由于列表中存储的数字是浮点数,因此判断除数是否为 0 时应考虑精度误差,这道题中,当一个数字的绝对值小于 10^{-6}时,可以认为该数字等于 0。
class Solution {static final int ADD = 0, MULTIPLY = 1, SUBTRACT = 2, DIVIDE = 3;public boolean judgePoint24(int[] nums) {List list = new ArrayList();for (int num : nums) {list.add((double) num);}return backtrack(list);}public boolean backtrack(List list) {if (list.size() == 0) {return false;}if (list.size() == 1) { return Math.abs(list.get(0) - 24) < 1e-6;}int size = list.size();for (int i = 0; i < size; i++) {for (int j = 0; j < size; j++) {if (i != j) { // 选出来i,j这两个位置的数字做四则运算List list2 = new ArrayList();for (int k = 0; k < size; k++) {if (k != i && k != j) { // 剩下的数字保持不变list2.add(list.get(k));}}for (int k = 0; k < 4; k++) {if (k == ADD) { // 加法list2.add(list.get(i) + list.get(j));} else if (k == MULTIPLY) { // 乘法list2.add(list.get(i) * list.get(j));} else if (k == SUBTRACT) { // 减法list2.add(list.get(i) - list.get(j));} else if (k == DIVIDE) { // 除法if (Math.abs(list.get(j)) < 1e-6) { // 分母不能为0continue;} else {list2.add(list.get(i) / list.get(j));}}if (backtrack(list2)) {return true;}// 回溯list2.remove(list2.size() - 1);}}}}return false;}
} 6 N皇后问题(放置问题)
决策树的每一层表示棋盘的每一行,每个节点可以做的选择是在该行任意位置放置一个皇后。
路径:board,其中小于row的那些行都已经选好了放皇后的位置
选择列表:第row行的每一个位置
返回条件:row超出borad范围
class Solution {private List> res = new ArrayList<>();public List> solveNQueens(int n) {List board = new ArrayList<>();for(int i = 0; i < n; i ++){String temp = "";for(int j = 0; j < n ; j ++){temp += '.';}board.add(temp);}backtrack(board, 0);return res;}// 路径:board,其中小于row的那些行都已经选好了放皇后的位置// 选择列表:第row行的每一个位置// 返回条件:row超出borad范围private void backtrack(List board, int row){if(row == board.size()){res.add(new ArrayList<>(board));return;}int n = board.get(row).length();for(int col = 0; col < n; col ++){if(!valid(board, row, col)){continue;}char[] str = board.get(row).toCharArray();// 做选择 str[col] = 'Q';board.set(row, new String(str));// 回溯backtrack(board, row + 1);// 撤销选择str[col] = '.';board.set(row, new String(str));}}// 是否可以在该位置放置private boolean valid(List board, int row, int col){int n = board.get(row).length();// 检查列for(int i = 0; i < n; i ++){if(board.get(i).charAt(col) == 'Q'){return false;}}// 检查右上方for(int i = row - 1, j = col + 1; i >= 0 && j < n; i --, j ++){if(board.get(i).charAt(j) == 'Q'){return false;}}// 检查左上方for(int i = row - 1, j = col - 1; i >=0 && j >= 0; i --, j --){if(board.get(i).charAt(j) == 'Q'){return false;}}return true;}
} 7 搜索所有可行解
7.1 leetcode 39 组合总和
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
所有数字(包括 target)都是正整数。
解集不能包含重复的组合。

定义递归函数 backtrack(int[] candidates, int target, List
递归的终止条件为 target <= 0 或者 candidates 数组被全部用完。那么在当前的函数中,每次我们可以选择跳过不用第 startIndex 个数,即执行 backtrack(candidates, target, path, startIndex + 1)。也可以选择使用第 startIndex个数,即执行 dfs(candidates, target - candidates[startIndex ], combine, startIndex ).
注意到每个数字可以被无限制重复选取,因此搜索的下标仍为 startIndex 。
class Solution {List> result = new ArrayList<>();public List> combinationSum(int[] candidates, int target) {List path = new ArrayList<>();backtrack(candidates, target, path, 0);return result;}private void backtrack(int[] candidates, int target, List path, int startIndex){if(startIndex == candidates.length){return;}if(target == 0){result.add(new ArrayList(path));return;}// 不选当前数字backtrack(candidates, target, path, startIndex + 1);// 选当前数字if(target >= candidates[startIndex]){path.add(candidates[startIndex]);// 每个数字可以被无限制重复选取,因此搜索的下标仍为 startIndexbacktrack(candidates, target - candidates[startIndex], path, startIndex);// 回溯path.remove(path.size() - 1);}}
} 7.2 组合总和II
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次。
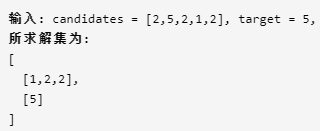
和上面的题目框架是类似的,只不过上题要求数字可以无限次使用,本题要求数字只能被用一次,所以需要去重操作,一个简单的去重思路是将数组进行从小到大排序,当后面一个数字等于前面一个数字时直接continue。其余框架不变。
class Solution {List> result = new ArrayList<>();public List> combinationSum2(int[] candidates, int target) {List path = new ArrayList<>();Arrays.sort(candidates);backtrack(candidates, target, path, 0); return result;}private void backtrack(int[] candidates, int target, List path, int startIndex){if(target == 0){result.add(new ArrayList(path));return;}for(int i = startIndex; i < candidates.length; i ++){if(candidates[i] > target){break;}// 保证不重复if(i > startIndex && candidates[i] == candidates[i-1]){continue;}path.add(candidates[i]);backtrack(candidates, target - candidates[i], path, i + 1);path.remove(path.size() - 1);}}
} 8 回溯和图的遍历结合
leetcode 79 单次搜索
给定一个二维网格和一个单词,找出该单词是否存在于网格中。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

设函数check(i,j,k) 判断以网格的 (i, j) 位置出发,能否搜索到单词 word[k..]
路径:当前匹配到的位置k
返回条件:k移动到word尾或者i,j超出二维数组边界
class Solution {public boolean exist(char[][] board, String word) {for (int i = 0; i < board.length; ++i) {for (int j = 0; j < board[i].length; ++j) {if (board[i][j] == word.charAt(0)) {if (backtrack(board, word, i, j, 0)) return true;}}}return false;}private boolean backtrack(char[][] board, String word, int i, int j, int k){if (k == word.length()) {return true;}if (i < 0 || j < 0 || i >= board.length || j >= board[i].length) {return false;}if (word.charAt(k) != board[i][j]) {return false;}// 匹配当前位置char t = board[i][j];board[i][j] = '0';boolean res = backtrack(board, word, i + 1, j, k + 1) || backtrack(board, word, i - 1, j, k + 1) || backtrack(board, word, i, j + 1, k + 1) || backtrack(board, word, i, j - 1, k + 1);// 回溯board[i][j] = t;return res;}
}
9 求解数独
求解数独的思路就是对每一个格子所有可能的数字1-9进行穷举,基于此,我们可以写出代码框架:
public void solveSudoku(char[][] board) {backtrack(board, 0, 0);
}// 从左上角(r,c)开始回溯求解数组
public void backtrack(char[][] board, int r, int c){int m = 9;int n = 9;// 对棋盘的每个位置进行穷举for (int i = r; i < m; i++) {for (int j = c; j < n; j++) {for (char ch = '1'; ch <= '9'; ch ++) {// 做选择board[i][j] = ch;// 继续穷举下一个backtrack(board, i, j + 1);// 撤销选择board[i][j] = '.';}}}
}如果 j 到最后一列了我们应该从下一行开始继续,如果 i 到最后一行了我们就等于穷举完了所有情况,返回即可。为了减少复杂度,我们可以让backtrack函数返回值为boolean,如果找到一个可行解就返回 true,这样就可以阻止后续的递归。
class Solution {public void solveSudoku(char[][] board) {backtrack(board, 0, 0);}// 从左上角(r,c)开始回溯求解数组public boolean backtrack(char[][] board, int r, int c){int m = 9;int n = 9;if(c == n){// 到最后一列则从下一行开始return backtrack(board, r + 1, 0);}if(r == m){return true;}// 对每个位置穷举for(int i = r; i < m; i ++){for(int j = c; j < n; j ++){// 此处已经有数字if(board[i][j] != '.'){return backtrack(board, i , j + 1);}for(char ch = '1'; ch <= '9'; ch ++){if(!isValid(board, i, j, ch)){continue;}board[i][j] = ch;if(backtrack(board, i, j + 1)){return true;}board[i][j] = '.';}// 穷举完仍没找到return false;}}return false;}public boolean isValid(char[][] board, int r, int c, char ch){for(int i = 0; i < 9; i ++){// 判断行是否有重复数字if(board[r][i] == ch){return false;}// 判断列是否有重复数字if(board[i][c] == ch){return false;}// 判断3×3区域内是否有重复数字if(board[(r/3)*3 + i/3][(c/3)*3 + i%3] == ch){return false;}}return true;}
}
10 总结
回溯算法就是个多叉树的遍历问题,关键就是在前序遍历和后序遍历的位置做一些操作。
写回溯函数时,需要维护走过的路径和当前可以做的选择列表,当满足结束条件时,将路径记入结果集。
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!