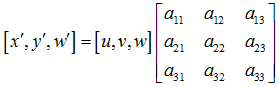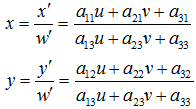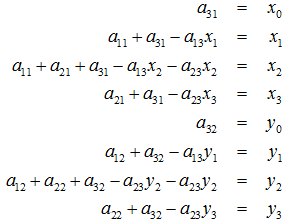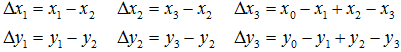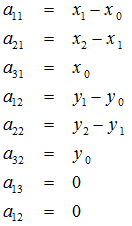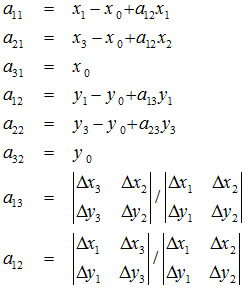转载：【图像处理】透视变换 （Perspective Transformation）原理介绍

透视变换(Perspective Transformation)是将图片投影到一个新的视平面(Viewing Plane)，也称作投影映射(Projective Mapping)。通用的变换公式为：

u,v是原始图片左边，对应得到变换后的图片坐标x,y,其中。

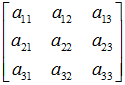
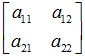
变换矩阵可以拆成4部分，表示线性变换，比如scaling，shearing和ratotion。用于平移，产生透视变换。所以可以理解成仿射等是透视变换的特殊形式。经过透视变换之后的图片通常不是平行四边形（除非映射视平面和原来平面平行的情况）。

重写之前的变换公式可以得到：

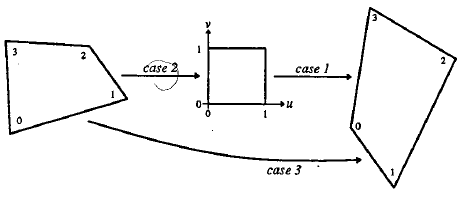
所以，已知变换对应的几个点就可以求取变换公式。反之，特定的变换公式也能新的变换后的图片。简单的看一个正方形到四边形的变换：变换的4组对应点可以表示成：

根据变换公式得到：

定义几个辅助变量：

都为0时变换平面与原来是平行的，可以得到：

不为0时，得到：

求解出的变换矩阵就可以将一个正方形变换到四边形。反之，四边形变换到正方形也是一样的。于是，我们通过两次变换：四边形变换到正方形+正方形变换到四边形就可以将任意一个四边形变换到另一个四边形。

————————————————

版权声明：本文为CSDN博主「xiaowei_cqu」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。

原文链接：https://blog.csdn.net/xiaowei_cqu/article/details/26471527

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！