洛谷 P1629 邮递员送信(dijkstra算法）

提示：如果你进来是为了学习dikstra算法的，抱歉你走错片场了

           这是一个小白的解题心路分享

题目描述

有一个邮递员要送东西，邮局在节点 11。他总共要送 n-1n−1 样东西，其目的地分别是节点 22 到节点 nn。由于这个城市的交通比较繁忙，因此所有的道路都是单行的，共有 mm 条道路。这个邮递员每次只能带一样东西，并且运送每件物品过后必须返回邮局。求送完这 n-1n−1 样东西并且最终回到邮局最少需要的时间。

输入格式

第一行包括两个整数，nn 和 mm，表示城市的节点数量和道路数量。

第二行到第 (m+1)(m+1) 行，每行三个整数，u,v,wu,v,w，表示从 uu 到 vv 有一条通过时间为

ww 的道路。

输出格式

输出仅一行，包含一个整数，为最少需要的时间。

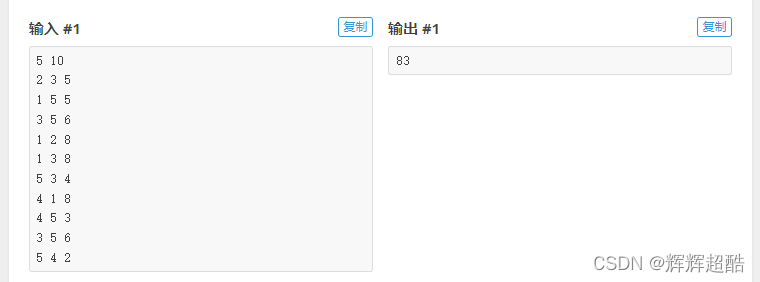
输入输出样例

解题历程：

刚刚看到这题时，先用了Floyd算法，也就是基于动态规划用dis[u][v]表示城市u到城市v的最短时间，代码如下：

#include
#include
#define endl "\n"
using namespace std;
typedef long long ll;
constexpr int maxn = 1005;
constexpr ll inf = 0x3f3f3f3f3f3f3f3fL;
ll dis[maxn][maxn];
int main(){memset(dis,0x3f,sizeof(dis));int n,m,t;cin >> n >> m;for(int i = 1;i<=n;i++)dis[i][i] = 0;//自己到自己的距离为0for(int i = 1;i<=m;i++){int u,v;ll w;cin >> u >> v >> w;dis[u][v] = w;}for(int k = 1;k<=n;k++)for(int i = 1;i<=n;i++)for(int j = 1;j<=n;j++)dis[i][j] = min(dis[i][j],dis[i][k]+dis[k][j]);ll ans = 0;for(int i = 2;i<=n;i++)ans += dis[1][i] + dis[i][1];cout << ans << endl;return 0;
}

 但是没注意时间复杂度，没过qwq

T了能理解，咱就是说为什么前四个点会WA呢？

然后猜测输入会有重边，把dis[u][v] = w 改成 dis[u][v] = min(dis[u][v]，w)交了一遍：

 果然输入卡重边（这里含泪建议各位写Floyd的时候要不要贪小便宜qwq）

当然对于这个题目来说，这个算法很明显不行，这时就得换算法了

由于最近刚刚学了dijktra,于是打算牵出来遛一遛（bushi

起点为1，终点为2->n,跑一遍就行，然后把所有的值加起来

但是起点为2->n,终点为1时怎么办呢？那就跑n-1遍dijkstra呗（小白思路，各位大佬轻点骂qwq

然后代码如下：

#include
#include
#include
#include
#define endl "\n"
using namespace std;
typedef long long ll;
constexpr int maxn = 2550;
constexpr ll inf = 0x3f3f3f3f3f3f3f3fL;struct edge{int v;ll w;bool operator<(const edge& a)const{return w>a.w;}//定义排序方式
}e;
vector  mp[maxn];
int dis[maxn];
void dij(int u){bool vis[maxn] = { false };//区别S点集和T点集，当vis[u] = true认为u在S点集中memset(dis,0x3f,sizeof(dis));//初始化disdis[u] = 0;priority_queue T;//这里并不是存边，这里存的时当前状态下某一点和他的dis，偷懒下T.push({u,0});//源点及其距离推入队列while(!T.empty()){u = T.top().v;//取出队列中当前dis最小的值T.pop();if(vis[u])//如果已经访问过就跳过continue;vis[u] = true;//将其加入S集// for(auto&[v,w]:mp[u]){int len = mp[u].size();//松弛其所有出边，并将其终点加入队列for(int i = 0;idis[u]+w){dis[v] = dis[u] + w;T.push({v,dis[v]});}}}
}int main(){int m,n,s,t;cin >> n >> m;for(int i = 0;i> u >> v >> w;e.v = v;e.w = w;mp[u].emplace_back(e);// e.v = u;// mp[v].emplace_back(e);}ll ans = 0;dij(1);for(int i = 2;i<=n;i++)ans += dis[i];for(int i = 2;i<=n;i++){dij(i);ans += dis[1];}cout << ans << endl;return 0;
}

然后又成功的T了

 然后突然我脑袋里冒出了一个大胆的想法：反向dijkstra建图！

既然正向的可以解决1到2->n的时间，反向的话是不是就能解决2->n到1了

然后相当于只用跑2遍dijkstra就行，有思路就好搞了对吧

AC代码如下：

#include
#include
#include
#include
#define endl "\n"
using namespace std;
typedef long long ll;
constexpr int maxn = 1005;
constexpr ll inf = 0x3f3f3f3f3f3f3f3fL;
struct edge{int v;ll w;bool operator<(const edge& a)const{return w>a.w;}//定义排序方式
}e;
struct edge2{int u;ll w;bool operator<(const edge& a)const{return w>a.w;}
}e2;//但是后来想了下好像这里没必要再定义个结构体，读者有兴趣可以试试减少代码量
vector  mp[maxn];
vector  mp2[maxn];
int dis[maxn] = { 0 };
void dij(int u){bool vis[maxn] = { false };//区别S点集和T点集，当vis[u] = true认为u在S点集中memset(dis,0x3f,sizeof(dis));//初始化disdis[u] = 0;priority_queue T;//这里并不是存边，这里存的时当前状态下某一点和他的disT.push({u,0});//源点及其距离推入队列while(!T.empty()){u = T.top().v;//取出队列中当前dis最小的值T.pop();if(vis[u])//如果已经访问过就跳过continue;vis[u] = true;//将其加入S集// for(auto&[v,w]:mp[u]){int len = mp[u].size();//松弛其所有出边，并将其终点加入队列for(int i = 0;idis[u]+w){dis[v] = dis[u] + w;T.push({v,dis[v]});}}}
}
void dij2(int v){bool vis[maxn] = { false };//咱就是说复制下上面的就行了对吧,u,v互换下memset(dis,0x3f,sizeof(dis));dis[v] = 0;priority_queue T;T.push({v,0});while(!T.empty()){v = T.top().v;T.pop();if(vis[v])continue;vis[v] = true;int len = mp2[v].size();for(int i = 0;idis[v]+w){dis[u] = dis[v] + w;T.push({u,dis[u]});}}}
}
int main(){int m,n,s,t;cin >> n >> m;for(int i = 0;i> u >> v >> w;e.v = v;e2.u = u;e.w = w;e2.w = w;mp[u].emplace_back(e);mp2[v].emplace_back(e2);}ll ans = 0;dij(1);for(int i = 2;i<=n;i++)ans += dis[i];dij2(1);for(int i = 2;i<=n;i++){ans += dis[i];}cout << ans << endl;return 0;
}

可能看着臭长了些，但能AC的代码都是好代码对吧【doge

好耶！！！

说明，写本文前搜了下发现已经有很多人用这个思路过了，但想了下我还是写了出来

因为不管怎么说这也是我这个小菜狗独立完成的不是【doge

好激动，就当是一次分享心情吧 ，各位看官笑笑就行，不用赞之类的

希望以后每次解决题目也会像今天这般欣喜

好了废话不多说，如有不对之处还请各位雅正（轻点骂，我怕疼bushi

祝各位天天AC好心情

!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

时隔不知多少天，我又写到这个题了，真是挺不错的

把刚写的新代码贴上去吧，思路没怎么变，还是反向建图

只是不像以前那么笨笨的写了两个函数了，少了很多行，但时间倒是慢了一些

应该是函数传入参数时将原来的那个拷贝过来导致的，但问题不大！

看着比较舒服（周围的花活就自动忽略把）

#include
#define endl "\n" 
#define AC return 0;
#define int long long
#define lowbit(i) ((i)&(-i))
#define YES {cout << "YES" << endl;}
#define NO  {cout << "NO"  << endl;}
#define IOS ios::sync_with_stdio(false);cin.tie(0);
#define pq priority_queue
#define rs pos << 1 | 1
#define ls pos << 1
using namespace std;
typedef double db;
typedef long long ll;
typedef vector VI;
typedef pair PII;
typedef vectorVII;
const int inf = 1e17+1e9+1;
const int MOD = 1e9+7;
const int N = 1e6+5;
//！！！！！！！！注意不能存在负边权！！！！！！！！！
struct edge{    int to;     //指向的节点int val;    //边权bool operator<(const edge &mm)const{return val > mm.val;}//定义排序逻辑
};
vectormp1[N]; //正向邻接表
vectormp2[N]; //反向邻接表
int dis[N],vis[N];
void dij(int st,int n,const vector*mp){pqq;              //存放最短路径中可能经过的点for(int i = 1;i<=n;i++){vis[i] = 0;dis[i] = inf;}dis[st] = 0;q.push({st,0});while(!q.empty()){int u = q.top().to;  //当前节点q.pop();if(vis[u])continue;  //如果当前节点来过了就跳过vis[u] = true;for(auto tt:mp[u]){  //遍历下一个节点int v = tt.to;int w = tt.val;if(dis[v]>dis[u]+w){dis[v] = dis[u] + w;    //松弛q.push({v,dis[v]});     //并将下一个点加入}}}
}namespace HH{void solve(){int n,m;cin >> n >> m;while(m--){int u,v,w;cin >> u >> v >> w;mp1[u].push_back({v,w});mp2[v].push_back({u,w});}int ans = 0;dij(1,n,mp1);for(int i = 1;i<=n;i++)ans+=dis[i];dij(1,n,mp2);for(int i = 1;i<=n;i++)ans += dis[i];cout << ans << endl;}inline void main(){IOS// int t;cin  >> t;// while(t--)solve();}
}signed main(){HH::main();AC
}
/*
Input:
5 10
2 3 5
1 5 5
3 5 6
1 2 8
1 3 8
5 3 4
4 1 8
4 5 3
3 5 6
5 4 2Output:
83*/

嗯上面的问题我又优化了一下

void dij(int st,int n,const vector(&mp)[N])

传入vector的时候传地址就不会被再拷贝一遍了，但是因为是二维数组，传入的时候还需要标注大小，要不然编译失败，改完后跑得比原来的好像还要快了（对了N我还偷偷改成1e3+5了）

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！