CNN前置知识:模型的数学符号定义——卷积网络从零实现系列(1)
一、前言：
本系列文章链接：
CNN前置知识:模型的数学符号定义——卷积网络从零实现系列(1)_日拱一两卒的博客-CSDN博客
https://blog.csdn.net/yangwohenmai1/article/details/126951241?spm=1001.2014.3001.5501
CNN前向/反向传播原理推导——卷积网络从零实现系列(2)_日拱一两卒的博客-CSDN博客https://blog.csdn.net/yangwohenmai1/article/details/126622703?spm=1001.2014.3001.5501CNN前向传播源码实现——CNN数学推导及源码实现系列(3)_日拱一两卒的博客-CSDN博客https://blog.csdn.net/yangwohenmai1/article/details/127230225?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22127230225%22%2C%22source%22%3A%22yangwohenmai1%22%7D CNN反向传播源码实现——CNN数学推导及源码实现系列(4)_量化交易领域专家YangZongxian的博客-CSDN博客_cnn网络源码解析CNN算法逻辑、前向和反向传播数学原理、推导过程、以及CNN模型的源码实现上。https://forecast.blog.csdn.net/article/details/127461903?spm=1001.2014.3001.5502
这个CNN系列是博主在学习图像识别过程中的一些学习笔记和总结，包含CNN数学推导和CNN源码实现两部分。属于机器学习的进阶内容，因此本文对神经网络的基础内容不做过多讲解，想学习基础，可看之前的神经网络入门系列文章：人工智能专题研究_日拱一两卒的博客-CSDN博客
本系列重心放在解析CNN算法逻辑、前向和反向传播数学原理、推导过程、以及CNN模型的源码实现上。所以本文作为学习CNN模型理论的前置文章，重点介绍了通用神经网络模型的数学运算表达符号。
大多数包含CNN的网络都属于深度神经网络（Deep Nueral Network），因此简化起见，后续我们都用DNN来表示通用的深度神经网络。
二、DNN前向传播和反向传播中的符号定义
1.单个神经元结构：
首先我们先定义一个基础的神经网络模型，并标注好网络模型会使用的参数符号，以便后续使用和理解。如下图：
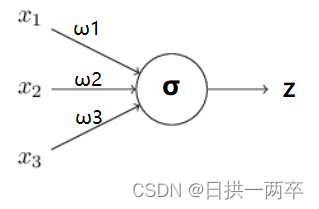
上图表示一个完整的神经元结构，表示输入，
表示权重，
表示激活函数，
表示神经元输出，所以一个完整的表达式形式是
，通常我们会额外添加一个调整系数
，所以另一种简洁的表示形式如下：
2.神经网络结构：
由于DNN层数多，则我们的线性关系系数和偏置
的数量也就是很多了。具体的参数在DNN是如何定义的呢？我们构造一个4层网络如下图：
(1)权重符号
首先我们来看看线性关系系数的定义。以上图这个四层的DNN为例，第二层的第3个神经元到第三层的第2个神经元的线性系数定义为
，即上图标红的这条线。上标3代表权重系数
所在的层数，而下标{2,3}对应的是第三层的第2个神经元索引2和第二层的第3个神经元索引3。你也许会问，为什么不是
, 而是
呢？这主要是为了便于模型用于矩阵表示运算，如果是
而每次进行矩阵运算是
，需要进行转置。将输出的索引放在前面的话，则线性运算不用转置,即直接为
。
总结下，第层的第
个神经元到第
层的第
个神经元的线性系数定义为
。注意，输入层是没有
参数的。
(2)偏置符号
再来看看偏置的定义。还是以这个三层的DNN为例，第二层的偏置定义为
。其中，上标2代表所在的层数。同样的道理，第三层的神经元的偏置应该表示为
。值得注意的是，输入层是没有偏置参数
的。
我们已经介绍了DNN各层线性关系系数，偏置
的定义。假设我们选择的激活函数是
，隐藏层和输出层的输出值为
，则对于下图的三层DNN，利用和感知机一样的思路，我们可以利用上一层的输出计算下一层的输出，也就是所谓的DNN前向传播算法。
(3)输出符号
对于第二层的的输出我们有：
同理对于第三层的的输出，我们有：
将上面的例子一般化，假设第层共有m个神经元，则对于第l层的第
个神经元的输出
，我们有：
其中，如果,则对于的
即为输入层的
。
从上面可以看出，使用代数法一个一个的表示输出比较复杂，而如果使用矩阵法则比较的简洁。假设第层共有
个神经元，而第
层共有
个神经元，则第
层的线性系数
组成了一个
的矩阵
, 第
层的偏置
组成了一个
的向量
, 第
层的的输出
组成了一个
的向量
，第
层的未激活前线性输出
组成了一个
的向量
, 第
层的的输出
组成了一个
的向量
。则用矩阵法表示，第l层的输出为：
这个表示方法简洁漂亮，后面我们的讨论都会基于上面的这个矩阵法表示来。
三、DNN前向传播算法流程的符号描述
有了上一节的数学符号描述，我们后续用符号来描述DNN的前向传播算法也就不难了。所谓的DNN的前向传播算法也就是利用我们的若干个权重系数矩阵,偏置向量
来和输入值向量
进行一系列线性运算和激活运算，从输入层开始一层层的向后计算，一直到运算到输出层，得到输出结果。流程描述如下：
输入: 总层数，所有隐藏层和输出层对应的矩阵
,偏置向量
，输入值向量
输出：输出层的输出
1）初始化
2) for to
, 计算：
最后的结果即为输出。
DNN前向传播的过程很简单，基本都是简单的矩阵乘法和一些激活函数的函数运算，反向传播的过程就会复杂点。
四、DNN反向传播算法推导的符号描述
在进行DNN反向传播算法前，我们需要选择一个损失函数，来度量训练样本计算出的输出和真实的训练样本输出之间的损失。你也许会问：训练样本计算出的输出是怎么得来的？其实这个输出是随机选择一系列并用我们上一节的前向传播算法计算出来的结果。即通过一系列的计算：
。计算到输出层第
层对应的
即为前向传播算法计算出来的输出。
回到损失函数，DNN可选择的损失函数有不少，为了专注算法，这里我们使用最常见的均方差来度量损失。即对于每个样本，我们期望最小化下式：
其中，和
为特征维度为
的向量,而
为
的
范数。损失函数有了，现在我们开始用梯度下降法迭代求解每一层的
。首先是输出层第
层。上街前向传播提到，输出层的
满足下式：
这样对于输出层的参数，我们的损失函数变为：
这样求解,
的梯度就简单了：
注意上式中有一个符号,它代表
积，对于两个维度相同的向量
和,则
。
我们注意到在求解输出层的的时候，有中间依赖部分
也即
，因此我们可以把公共的部分即对
先表示出来，记为：
现在我们终于把输出层的梯度算出来了，那么如何计算上一层L-1层的梯度，上上层L-2层的梯度呢？这里我们需要一步步的递推，注意到对于第l层的未激活输出，它的梯度可以表示为:
如果我们可以依次计算出第层的
,则该层的
很容易计算？为什么呢？上节提到根据前向传播算法，我们有：
所以根据上式我们可以很方便的计算出第层的
,
的梯度如下：
其中，第一个式子的推导可以参考文末参考文献矩阵向量求导链式法则这篇文章中第三节的最后一个公式。那么现在问题的关键就是要求出了。这里我们用数学归纳法，第
层的
上面我们已经求出， 假设第
层的
已经求出来了，那么我们如何求出第l层的
呢？我们注意到：
可见，用归纳法递推和
的关键在于求解
。而
和
的关系其实很容易找出：
这样很容易求出：
将上式带入上面和
关系式，我们得到（矩阵求导后会转置
）：
即：
也可表示为：
现在我们得到了的递推关系式，只要求出了某一层的
，求解
，
的对应梯度就很简单的。
五、DNN反向传播算法流程的符号描述
现在我们总结下DNN反向传播算法的过程。由于梯度下降法有批量（Batch），小批量(mini-Batch)，随机三个变种，为了简化描述，这里我们以最基本的批量梯度下降法为例来描述反向传播算法。实际上在业界使用最多的是mini-Batch的梯度下降法。不过区别仅仅在于迭代时训练样本的选择而已。
输入: 总层数，以及各隐藏层与输出层的神经元个数，激活函数，损失函数，迭代步长
,最大迭代次数MAX与停止迭代阈值
，输入的m个训练样本
输出：各隐藏层与输出层的线性关系系数矩阵和偏置向量
1) 初始化各隐藏层与输出层的线性关系系数矩阵和偏置向量
的值为随机值。
2）for iter to 1 to MAX：
2-1) for to
：
a) 将DNN输入设置为
b) 进行前向传播算法计算
c) 通过损失函数计算输出层的
d) for to 2, 进行反向传播算法计算
2-2) for to
，更新第
层的
:
2-3) 如果所有的变化值都小于停止迭代阈值
，则跳出迭代循环到步骤3。
3） 输出各隐藏层与输出层的线性关系系数矩阵和偏置向量
。
五、总结
本文没用过多篇幅去讲解神经网络的基本原理，而是偏重于使用数学符号对神经网络中数据流转过程进行描述，目的是后续文章介绍CNN模型的基本原理时，可以直接引用本文使用的数学符号，而不至于过于突兀。如果想了解更多关于神经网络的基础知识，可以参考如下连接：人工智能专题研究_日拱一两卒的博客-CSDN博客https://blog.csdn.net/yangwohenmai1/category_9126892.html?spm=1001.2014.3001.5482
本系列下篇文章链接：CNN前向/反向传播原理推导——CNN数学推导及源码实现系列(2)_日拱一两卒的博客-CSDN博客https://blog.csdn.net/yangwohenmai1/article/details/126622703?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22126622703%22%2C%22source%22%3A%22yangwohenmai1%22%7D
参考文献：
机器学习中的矩阵向量求导(四) 矩阵向量求导链式法则 - 刘建平Pinard - 博客园 (cnblogs.com)
Neural networks and deep learning
机器学习中的矩阵向量求导(五) 矩阵对矩阵的求导 - 刘建平Pinard - 博客园 (cnblogs.com)
本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！