leetcode 2212 二维01背包回溯

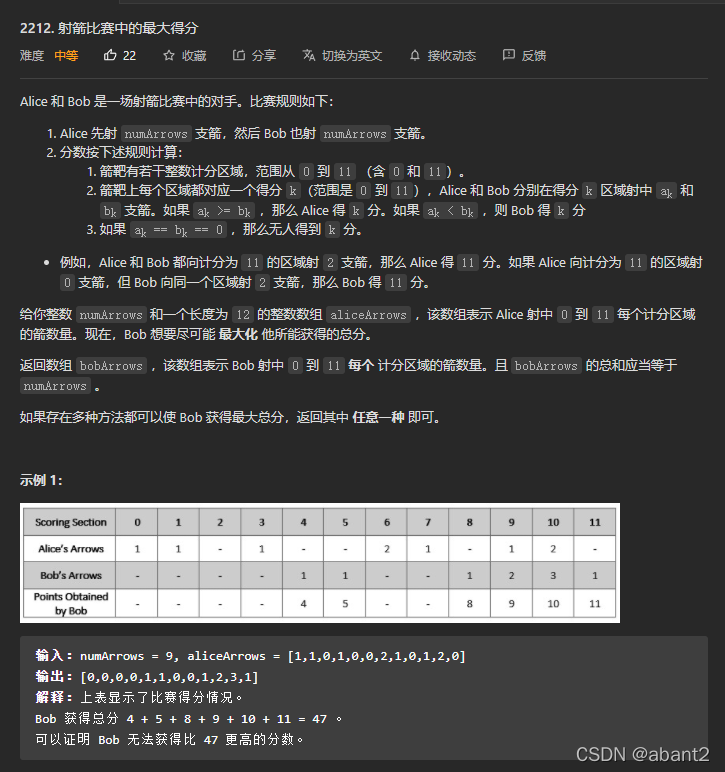
此题要射箭，而且必须比Bob多一支，所以如果决定了要射哪个靶子，那要射的箭的数目是一定的。

所以，我们可以将这个问题转化为01背包问题。注意，此题需要做回溯，而背包做回溯和最长上升子序列不一样，是需要存二维数组然后回溯的。

我们应该知道，一维01背包是由二维背包转化而来的。背包问题的核心是选或者不选，$dp[i][j]$ 表示前i个物品的最佳组合在容量为 $j$ 的背包中取得的最大价值，即$$dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i])$$

其中每件物品我们有选或不选两种选择。

一维01背包只是优化了空间，递推式并不如二维的更鲁棒，在一维中反方向进行递推也只是为了保证空间不变性。

class Solution {
public:vector<int> maximumBobPoints(int numArrows, vector<int>& aliceArrows) {vector<int> v(11), w(11);for(int i=1;i<=11;i++){w[i-1] = aliceArrows[i]+1;v[i-1] = i;}int dp[12][numArrows+1];memset(dp, 0, sizeof(dp));for(int i=1;i<=11;i++){for(int j=0;j<=numArrows;j++){if(w[i-1] > j)dp[i][j] = dp[i-1][j];else dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i-1]]+v[i-1]);}}int mx = 0, mi = 0;// 找到最大价值的背包容量for(int i=0;i<=numArrows;i++){if(dp[11][i] > mx){mx = dp[11][i];mi = i;}}// 回溯得到路径int sum = 0;vector<int> ans(12);for(int i=10;i>=0;i--){if(mi - w[i] < 0)continue;if(dp[i][mi-w[i]]+v[i] == dp[i+1][mi]){ans[i+1] = w[i];mi -= w[i];sum += w[i];}}ans[0] = numArrows-sum;return ans;}
};

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！