医学成像系统2020X射线断层成像仿真实验

实验报告及代码

• 1实验内容
• 2实验内容
• 3实验原理
• • 3.1Randon变换
  • 3.2图像重建
• 4实验步骤
• • 4.1加载仿体断层图像
  • 4.2平行投影
  • 4.3显示投影
  • 4.4图像重建
  • 4.5参数调节及对比分析
• 附：MATLAB代码

1实验内容

（1）掌握X射线计算机断层扫描成像系统的成像原理；
（2）了解并能运用不同断层成像重建的算法；
（3）使用MATLAB代码实现其功能；
（4）进一步掌握X射线断层成像原理。

2实验内容

（1）对一幅仿体断层图像f(x, y)进行平行束扫描；
（2）求投影后的正弦图；
（3）分别利用傅里叶重建法、直接反投影法、滤波反投影法/卷积反投影法对投影后的正弦图进行重建，分别得到重构图像f＇(x, y) ；
（4）比较重构图像f＇(x, y)与原图像f(x, y)的差异，改变实验参数并讨论分析影响重构精度的因素。 

3实验原理

X-CT的实质是基于投影数据重建人体内的断层图像。在CT成像中，物体对X射线的吸收起主要作用，在均匀物体中，X射线的衰减服从指数规律。在X射线穿透人体器官或组织时，由于人体器官或组织是由多种物质成分和不同的密度构成的，所以各点对X射线的吸收系数是不同的。将沿着X射线束通过的物体分割成许多小单元体（体素），令每个体素的厚度均为L。设L足够小，使得每个体素均匀，每个体素的吸收系数为常值，如果X射线的入射强度I0、透射强度I和物体体素的厚度L均为已知，沿着X射线通过路径上的吸收系数之和μ1＋μ2＋……＋μn就可计算出来。

3.1Randon变换

Radon变换是一个积分变换，它将定义在二维平面上的一个函数f(x, y)沿着平面上的任意一条直线做线积分，就相当于对函数f(x, y)做CT扫描。
Radon变换后产生一个极坐标系统，而将𝑝(𝜃)以R-θ直角坐标显示的图像即为正弦图。正弦图可以以图像的方式表示f(x, y)进行变换后的多角度投影数据𝑝(𝑅, 𝜃)。

3.2图像重建

二维图像的投影，就是射线以一定角度穿透物体的衰减值。图像重建的过程包含反投影，就是由这些不同角度（0~180°）下的投影值恢复原始图像。恢复的方法有很多种。下图概括了各种空间的转换关系。

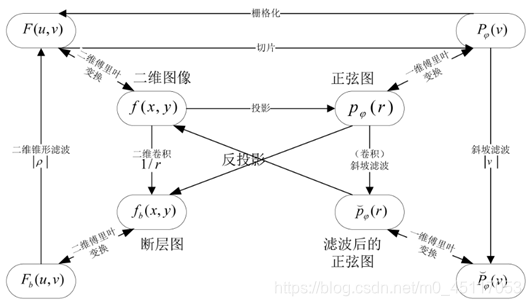
4实验步骤

4.1加载仿体断层图像

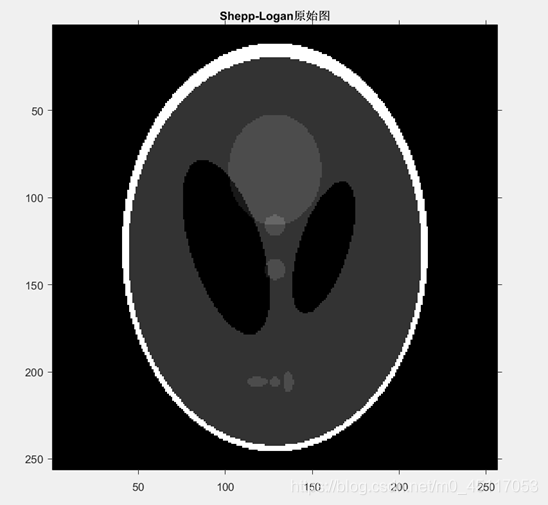
在MATLAB中使用phantom生成头部模型的图像，可用于测试radon和iradon或其他二维重建算法的数值准确性。P是由一个大椭圆（代表大脑）和几个较小的椭圆（代表大脑特征）组成的灰度图像作为原始仿体图像f(x, y)。调用公式如下：
P = phantom(def, n)
其中字符型参数def指定要生成的头部模型的类型，在X射线断层扫描中采用 ‘Modified Shepp-Logan’’，因为Modified Shepp-Logan是Sheep-Logan 幻影的变体，其对比度得到了改进，有更好的视觉效果；并n指定模型图像中的行数和列数，取默认值为256。

4.2平行投影

在MATLAB中编写程序投影。使用如下Radon函数对仿体断层图像f(x, y)进行Radon变换，模拟平行束扫描。
[R,Xp]=radon（I，theta，N）
其中，如果theta是标量，返回R是列向量 ，表示theta角度下图像I的radon变换。如果theta是向量，返回R是矩阵，每一列表示某一theta角度下图像I 的Radon变换。我这里的theta统一使用向量形式。

4.3显示投影

在极坐标系中画投影正弦图。横坐标为ρ，纵坐标为θ。设置投影角度个数为180，每隔1°投影一次。

4.4图像重建

分别利用傅里叶重建法、直接反投影法、滤波反投影法/卷积反投影法对投影后的正弦图进行重建，分别得到重构图像f＇(x, y) 。
在这一部分我统一设置投影角度个数为180，每隔1°投影一次。

4.5参数调节及对比分析

比较重构图像f＇(x, y)与原图像f(x, y)的差异，改变实验参数并讨论分析影响重构精度的因素。
我调节了重建效果较好的Ram-Lak窗函数滤波反投影法的投影参数来观察。
在投影角度非常很大的时候，图像失真严重，如图2和3外形几乎完全变形；在投影角度变小的过程中，逐渐的逼近真实图像的形状，但是有较多的伪影。直到增加到180个投影角度时，在空域的振铃现象减弱，清晰度提高。但是与原图相比还是较为模糊。因此我们可以初步得出结论：
增加投影角度可以使得图像逼近原图；投影方向个数与角度是影响重建图像质量的重要参数。

附：MATLAB代码

clc,clear;%清除P =phantom('Modified Shepp-Logan',256);%P为原图
%Modified Shepp-Logan是Sheep-Logan 幻影的变体，其对比度得到了改进，因此有更好的视觉效果
%画图（取消下一行注释即可画图）
figure,imshow(P),title('Shepp-Logan原始图');%—————————————————————————————————————
%对仿体断层图像f(x,y)进行平行束扫描；画Radon变换后的正弦图
%使用1°增量
theta = 0:1:179;
%对给定的二维矩形数组生成一组平行射线投影
[R2,xp2] = radon(P,theta);
%先转置数组，然后翻转数组
R2 = flipud(R2');
figure,imshow(R2,[],'XData',xp2([1 end]),'YData',[179 0])
%将坐标轴系统的原点由其默认的左上角移到右下角
axis xy
axis on
%设置 X轴为 θ轴， Y 轴为 ρ 轴
xlabel('\rho'),ylabel('\theta')
%显示投影角度0°下的投影曲线
[R22,xp22] = radon(P,theta);
figure
plot(xp22,R22(:,1))
title('theta=0°时的投影曲线')
%—————————————————————————————————————
%%傅里叶重建法
p_N = 256;                  % 图像默认大小256
theta_N = 180;              % 180度平行投影
pad_N = 1024;               % 投影后变为367*180,每列数据就是当前角度下的投影值。367<512，考虑到傅里叶变换时需要基2对齐，故扩展为1024*180theta = 0:1:(theta_N-1);      % 0~180度平行投影
[R,xp] = radon(P,theta);    % R就是投影数据
% 根据每个投影角度下的投影数据，求取其一维傅里叶变换
proj_sino = R;
if mod(length(proj_sino(:,1)),2)==1                       % 如果是奇数个接收栅格，则需要扩展为偶数，填充0proj_sino = [proj_sino;zeros(1,size(proj_sino,2))];    % 填充一行，367*180变为了368*180
end
pad_row = (pad_N-size(proj_sino,1))/2;                    % （1024-368）/2 = 328    
proj_sino = padarray( proj_sino,[pad_row 0],0,'both');    % 368*180，上下填充328行，变为了1024*180
L_pad = pad_row + ceil(((p_N.*sqrt(2)+2)-p_N)/2)+1;       % 原始图像大小为p_N，傅里叶逆变换后为pad_N，则需要截断数据proj_sino = ifftshift(proj_sino,1);                       % 将实际数据移动到两端，中间的是填充的0
f_p = fft(proj_sino,[ ],1);                               % 求取正弦图的一维傅里叶变换，1024*180
f_p = fftshift(f_p,1);                                    % 反向处理，中间的数据移动到两端，两端的数据移动到中间%极坐标栅格化为笛卡尔坐标
nfp = length(f_p(:,1));
omega_sino = (-(nfp-1)/2:(nfp-1)/2).*(2*pi/size(f_p,1));  % 极半径范围 -pi~pi，分成1024等份
theta = theta*pi/180;                                     % 角度转换为弧度，范围0~pi，180等份
[theta_grid, omega_grid] = meshgrid(theta,omega_sino);    % 网格后，theta_grid和omega_grid都是1024*180,theta_grid每一列都是一样的角度，omega_grid每一行都是一样的位置
omega_image = omega_sino;                                               % 根据极半径大小，建立笛卡尔坐标系
[omega_grid_x, omega_grid_y] = meshgrid(omega_image, omega_image);      % 网格后，omega_grid_x和omega_grid_y都是1024*1024，omega_grid_x每一列的x坐标一样，omega_grid_y每一行的y坐标都一样
[coo_th_fft2, coo_r_fft2] = cart2pol(omega_grid_x,omega_grid_y);        % coo_th_fft2 = atan(omega_grid_y/omega_grid_x), coo_r_fft2 = sqrt(omega_grid_y^2+omega_grid_x^2)     
coo_r_fft2 = coo_r_fft2.*sign(coo_th_fft2);                             % 第一象限和第二象限内，笛卡尔半径为负
coo_th_fft2(coo_th_fft2<0) = coo_th_fft2(coo_th_fft2<0) + pi;           % 第二象限和第四象限，笛卡尔角度为0~pi/2；第一象限和第三象限，笛卡尔角度为pi/2~pi
%根据极坐标处的值，二维插值得出笛卡尔坐标处对应的值，插值后也是1024*1024的复数矩阵
Fourier2_radial = interp2(theta_grid,omega_grid,f_p,coo_th_fft2,coo_r_fft2,'cubic',(0+1i.*0));
%根据插值结果，进行二维傅里叶逆变换，得出目标图像 
crop = L_pad;
target = fftshift(ifft2(ifftshift(Fourier2_radial)));                   % 二维傅里叶逆变换，得到的仍然是1024*1024的矩阵
target = target(crop+1:end-crop,crop+1:end-crop);                       % 原始数据大小256*256，因此需要对上面的数据截断
I_a = abs(target);                                                      % 复数的模值 
I_a = (I_a-min(I_a(:)))./(max(I_a(:))-min(I_a(:)));                     % 归一化为 0~1
Lg_I_a = log(1+I_a);                                                    % 为了好的显示效果，取对数
%画图（取消下三行注释即可画图）
figure, suptitle('傅里叶重建法与原图比较');
subplot(1,2,1), imshow(P,[ ]); title('(1)Shepp-Logan原始图')
subplot(1,2,2), imshow(flipud(Lg_I_a),[ ]); title('傅里叶重建法图像')
%—————————————————————————————————————
%直接反投影法&滤波反投影（两种不同的窗函数）
theta3=0:1:179;%180个投影角度每次转动1°
[R3,xp3]=radon(P,theta3);
I31=iradon(R3,0:179,'linear','None');%直接反投影法
I32=iradon(R3,0:179,'linear','Ram-Lak');%使用Ram-Lak窗函数的滤波投影法
I33=iradon(R3,0:179,'linear','Hamming');%使用Hamming窗函数的滤波投影法
%画图（取消下5行注释即可画图）
figure,suptitle('直接投影法和滤波反投影法与原图比较');
subplot(2,2,1),imshow(P),title('(1)Shepp-Logan原始图') ;
subplot(2,2,2),imshow(I31,[]),title('(2)直接反投影法');
subplot(2,2,3),imshow(I32),title('(3)滤波反投影法(Ram-Lak)');
subplot(2,2,4),imshow(I33),title('(4)滤波反投影法(Hamming)');%—————————————————————————————————————
%改变投影角度，测试滤波反投影法测重建效果
theta40=0:36:144;
[R40,xp4] = radon(P,theta40);%5个投影角度每次转动36°
theta41=0:18:162;
[R41,xp4] = radon(P,theta41);%10个投影角度每次转动18°
theta42 = 0:10:170;
[R42,xp4] = radon(P,theta42);%18个投影角度每次转动10°
theta43 = 0:5:175;
[R43,xp4] = radon(P,theta43);%36个投影角度每次转动5°
theta44 = 0:1:179;
[R44,xp4] = radon(P,theta44);%180个投影角度每次转动1°
I40=iradon(R40,36,'linear','Ram-Lak');
I41=iradon(R41,18,'linear','Ram-Lak');
I42=iradon(R42,10,'linear','Ram-Lak');
I43=iradon(R43,5,'linear','Ram-Lak');
I44=iradon(R44,1,'linear','Ram-Lak');
%画图（取消下面7行注释即可画图）
figure,suptitle('滤波反投影法参数调节');
subplot(2,3,1),imshow(P),title('(1)Shepp-Logan原始图') ;
subplot(2,3,2),imshow(I40),title('(2)5个投影角度每次转动36°');
subplot(2,3,3),imshow(I41),title('(3)10个投影角度每次转动18°');
subplot(2,3,4),imshow(I42),title('(4)18个投影角度每次转动10°');
subplot(2,3,5),imshow(I43),title('(5)36个投影角度每次转动5°');
subplot(2,3,6),imshow(I44),title('(6)180个投影角度每次转动1°');

参考
[1]https://ww2.mathworks.cn/help/images/ref/phantom.html
[2]庄天戈.CT原理与算法[M].上海:上海交通大学出版社，1992:33,31,25,30

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！