[leetcode] Python(14)--对角线遍历(498)、螺旋矩阵(54)、杨辉三角(118)、二进制求和(67)

从零开始的力扣（第十四天）~

1.对角线遍历

给定一个含有 M x N 个元素的矩阵（M 行，N 列），请以对角线遍历的顺序返回这个矩阵中的所有元素，对角线遍历如下图所示。

示例:
输入:
[[ 1, 2, 3 ],
[ 4, 5, 6 ],
[ 7, 8, 9 ]]

输出: [1,2,4,7,5,3,6,8,9]

解释:

说明:
给定矩阵中的元素总数不会超过 100000 。
—————————————————————————————————————————

通过观察结果可知元素坐标的变化与矩阵大小有关，需要判断什么时候增加横坐标，什么时候增加纵坐标

class Solution(object):def findDiagonalOrder(self, matrix):""":type matrix: List[List[int]]:rtype: List[int]"""res = []if matrix == []:return resm = len(matrix)#行n = len(matrix[0])#列top = Truenum = i = j = 0while num<m*n:res.append(matrix[i][j])num += 1if num == m*n:breakif top:if j == n-1:i += 1top = Falseelif i == 0:j += 1top = Falseelse:i-=1j+=1else:if i == m-1:j +=1top = Trueelif j==0:i += 1top =Trueelse:j-=1i+=1return res

还有一种理解方法，可以看出每一层元素横纵坐标和相等，只是奇数层与偶数层坐标计数方式相反

每层的索引和相等：
1. 假设矩阵无限大；
2. 索引和为{偶}数，向上遍历，{横}索引值递减，遍历值依次是(x,0),(x-1,1),(x-2,2),...,(0,x)
3. 索引和为{奇}数，向下遍历，{纵}索引值递减，遍历值依次是(0,y),(1,y-1),(2,y-2),...,(y,0)每层的索引和:0:              (00)1:            (01)(10)2:          (20)(11)(02)3:        (03)(12)(21)(30)4:      (40)(31)(22)(13)(04)5:    (05)(14)(23)(32)(41)(50)6:  (60)(51)................(06)按照“层次”遍历，依次append在索引边界内的值即可

这里有一个循环实现，但是无奈当矩阵过大时，时间会超出限制，这里不能使用，下面放下代码：

class Solution(object):def findDiagonalOrder(self, matrix):""":type matrix: List[List[int]]:rtype: List[int]"""m = len(matrix) - 1     # 横轴 索引最大值 mn = len(matrix[0]) - 1  # 纵轴 索引最大值 nc = m + n + 1           # 层数 等于 横纵最大索引之和 + 1l = []for x in range(c+1):    # 每层的横纵索引之和相等，刚好等于 层数值+1if x % 2 == 0:      # 索引和为{偶}数，向上遍历，{横}索引值递减，遍历值依次是(x,0),(x-1,1),(x-2,2),...,(0,x)，不要索引出界的，即可for i in range(x,-1,-1):j = x - iif i <= m and j <= n:l.append(matrix[i][j])elif j > n:breakelse:continueelse:                # 索引和为{奇}数，向下遍历，{纵}索引值递减，遍历值依次是(0,y),(1,y-1),(2,y-2),...,(y,0)，不要索引出界的，即可for j in range(x, -1, -1):i = x - jif i <= m and j <= n:l.append(matrix[i][j])elif i > m:breakelse:continuereturn l

2.螺旋矩阵

给定一个包含 m x n 个元素的矩阵（m 行, n 列），请按照顺时针螺旋顺序，返回矩阵中的所有元素。

示例 1:
输入:
[
[ 1, 2, 3 ],
[ 4, 5, 6 ],
[ 7, 8, 9 ]
]
输出: [1,2,3,6,9,8,7,4,5]

示例 2:
输入:
[
[1, 2, 3, 4],
[5, 6, 7, 8],
[9,10,11,12]
]
输出: [1,2,3,4,8,12,11,10,9,5,6,7]
—————————————————————————————————————————

最开始的想法，设置4个限定参数，i_min，i_max，j_min，j_max，对矩阵进行螺旋搜索，但是这样的限定条件很复杂，并且会出现很多特殊情况

class Solution(object):def spiralOrder(self, matrix):""":type matrix: List[List[int]]:rtype: List[int]"""if not matrix:return []i_max = m = len(matrix) - 1j_max = n = len(matrix[0]) - 1 i_min = j_min = 0l = []for x in range(min((m + 1) / 2 + 1, (n + 1) / 2 + 1)):if j_max >= j_min:for j in range(j_min, j_max + 1):l.append(matrix[i_min][j])i_min += 1if i_max >= i_min:for i in range(i_min, i_max + 1):l.append(matrix[i][j_max])j_max -= 1if j_max >= j_min:for j in range(j_max, j_min - 1, -1):l.append(matrix[i_max][j])i_max -= 1if i_max >= i_min:for i in range(i_max, i_min - 1, -1):l.append(matrix[i][j_min])j_min += 1else:breakelse:breakelse:breakelse:breakreturn l

也是螺旋搜索，但是会将搜索后的一行或一列删除，这样能大大加快速度并且易于写限制条件

class Solution:def spiralOrder(self, matrix):""":type matrix: List[List[int]]:rtype: List[int]"""round = 1 # 1上 2右 3下 4左output = []if matrix == []:return outputwhile(len(matrix) != 0):# 若为1 先插入第一行，后删除第一行if round % 4 == 1:round +=1    output.extend(matrix[0])del matrix[0]# 若为2 先插入最右列，后删除最右列elif round % 4 == 2:round +=1if len(matrix[0])!= 0: v = [x[-1] for x in matrix]  output.extend(v)for i in range(len(matrix)):del matrix[i][-1]# matrix[i].pop(-1)# 若为3 先插入最后一行，后删除最后一行elif round % 4 == 3:round +=1matrix[-1].reverse()output.extend(matrix[-1])del matrix[-1]# 若为4 先插入最左列，后删除最左列elif round % 4 == 0:round +=1if len(matrix[0])!= 0: v = [x[0] for x in matrix] v.reverse()output.extend(v)for i in range(len(matrix)):del matrix[i][0]# matrix[i].pop(0)return output

最好也是最易于思考的方法：取矩阵的第一行并删除，之后将矩阵逆时针选装90度，接着循环

class Solution(object):def spiralOrder(self, matrix):""":type matrix: List[List[int]]:rtype: List[int]"""# 取首行，去除首行后，对矩阵翻转来创建新的矩阵，# 再递归直到新矩阵为[],退出并将取到的数据返回ret = []if matrix == []:return retret.extend(matrix[0]) # 上侧new = [reversed(i) for i in matrix[1:]]if new == []:return retr = self.spiralOrder([i for i in zip(*new)])ret.extend(r)return ret

具体旋转操作可以看之前的leecode旋转矩阵那道题。

3.杨辉三角

给定一个非负整数 numRows，生成杨辉三角的前 numRows 行。

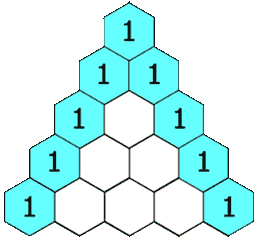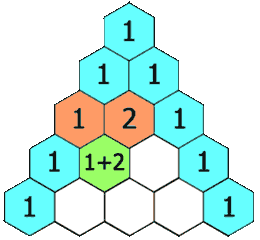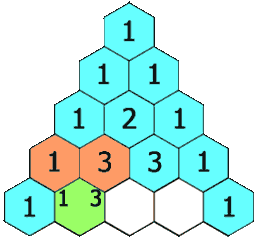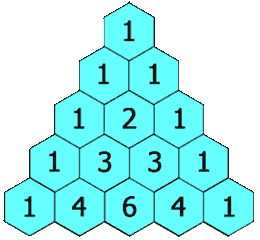
在杨辉三角中，每个数是它左上方和右上方的数的和。

示例:
输入: 5
输出:
[
[1],
[1,1],
[1,2,1],
[1,3,3,1],
[1,4,6,4,1]
]
—————————————————————————————————————————

高中的知识，杨辉三角的每个数就是 C m n C_m^n Cmn​，只需要写一个阶乘算法就行

class Solution(object):def generate(self, numRows):""":type numRows: int:rtype: List[List[int]]"""output = []def factorial(n):if n == 0 or n == 1:return 1else:return (n*factorial(n-1))for i in range(numRows):list_row = []for j in range(i + 1):list_row.append(factorial(i)/factorial(i - j)/factorial(j))output.append(list_row) return output

这道题就是很明显的动态规划了，直接规划起来

class Solution(object):def generate(self, numRows):""":type numRows: int:rtype: List[List[int]]"""result = []for i in range(numRows):now = [1]*(i+1)if i >= 2:for n in range(1,i):now[n] = pre[n-1]+pre[n]result += [now]pre = nowreturn result

4.二进制求和

给定两个二进制字符串，返回他们的和（用二进制表示）。

输入为非空字符串且只包含数字 1 和 0。

示例 1:
输入: a = “11”, b = “1”
输出: “100”

示例 2:
输入: a = “1010”, b = “1011”
输出: “10101”
—————————————————————————————————————————

转换为十进制求和再转换回去

class Solution(object):def addBinary(self, a, b):""":type a: str:type b: str:rtype: str"""return bin(int(a,2) + int(b,2)).replace('0b','')

其中bin()是十进制转换为二进制，而且前缀有"0b"，需要替换掉，orc()是十进制转换为八进制，hex()是十进制转换为十六进制，这几个转换输入为int，输出都为str，而int()可以将所有进制转换为十进制只用将尾缀换为2，8，16即可，而int输入则必须为str，需要记住。

将串内数字进行进位的加法（我觉得这才是题目要求的?）

class Solution:def addBinary(self, a, b):""":type a: str:type b: str:rtype: str"""res = []temp = str(int(a)+int(b))for i in range(len(temp)-1,-1,-1):res.append(int(temp[i]))res.append(0)for i in range(len(res)):if res[i]>=2:res[i] = res[i]-2res[i+1] = res[i+1]+1res.reverse()s = ''for i in res:s = s + str(i)return str(int(s))

以上就是今日经验！

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！