杨辉三角Ⅱ

目录

一、需求

二、递归法

2.1  思路分析

2.2  代码实现

2.3  复杂度分析

三、数组法

3.1  思路分析

3.2  代码实现

3.3  代码优化

3.4  复杂度分析

四、公式法

4.1  思路分析

4.2  代码实现

4.3  代码优化

4.4  复杂度分析

五、参考地址

一、需求

      A:给定一个非负索引k，其中k<=33，返回杨辉三角的第k行；

二、递归法

2.1  思路分析

      A:首先新建两个List对象,其中一个当作中间变量来储存某行数据;

      B:若k==0，直接将1存到集合，并返回集合;

      C:递归结束条件,k=1时，将两个1存储到集合，并返回;

      D:递归规律，row = getRow(k-1);

      E:当最底层递归结束后，此时k=2,要存储第2行，然后回溯到k=3,存储第3行，直到k行全部存储完毕;

      F:返回集合对象；

2.2  代码实现

public List getRow(int rowIndex) {//创建对象List triangle = new ArrayList();List row = new ArrayList();//递归结束条件if(rowIndex == 0) {row.add(1);return row;}if(rowIndex == 1) {row.add(1);row.add(1);return row;}//开始递归row = getRow(rowIndex - 1);triangle.add(1);for(int j = 1; j < rowIndex; j++) {triangle.add(row.get(j-1)+row.get(j));}triangle.add(1);return triangle;}

2.3  复杂度分析

      A:时间复杂度为O(rowIndex)；

      B:空间复杂度，有2个集合对象和递归，O(3rowIndex)，待议待议；

三、数组法

3.1  思路分析

      A:创建一个集合对象row存储要返回的行数据;

      B:集合的第一个元素存入1;

      C:利用循环,外层循环从1到k，内层循环表示在当前行的条件下，要计算的次数;

      D:内循环结束后，集合的最后一个元素存入1，然后继续外循环;

      E:外循环结束后，返回集合;

3.2  代码实现

public List getRow(int rowIndex) {//创建集合对象List row = new ArrayList();//创建中间变量int pre = 1;//集合第一个元素置1row.add(1);//每次循环结果的结果对应第i行的数据//pre很好的利用了首尾都是1，每次循环结束后，因为遍历到temp=1，pre会置1;//每次循环开始时，pre=1,然后取第2个元素，把和覆盖第2个元素，然后更新pre为第2个元素覆盖之前的值;//一直更新到pre=1，也就加完了，最后添上1;for(int i = 1; i <= rowIndex; i++) {for(int j = 1; j < i; j++) {int temp = row.get(j);row.set(j,pre+row.get(j));pre = temp;}row.add(1);}return row;}

3.3  代码优化

//把数据从后往前存储
public List getRow(int rowIndex) {//创建集合对象List row = new ArrayList();//添加元素row.add(1);//开始循环for(int i = 1; i <= rowIndex; i++) {for(int j = i-1; j >0; j--) {row.set(j,row.get(j-1)+row.get(j));}row.add(1);}return row;}

3.4  复杂度分析

      A:时间复杂度为O(rowIndex^2)；

      B:空间复杂度为O(rowIndex)；

四、公式法

4.1  思路分析

4.2  代码实现

public List getRow(int rowIndex) {//创建集合对象List row = new ArrayList();for(int k = 0; k <= rowIndex; k++) {row.add(combination(rowIndex,k));}return row;}//求组合的值public int combination(int rowIndex,int k) {long res = 1;for(int i = 1; i <= k; i++) {res = res * (rowIndex-k+i) / i;}return (int)res;}

4.3  代码优化

       A:关于Cnk的求解，对公式进行化简；

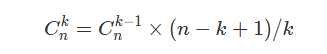
public List getRow(int rowIndex) {List row = new ArrayList<>();int N = rowIndex;//pre用于更新Cn(k-1);//假设N=2,那么pre一开始为1，相当于C2(0)，根据公式求出C2(1)，加到集合里;//然后pre更新为C2(1),然后又利用公式求出C2(2)，加到集合里，pre更新为C2(2)，也就是重置为1;//此时集合里的元素是1 2 1;long pre = 1;row.add(1);//因为Cn(0)都为2，故k从1开始到Nfor (int k = 1; k <= N; k++) {long cur = pre * (N - k + 1) / k;row.add((int) cur);pre = cur;}return row;
}

4.4  复杂度分析

      A:时间复杂度为O(rowIndex)；

      B:空间复杂度为O(rowIndex)；

五、参考地址

      A:https://leetcode-cn.com/problems/pascals-triangle-ii/solution/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-by--28/

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！