《视觉SLAM十四讲从理论到实践 第二版》课后习题——ch3
1. 验证旋转矩阵是正交矩阵。

2. * 寻找罗德里格斯公式的推导过程并加以理解。

3. 验证四元数旋转某个点后,结果是一个虚四元数(实部为零),所以仍然对应到一个三维空间点,见式(3.33)。
证明需要用到四元数的乘法以及乘法的两个推论,四元数乘法以及推论证明如下:

接下来证明旋转变换后结果是虚四元数,实部为0,虚部为罗德里格斯公式结果:


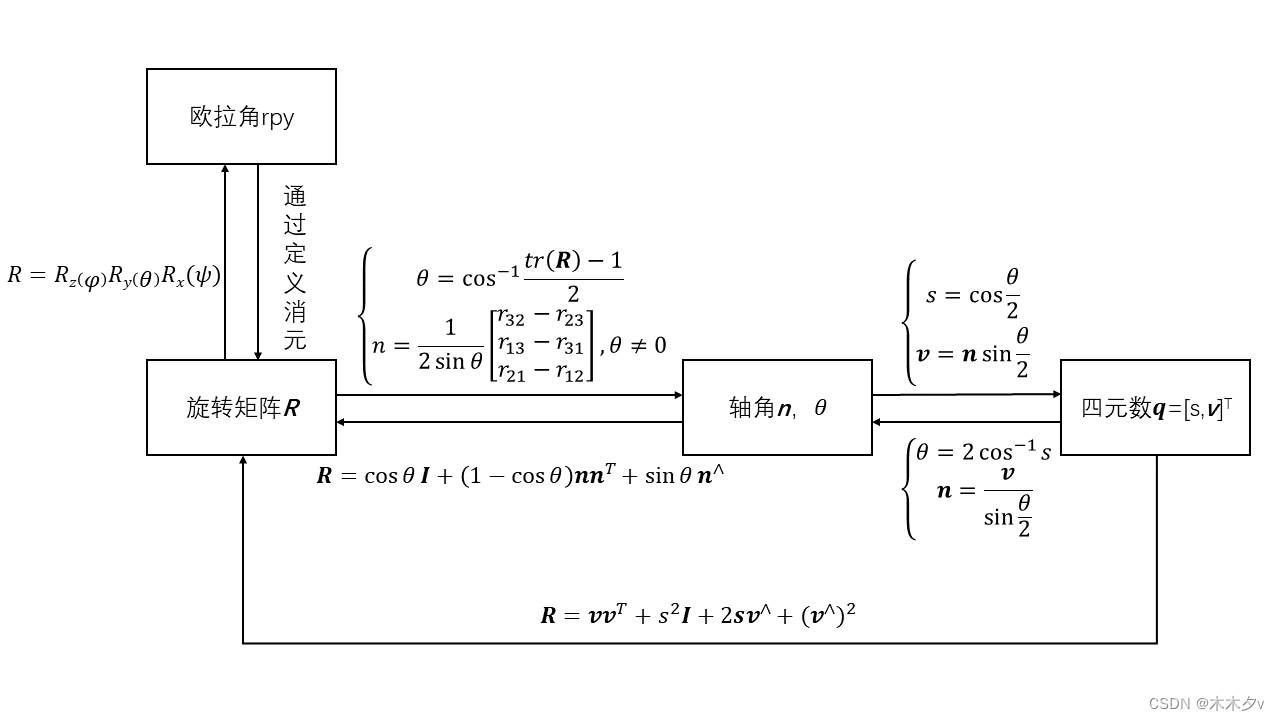
4. 画表总结旋转矩阵、轴角、欧拉角、四元数的转换关系。
5. 假设有一个大的 Eigen 矩阵,想把它的左上角 3 × 3 的块取出来,然后赋值为 。请编程实现。
。请编程实现。
#include//包含Eigen头文件
#include
#include#define MATRIX_SIZE 100
using namespace std;int main(int argc,char **argv)
{//设置输出小数点后3位cout.precision(3);Eigen::Matrix matrix_NN = Eigen::MatrixXd::Random(MATRIX_SIZE,MATRIX_SIZE);Eigen::Matrixmatrix_33 = Eigen::MatrixXd::Random(3,3);//3x3矩阵变量
/*方法1:循环遍历矩阵的三行三列 */
/*cout<<"提取出来的矩阵块为:"< 6. * 一般线程方程 Ax = b 有哪几种做法?你能在 Eigen 中实现吗?
参考该链接
#include
#include
#include
#include
/*线性方程组Ax = b的解法(直接法(1,2,3,4,5)+迭代法(6))其中只有2 3方法不要求方程组个数与变量个数相等*///包含Eigen头文件
//#include
#include
#include
#include //下面这两个宏的数值一样的时候 方法1 4 5 6才能正常工作
#define MATRIX_SIZE 3 //方程组个数
#define MATRIX_SIZE_ 3 //变量个数
//using namespace std;
typedef Eigen::Matrix Mat_A;
typedef Eigen::Matrix Mat_B;//Jacobi迭代法的一步求和计算
double Jacobi_sum(Mat_A &A,Mat_B &x_k,int i);//迭代不收敛的话 解向量是0
Mat_B Jacobi(Mat_A &A,Mat_B &b, int &iteration_num, double &accuracy );int main(int argc,char **argv)
{//设置输出小数点后3位std::cout.precision(3);//设置变量Eigen::Matrix matrix_NN = Eigen::MatrixXd::Random(MATRIX_SIZE,MATRIX_SIZE_);Eigen::Matrix v_Nd = Eigen::MatrixXd::Random(MATRIX_SIZE,1);//测试用例matrix_NN << 10,3,1,2,-10,3,1,3,10;v_Nd <<14,-5,14;//设置解变量Eigen::Matrixx;//时间变量clock_t tim_stt = clock();/*1、求逆法 很可能没有解 仅仅针对方阵才能计算*/
#if (MATRIX_SIZE == MATRIX_SIZE_)x = matrix_NN.inverse() * v_Nd;std::cout<<"直接法所用时间和解为:"<< 1000*(clock() - tim_stt)/(double)CLOCKS_PER_SEC<<"MS"<< std::endl << x.transpose() << std::endl;
#elsestd::cout<<"直接法不能解!(提示:直接法中方程组的个数必须与变量个数相同,需要设置MATRIX_SIZE == MATRIX_SIZE_)"<es(B);EV = es.eigenvalues();
// cout<<"迭代矩阵特征值为:"< __complex_abs(EV(index)) )?maxev:(__complex_abs(EV(index)));}std::cout<< "Jacobi迭代矩阵的谱半径为:"<< maxev<= 1){std::cout<<"Jacobi迭代算法不收敛!"< R )R = temp;}//判断进度是否达到精度要求 达到进度要求后 自动退出if( R < accuracy ){std::cout <<"Jacobi迭代算法迭代"<< k << "次达到精度要求."<< std::endl;isFlag = 1;break;}//清零R,交换迭代解R = 0;x_k = x_k1;}if( !isFlag )std::cout << std::endl <<"迭代"< 本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!