基于MATLAB机电系统动态仿真部分习题

MATLAB仿真部分习题

• 习题2：第1~8题
• 习题5：第1~7题
• 习题6：第2~4题

习题2：第1~8题

第1题

在指令窗口输入： x = 1:0.2:2 和 y = 2:0.2:1 ，观察所生成的数组。

代码实现：

 x = 1:0.2:2y = 2:0.2:1

运行结果：

x =1.0000    1.2000    1.4000    1.6000    1.8000    2.0000y =空的 1×0 double 行向量

第2题

要求在[ 0 , 2π ]上产生50个等距采样数据的一维数组，试用两种不同的指令实现。

代码实现：

x1 = 0:2*pi/9:2*pi;%冒号生成法
x2 = linspace(0,2*pi,10);%线性定点法

运行结果：

>> x1x1 =0    0.6981    1.3963    2.0944    2.7925    3.4907    4.1888    4.8869    5.5851    6.2832>> x2x2 =0    0.6981    1.3963    2.0944    2.7925    3.4907    4.1888    4.8869    5.5851    6.2832

第3题

计算
e − 2 t s i n t . \\e^{-2t}sint\,. e−2tsint.
其中，t 为 [ 0 , 2π ]上生成的10个等距采样的数组。

代码实现：

 t = linspace(0,2*pi,10);t1 = exp(-2*t).*sin(t);

运行结果：

>> tt =0    0.6981    1.3963    2.0944    2.7925    3.4907    4.1888    4.8869    5.5851    6.2832>> t1t1 =0    0.1591    0.0603    0.0131    0.0013   -0.0003   -0.0002   -0.0001   -0.0000   -0.0000

第4题

已知

计算矩阵A 、B乘积和点乘。

代码实现：

 A = [1,2;3,4];B = [5,6;7,8];A1 = A * B;B1 = A .* B;

运行结果：

>> A1A1 =19    2243    50>> B1B1 =5    1221    32

第5题

对题4中的 A，令 A ( : , 3 ) = [ 5 ,6 ] 生成 2×3 数组 ， 利用 reshape ( A , 3 , 2) 指令，使A重构为 3×2 数组，再利用 “[ ]” ，裁去重构后的数组 A 的第一列 ，求最后结果。

代码实现：

 A = [1,2;3,4];A(:,3) = [5;6];reshape(A,3,2);A(:,1) = [];

运行结果：

>> AA =2     54     6

第6题

已知

计算 A & B ，A | B ，~A ，A == B , A > B 。

代码实现：

A = [0,2,3,4;1,3,5,0];
B = [1,0,5,3;1,5,0,5];
X1 = A & B;
X2 = A | B;
X3 = ~A;
X4 = (A == B);
X5 = (A>B);

运行结果：

>> X1X1 =2×4 logical 数组0   0   1   11   1   0   0>> X2X2 =2×4 logical 数组1   1   1   11   1   1   1>> X3X3 =2×4 logical 数组1   0   0   00   0   0   1>> X4X4 =2×4 logical 数组0   0   0   01   0   0   0>> X5X5 =2×4 logical 数组0   1   0   10   0   1   0

第7题

先产生一个 3×3 的正态随机矩阵 A , 再用 floor(A) 、ceil(A) 、fix(A) 、round(A)，进行 A 的取整运算，体会不同取整方法的效果。

代码实现：

A1 = rand(3);%返回3*3的随机矩阵
A = 10 + 2*A1;%产生均值为10，方差为4的矩阵
X1 = floor(A);
X2 = ceil(A);
X3 = fix(A);
X4 = round(A);

运行结果：

>> X1X1 =11    11    1011    11    1110    10    11>> X2X2 =12    12    1112    12    1211    11    12>> X3X3 =11    11    1011    11    1110    10    11>> X4X4 =12    12    1112    11    1110    10    12

第8题

将题6中的 A阵 用串转换函数转换为串B，再用size指令查看两者的结构有何不同。

代码实现：

  A = [0,2,3,4;1,3,5,0];%得到题6的A矩阵B = num2str(A);Y1 = size(A);Y2 = size(B);

运行结果：

>> Y1Y1 =2     4>> Y2Y2 =2    10

习题5：第1~7题

第1题

将下列系统的传递函数模型用MATLAB语言表达出来。

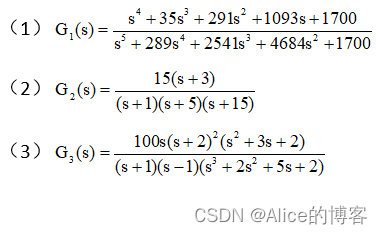
代码实现：

 %习题5,第1题(1):传递函数模型(有理多项式)num = [1,35,291,1093,1700];den = [1,289,254,2541,4684,1700];sys = tf(num,den);

运行结果：

>> syssys =s^4 + 35 s^3 + 291 s^2 + 1093 s + 1700--------------------------------------------------s^5 + 289 s^4 + 254 s^3 + 2541 s^2 + 4684 s + 1700Continuous-time transfer function.

代码实现：

  %习题5,第1题(2)：零-极点模型z = -3;p = [-1,-5,-15];k = 15;sys = zpk(z,p,k);

运行结果：

>> syssys =15 (s+3)------------------(s+1) (s+5) (s+15)Continuous-time zero/pole/gain model.

代码实现：

%习题5,第1题(3)：两个传递函数串联z = [0,-2,-2];p = [-1,1];k = 100;[num1,den1] = zp2tf(z',p,k);sys1 = tf(num1,den1);num = [1,3,2];den = [1,2,5,2];sys2 = tf(num,den);sys = series(sys1,sys2);

运行结果：

>> syssys =100 s^5 + 700 s^4 + 1800 s^3 + 2000 s^2 + 800 s-----------------------------------------------s^5 + 2 s^4 + 4 s^3 - 5 s - 2Continuous-time transfer function.

第2题

求第 1 题中各个系统模型的等效状态空间模型。

代码实现：

 %习题5,第2题(1):传递函数模型→状态空间模型num = [1,35,291,1093,1700];den = [1,289,254,2541,4684,1700];sys = tf(num,den);Gss = ss(sys);

运行结果：

>> GssGss =A = x1      x2      x3      x4      x5x1    -289  -15.88  -9.926  -4.574   -1.66x2      16       0       0       0       0x3       0      16       0       0       0x4       0       0       4       0       0x5       0       0       0       1       0B = u1x1   2x2   0x3   0x4   0x5   0C = x1      x2      x3      x4      x5y1     0.5   1.094  0.5684  0.5337  0.8301D = u1y1   0Continuous-time state-space model.

代码实现：

 %习题5,第2题(2)：零-极点模型→传递函数模型→状态空间模型z = -3;p = [-1,-5,-15];k = 15;[num,den] = zp2tf(z,p,k);sys = tf(num,den);Gss = ss(sys);

运行结果：

>> GssGss =A = x1      x2      x3x1     -21  -11.88  -2.344x2       8       0       0x3       0       4       0B = u1x1   2x2   0x3   0C = x1      x2      x3y1       0  0.9375  0.7031D = u1y1   0Continuous-time state-space model.

代码实现：

%习题5,第2题(3)：两个传递函数串联，状态空间模型z = [0,-2,-2];p = [-1,1];k = 100;[num1,den1] = zp2tf(z',p,k);sys1 = tf(num1,den1);num = [1,3,2];den = [1,2,5,2];sys2 = tf(num,den);sys = series(sys1,sys2);Gss = ss(sys);

运行结果：

>> GssGss =A = x1    x2    x3    x4    x5x1    -2    -2     0  1.25     1x2     2     0     0     0     0x3     0     1     0     0     0x4     0     0     2     0     0x5     0     0     0   0.5     0B = u1x1  64x2   0x3   0x4   0x5   0C = x1     x2     x3     x4     x5y1  7.813  10.94  15.63  5.078  1.563D = u1y1  100Continuous-time state-space model.

第3题

将以下系统状态空间模型用MATLAB语言表达出来。

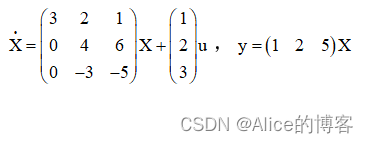
代码实现：

%习题5,第3题：状态空间模型A = [3,2,1;0,4,6;0,-3,-5];B = [1,2,3]';C = [1,2,5];D = 0;Gss = ss(A,B,C,D);

运行结果：

>> GssGss =A = x1  x2  x3x1   3   2   1x2   0   4   6x3   0  -3  -5B = u1x1   1x2   2x3   3C = x1  x2  x3y1   1   2   5D = u1y1   0Continuous-time state-space model.

第4题

求第 3 题中的系统模型的等效传递函数模型和零极点模型。

代码实现：

%习题5,第4题：状态空间模型→传递函数模型,传递函数模型→零-极点模型A = [3,2,1;0,4,6;0,-3,-5];B = [1,2,3]';C = [1,2,5];D = 0;Gss = ss(A,B,C,D);[num,den] = ss2tf(A,B,C,D);sys = tf(num,den);Gzpk = zpk(sys);

运行结果：

>> syssys =20 s^2 - 83 s + 138---------------------s^3 - 2 s^2 - 5 s + 6Continuous-time transfer function.>> GzpkGzpk =20 (s^2 - 4.15s + 6.9)----------------------(s+2) (s-3) (s-1)Continuous-time zero/pole/gain model.

第5题

已知系统动力学方程如下，试用MATLAB语言写出它们的传递函数。

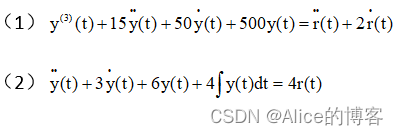
代码实现：

%习题5,第5题(1)：传递函数模型
num = [1,2,0];
den = [1,15,50,500];
sys = tf(num,den);

运行结果：

>> syssys =s^2 + 2 s-------------------------s^3 + 15 s^2 + 50 s + 500Continuous-time transfer function.

代码实现：

%习题5,第5题(2)：传递函数模型
num = [4,0];
den = [1,3,6,4];
sys = tf(num,den);

运行结果：

>> syssys =4 s---------------------s^3 + 3 s^2 + 6 s + 4Continuous-time transfer function.

第6、7题

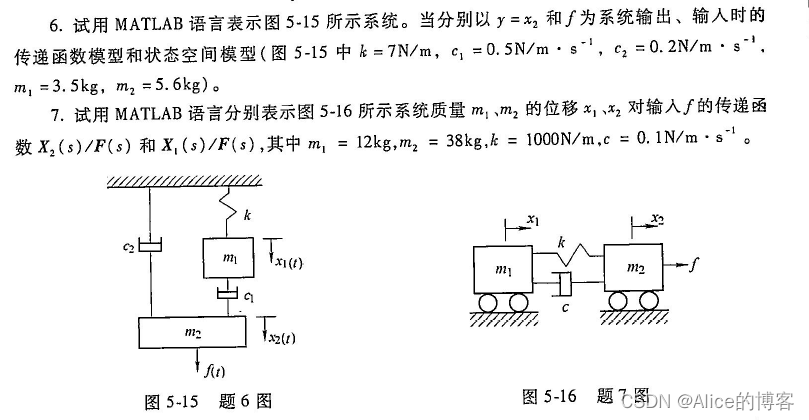
代码实现：

%习题5,第6题：传递函数模型
k = 7;
c1 = 0.5;
c2 = 0.2;
m1 = 3.5;
m2 = 5.6;
num = [m1,c1,k];
den = [m1*m2,c1*m1+c2*m1+c1*m2,c1*c2+m2*k,c1*k+c2*k,0];
sys = tf(num,den);

运行结果：

>> syssys =3.5 s^2 + 0.5 s + 7--------------------------------------19.6 s^4 + 5.25 s^3 + 39.3 s^2 + 4.9 sContinuous-time transfer function.

代码实现：

%习题5,第7题：传递函数模型
m1 = 12;
m2 = 38;
k = 1000;
c = 0.1;
num = [c,k];
den = [m1*m2,m1*c+m2*c,m1*k+m2*k,0,0];
sys1 = tf(num,den);num1 = [m1,c,k];
den = [m1*m2,m1*c+m2*c,m1*k+m2*k,0,0];
sys2 = tf(num1,den);

运行结果：

>> sys1sys1 =0.1 s + 1000---------------------------456 s^4 + 5 s^3 + 50000 s^2Continuous-time transfer function.>> sys2sys2 =12 s^2 + 0.1 s + 1000---------------------------456 s^4 + 5 s^3 + 50000 s^2Continuous-time transfer function.

习题6：第2~4题

第2题

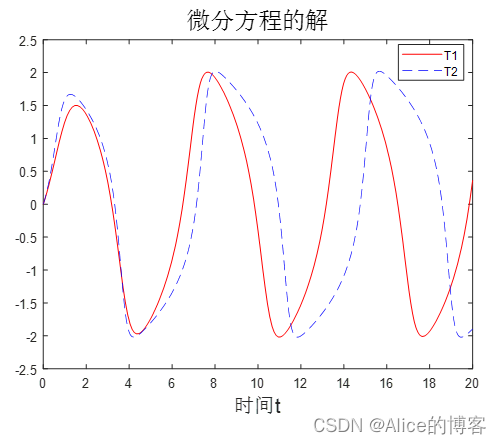
将例 6-2 中的微分方程改写为以下形式：

求 u 分别为1、2时，在时间区间 t = [ 0 , 20 ] 微分方程的解（提示：使用附加变量的ode算法）

代码实现：

 %习题6,第2题，主函数tspan = [0,20];x0 = [0,1];ps = 1;[T1,X1] = ode45('wffc',tspan,x0,odeset,ps);ps = 2;[T2,X2] = ode45('wffc',tspan,x0,odeset,ps);plot(T1,X1(:,1),'r',T2,X2(:,1),'b--');title('微分方程的解','fontsize',18);xlabel('时间t','fontsize',15);legend('T1','T2');

 %习题6,第2题，子函数
function dx = wffc(t,x,flag,ps)
%微分方程的解dx = zeros(2,1);
dx(1) = x(2);
dx(2) = ps*(1-x(1)^2)*x(2)-x(1);end

运行结果：

第3、4题

代码实现：

%习题6,第3题(1)
num = [1,0.5];
den = [1,0.1];
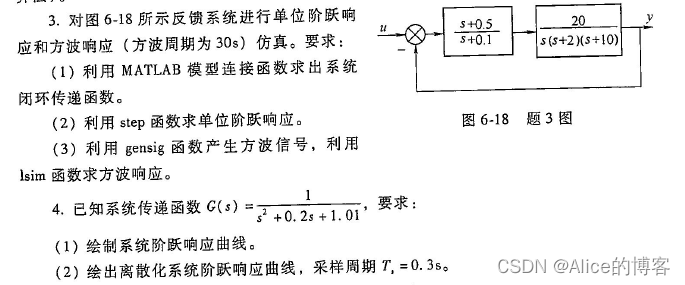
sys1 = tf(num,den);z = [];p = [0,-2,-10];k = 20;sys2 = zpk(z,p,k);sys3 = series(sys1,sys2);sys4 = feedback(sys3,1,-1);%习题6,第3题(2)subplot(1,2,1)step(sys4);%计算系统对单位阶跃输入的响应%习题6,第3题(3)[u,t] = gensig('square',30,60);subplot(1,2,2)lsim(sys4,'r',u,t);%计算系统对任意输入的响应

运行结果1：

>> sys4sys4 =20 (s+0.5)-------------------------------------------(s+10.23) (s+0.8195) (s^2 + 1.052s + 1.193)Continuous-time zero/pole/gain model.

运行结果2：

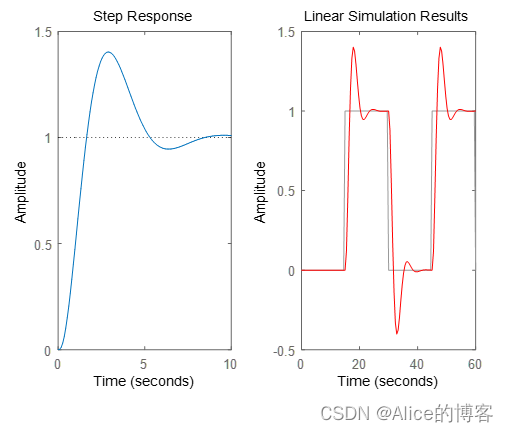
代码实现：

%习题6,第4题(1)
num = 1;
den = [1,0.2,1.01];
sys = tf(num,den);subplot(1,2,1)
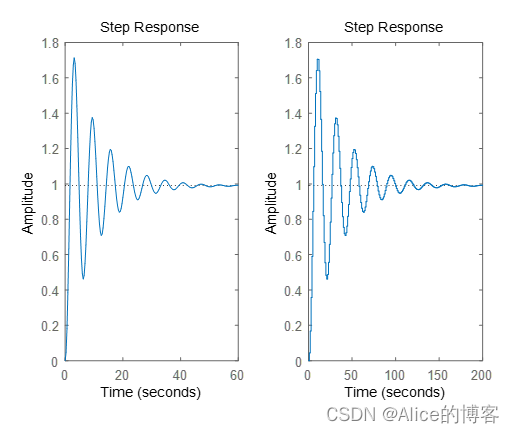
step(sys);%习题6,第4题(2)
sys1 = c2d(sys,0.3,'zoh');%传递函数离散
[num1,den1] = tfdata(sys1,'v');%离散后提取分子分母
subplot(1,2,2)
dstep(num1,den1);

运行结果：

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！