落谷3循环结构高精度阶乘和

高精度阶乘和

问题描述

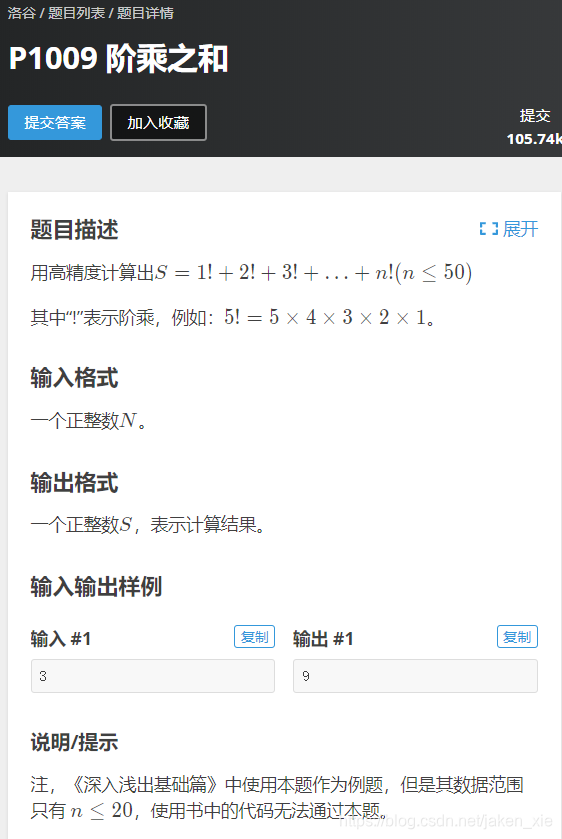
思路
首先明确本体的循环结构，也就是一需要一重循环，每次求完阶乘之后把结果加入到要输出的res数组里面即可，由于是高精度，所以可以构造两个函数分别求乘法和加法，，求n阶乘问题可以简化为n-1的阶乘在乘以n，所以每次乘法的结果都保存在一个数组中，下次利用此数组乘n即可求出n的阶乘，加法的结构保留在res中，每次求完阶乘就实行加法操作

代码
#include
#include
#include
using namespace std;

vector chengfa(vector &a,int n)//求高精度乘法的函数
{
int jinwei=0;//代表进位，乘法的进位可以很大
for(int i=0;i
a[i]=a[i]*n+jinwei;//我们数学中算乘法的步骤
jinwei=a[i]/10;
a[i]=a[i]%10;//取余获得a[i]
}
while (jinwei!=0) {//如果算到最后进位不为0，那就要实行以下操作
a.push_back(jinwei%10);//比如a储存的结果为2345，而此时的进位为12，我们就要实行操作将a变为234512，即在数组后添加12即可
jinwei/=10;
}
return a;
}
vector jiafa(vector & a,vector & b)//结果储存在a中
{
int jinwei=0;//同理加法也需要进位，，加法的进位小于10，不像乘法
if(a.size() for(int i=0;i
a.push_back(0);
}
}
for(int i=0;i a[i]=a[i]+b[i]+jinwei;
jinwei=a[i]/10;
a[i]%=10;
}
if(jinwei!=0) {
a.push_back(jinwei);
}
return a;
}
int main()
{
int n;
cin>>n;
vector res;
vector jiecheng;
res.push_back(1);
jiecheng.push_back(1);
for(int j=2;j<=n;j++) {//计算j的阶乘，只需在j-1阶乘的基础上再乘以j
jiecheng=chengfa(jiecheng,j);
res=jiafa(res,jiecheng);
}
for(int i=res.size()-1;i>=0;i–) {
cout< }
return 0;
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！