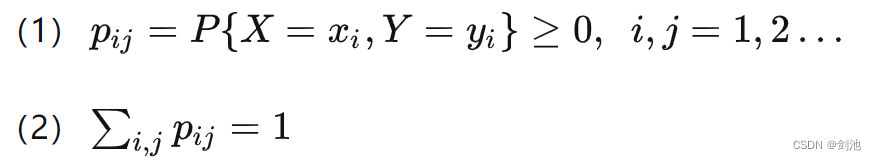AI 人工智能之概率论基础(2)
二维随机变量
设试验 E 的样本空间为 S={e} ,而 X=X(e) , Y=Y(e) 是定义在 S={e} 上的两个随机变量成为由这两个随机变量组成的向量 (X(e),Y(e)) 为二维随机变量或者二维随机向量。
设 (X,Y) 为二维随机变量,对任意实数 x,y ,二元函数:
![]()
称为二维随机变量 (X,Y) 的分布函数,或者称为随机变量 X 和 Y 的联合分布函数。
二维随机变量分布函数具有下列五条基本性质:

二维离散型随机变量
若二维随机变量 (X,Y) 的所有取值为有限对或者可列对 (xi,yj) , i,j=1,2,… ,则称 (X,Y) 是离散型随机变量。
记 P{X=xi,Y=yi}=pij, i,j=1,2,… ,则称它为二维离散型随机变量 (X,Y) 的(概率)分布律,或者称为 X 和 Y 的联合(概率)分布律。
分布律有两种常用的表示法:公式法和列表法。
这种分布律具有下面两种性质:

二维离散随机变量的联合分布
设(X,Y)是二维随机变量,x,y是任意实数,二元函数:
F(x,y)=P({X≤x∩Y≤y})=P(X≤x,Y≤y),被称二维随机变量(X,Y)的分布函数,或称为X和Y的联合分布函数。
将二维随机变量(X,Y)看成是平面上随机点的坐标,分布函数F(x,y)在(x,y)处的函数值就是随机点(X,Y)落在如图以(x,y)为顶点而位于该点左下方的无穷矩形区域内的概率。
例如:设随机变量X在1,2,3,4四个整数中等可能地取一个值,另一个随机变量在中等可能地取一整数值。试求的分布律。
解:P(X = i) = 1/4, i = 1,2,3,4
| X | Y | P |
|---|---|---|
| X=1 | Y:1 | P(Y=j|x=1) = 1 |
| X=2 | Y:1,2 | P(Y=j|x=2) = 1/2 |
| X=3 | Y:1,2,3 | P(Y=j|x=13) = 1/3 |
| X=4 | Y:1,2,3,4 | P(Y=j|x=4) = 1/4 |
根据联合分布率:P(AB)=P(A)·P(B|A)(乘法公式):
P(XY) = P(X=i) · P(Y=j|x=i) = 1
| 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1 | ||||
| 2 | 0 | |||
| 3 | 0 | 0 | ||
| 4 | 0 | 0 | 0 |
联合分布函数
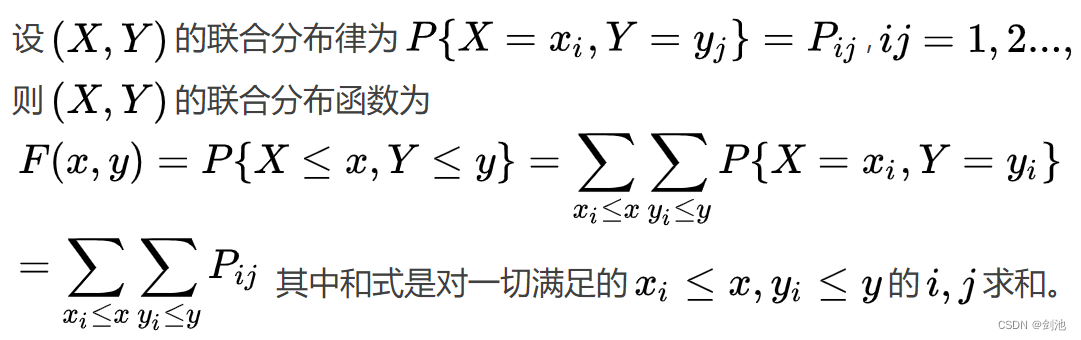
二维连续性随机变量
对二维随机变量(X,Y)的分布函数F(x,y),如果存在非负函数f(x,y),使得对任意x,y有:
则称(X,Y)是二维连续型随机变量,称f(x,y)为(X,Y)的联合概率密度,记为(X,Y) ~ f(x,y) .
f(x,y) 的性质(二元函数f(x,y)是二维连续型随机变量的概率密度的充要条件):
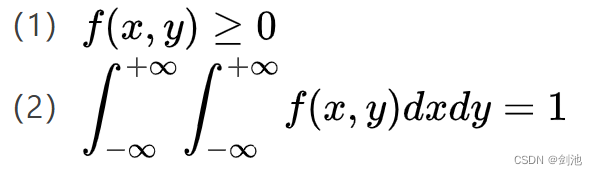
联合分布函数、联合概率密度函数性质:
设(X,Y)的联合分布函数为F(x,y),概率密度为f(x,y),则:
(1) F(x,y) 是(x,y)的二元连续函数;
(2) 在的连续点处,有
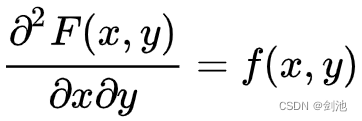

(4)设G是平面上的某个区域,则
![]()
[注]这是计算概率,及求随机变量函数的分布的依据.
例如:

边缘分布
边缘分布函数:二维随机变量的 X 和 Y 都是随机变量,有各自的分布函数,记为 ,称为边缘分布函数:
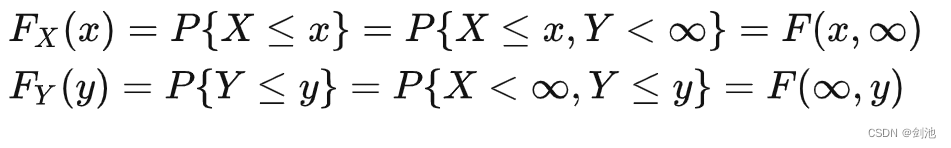
二维离散型随机变量的边缘分布函数:
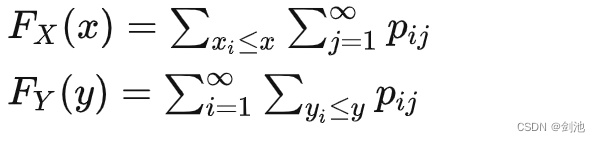
二维离散型随机变量的边缘分布率:
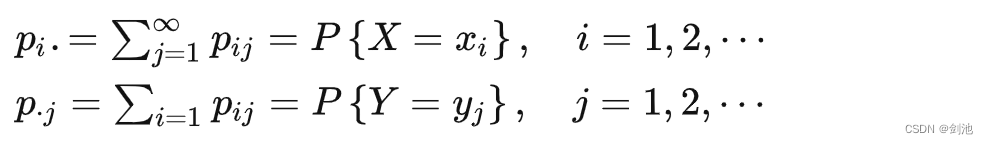
多维随机变量的边缘分布
多维随机向量 (X1,X2,...,Xn) 的联合分布函数为 F(x1,x2,⋯,xn)
1 维边缘分布函数:比如关于 的 1 维边缘分布函数
2 维边缘分布函数:比如关于 的 2 维边缘分布函数
依次,多维随机变量可以有 k, (1≤k 离散型随机变量有 k 维边缘分布律,这里以 k=1 为例: 连续性边缘分布概率密度 连续型随机变量有 k 维边缘概率密度,这里以 k=1 为例: ![]()
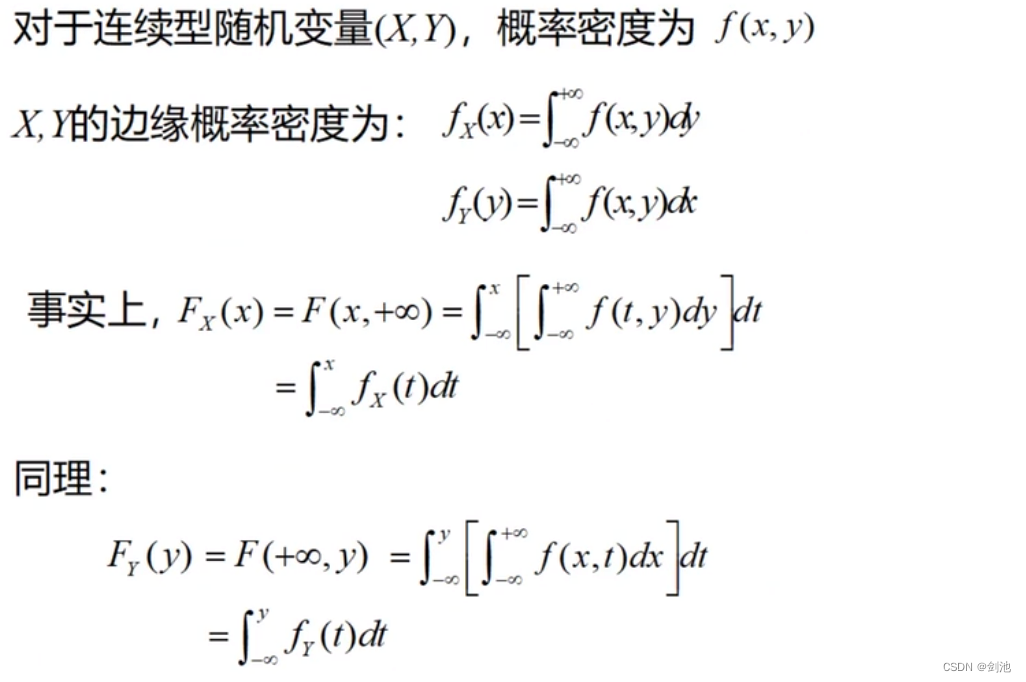
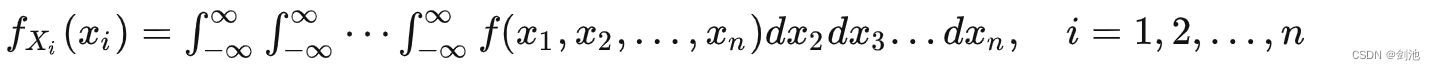
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!