离散（图论）

一、图的基本概念：

握手定理：在任何无向图中，所有顶点的度数之和等于边数的2倍；

                  在任何有向图中，所有顶点的度数之和等于边的2倍，所有顶点的入度之和等于出度之和等于边的条数；

        简单图：在图中，若不存在顶点到其自身的边，且同一条边不重复出现，则称这样的图为简单图

         无向完全图：在无向图中，如果任意两个顶点之间都存在边，则称该图为 无向完全图

顶点度数 = 点数 - 1

        有向完全图：在无向图中，如果任意两个顶点之间都存在边，则称该图为 无向完全图

顶点入度 = 顶点出度 = 点数 - 1；

        割点：在图中删去该点，则图不连通

        割边（桥）：在图中删去改边，则图不连通

        点连通度k(G) = 使连通图G成为一个不连通图需要删除的点的最小数目，记为K，则图也可称作K-连通图

       边连通度 = 使连通图G成为一个不连通图需要删除的点的最小数目，记为K，则图也可称作K-连通图

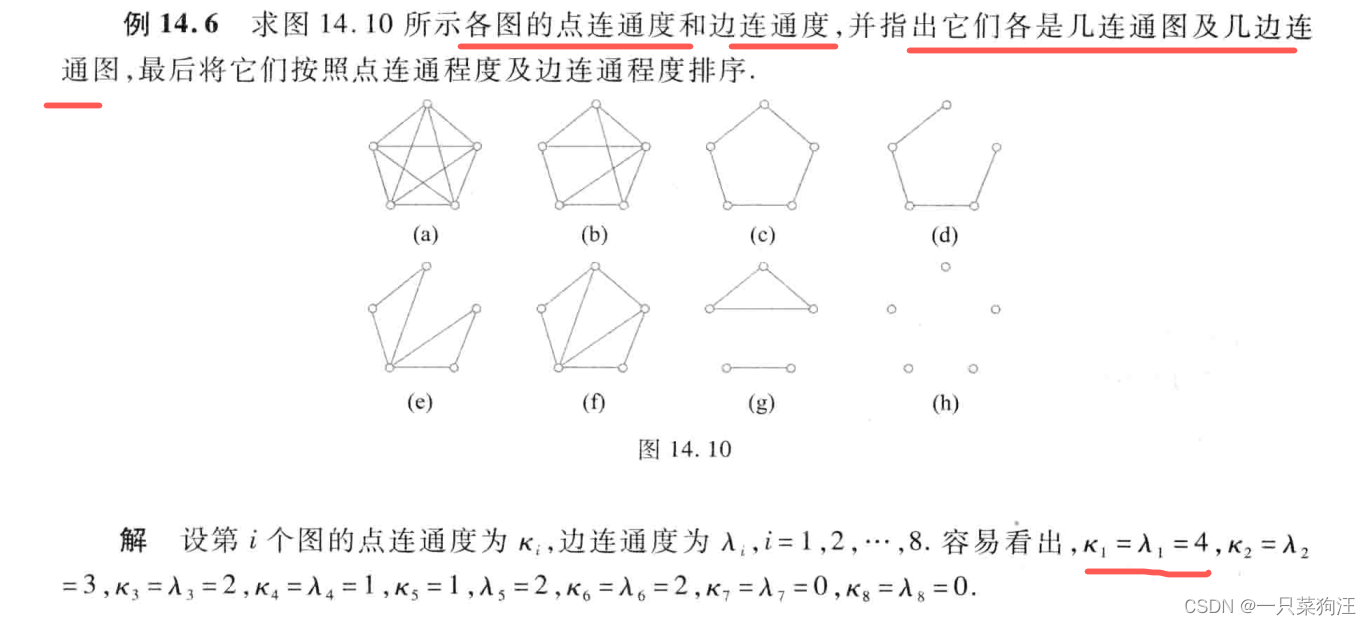
         （a）: 删除任何一个点的四条边，图都无法联通，故边连通度为4，删除任意四个点图都无法联通，故点连通度为4

        点割集：割点 + 去除n个点图无法联通且集合之间不能重复出现元素

        边割集：同上

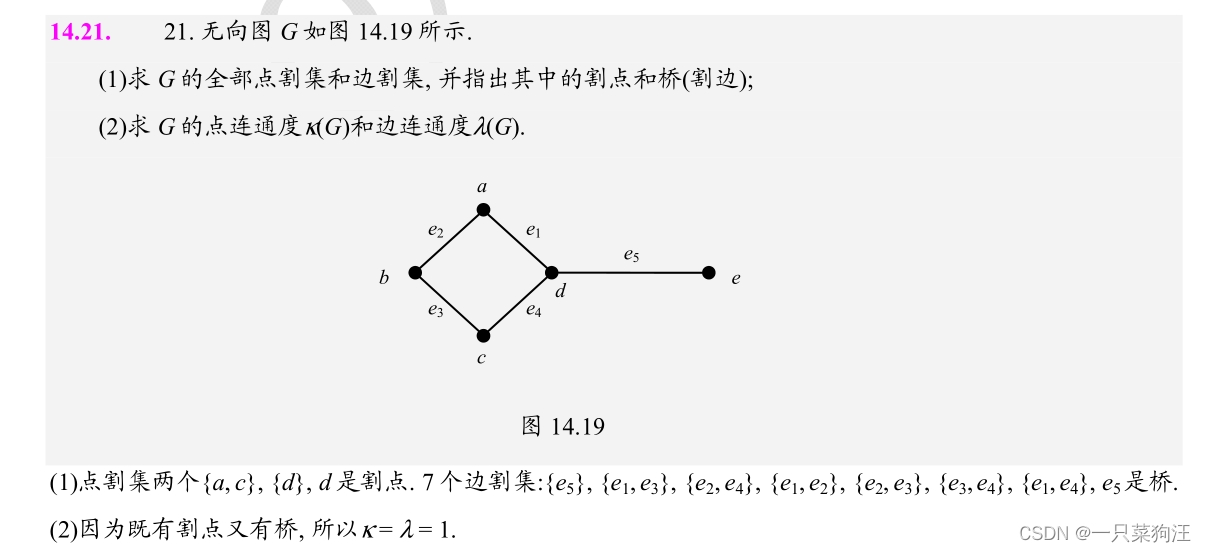
         无向图的关联矩阵：

        行表示边，列表示点，用关联矩阵画图时可根据列中有1的相连，例：e2时 v1和v2相连，若为2，则说明为环 

        有向图的关联矩阵：

         若为1则为出，-1为进，画图原理同上

        邻接矩阵：a(ij)表示从vi到vj的边数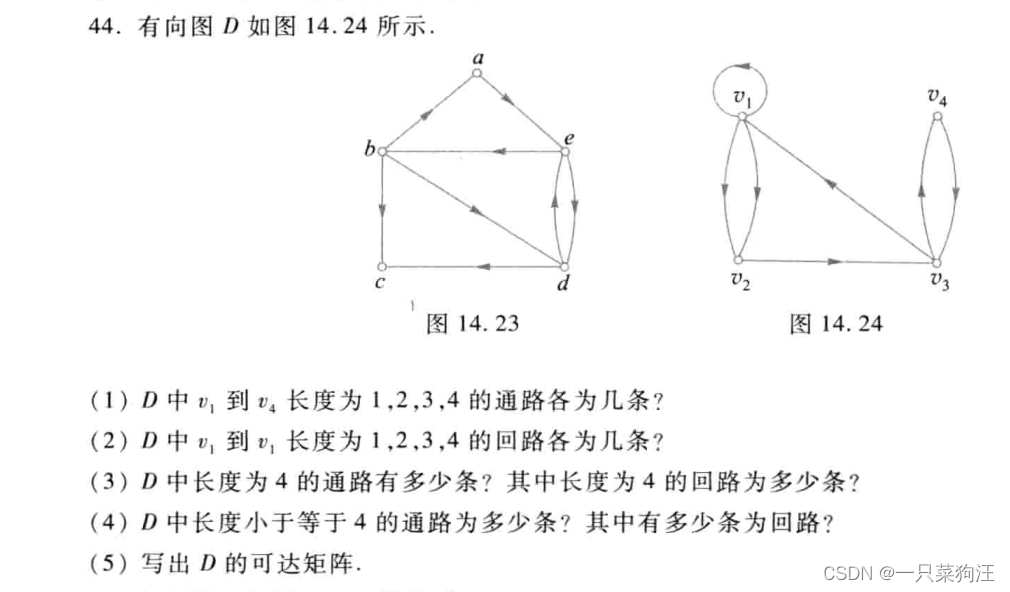

         1) v1到v4为a(1,4)的数目   2）v1到v1为a（1,1）的数目

             回路的数目为从左上到 右下的和，例3） = 5+2+3+1 = 11

             通路的数目整个邻接矩阵都是，加起来即可，A的n次方代表长度为n的通路或回路

二、欧拉图与哈密顿图

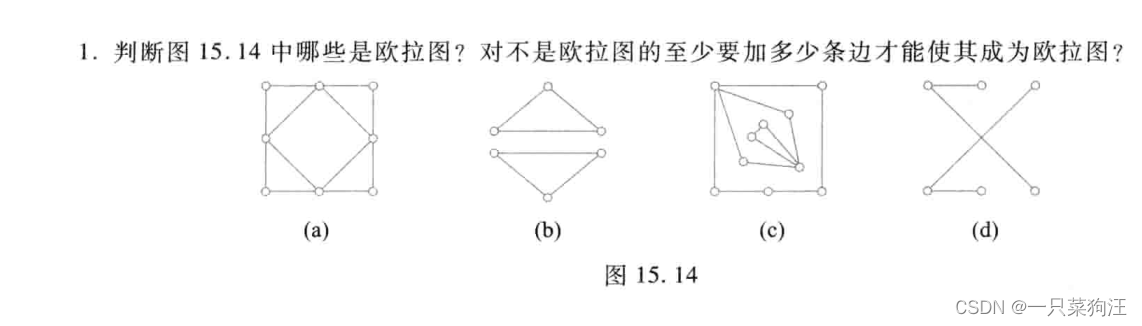
                有上述定理可知：a中结点度数均为偶数故为欧拉图，b不连图不是，c是，d存在奇数度数

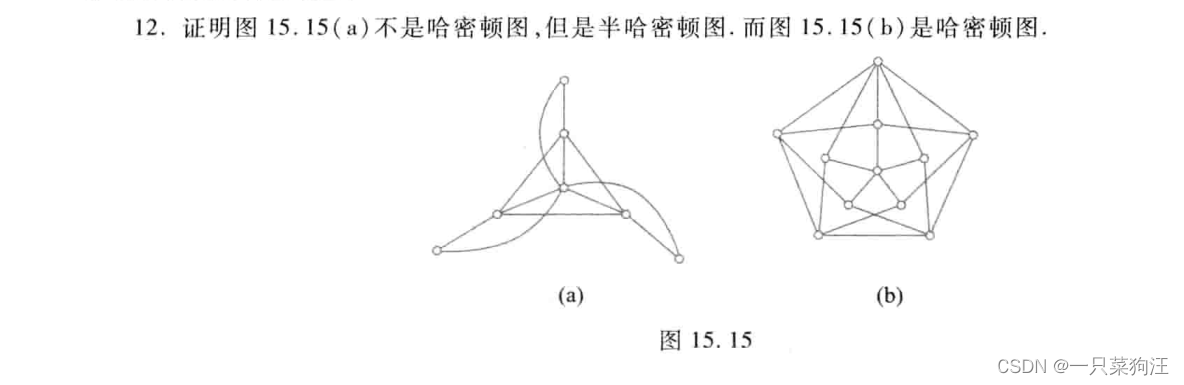
         水平有限没整理好

        最短路：

求从v1到其余各点的最短路径和距离

Dijkstra标号法求解：从局部最优推至全局最优 

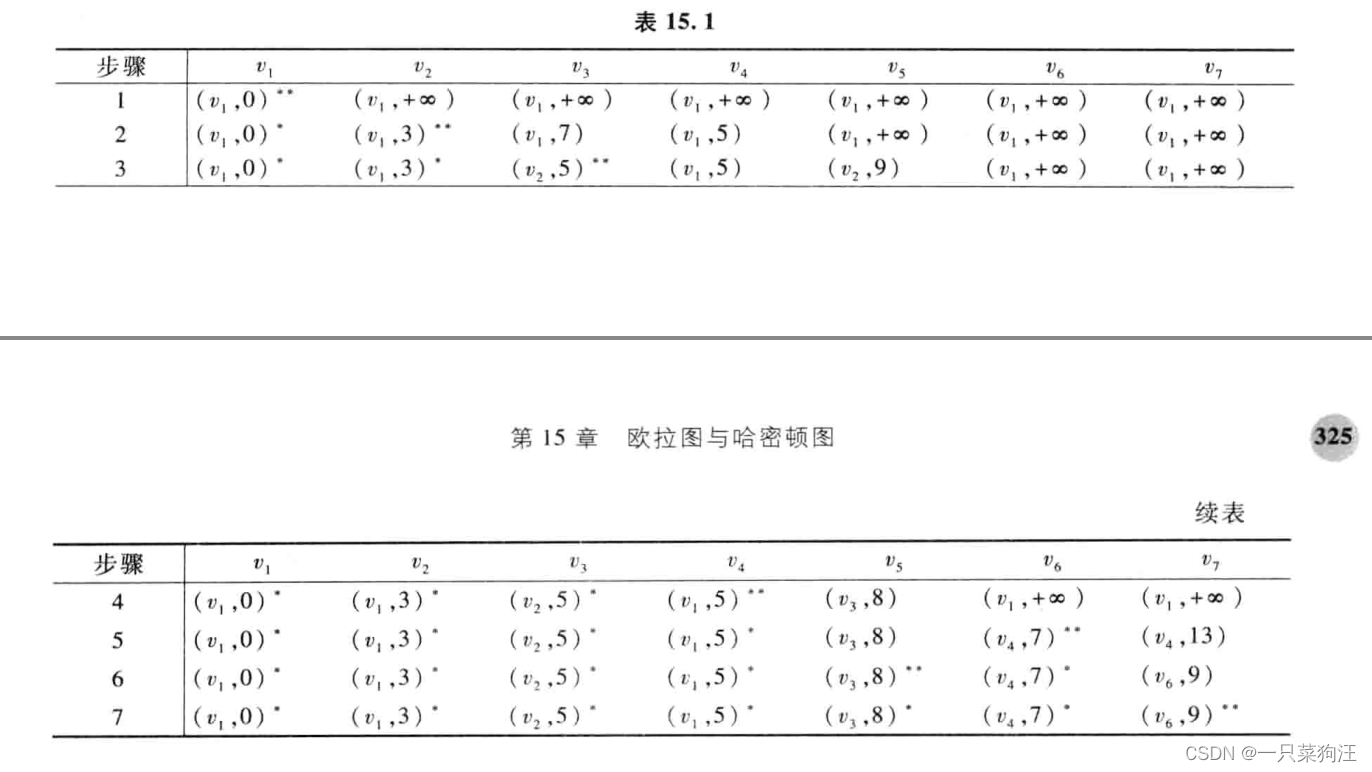
三、树

        2. 有握手定理 与 m = n -1联立求解即可 m为边，n为节点

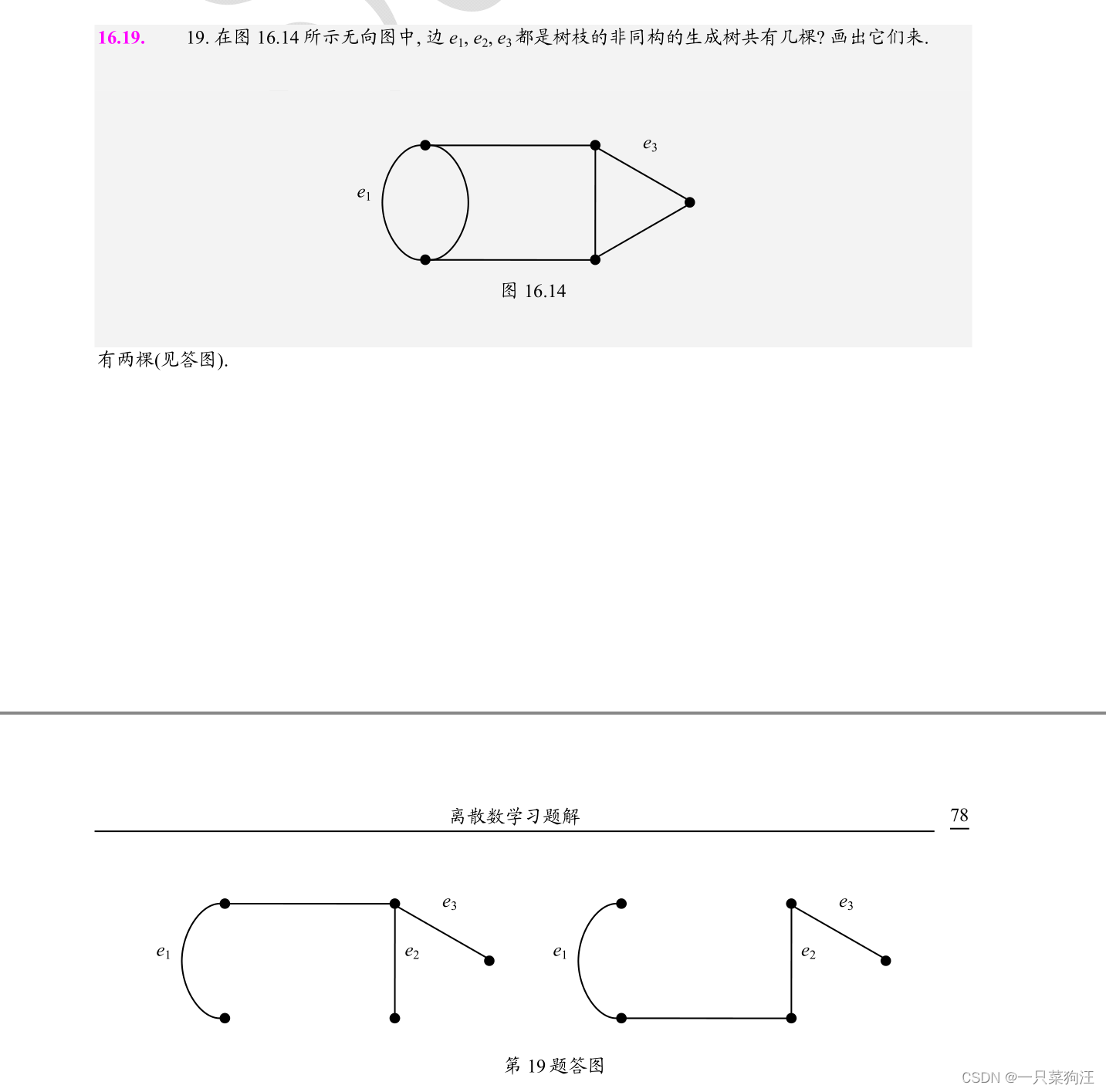
 破圈法求解： 

按照每条边的原位置建，不要出现圈即可

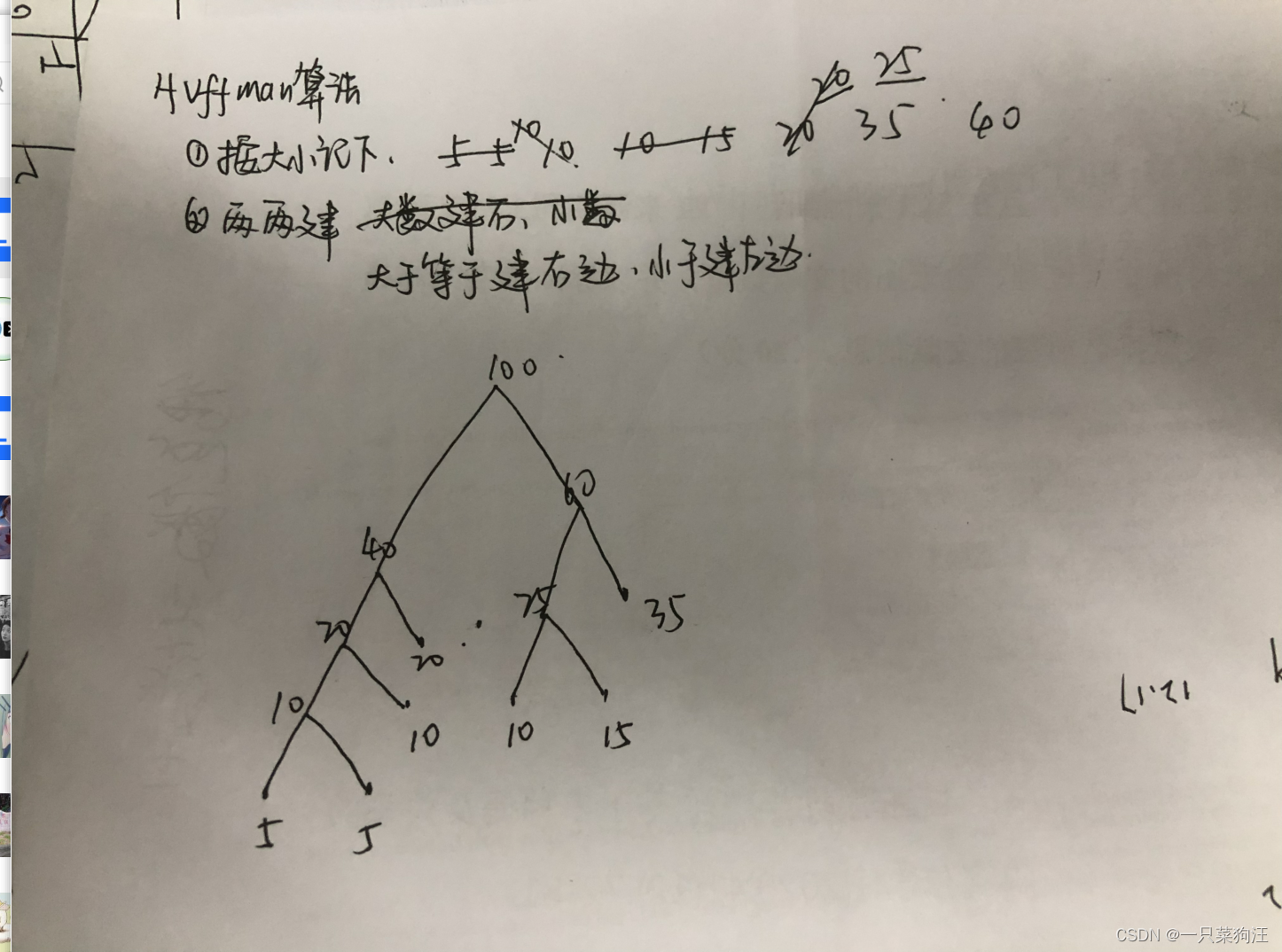
         左边的边为0 ， 右边的边为1，从头写到叶节点即为最佳前缀编码

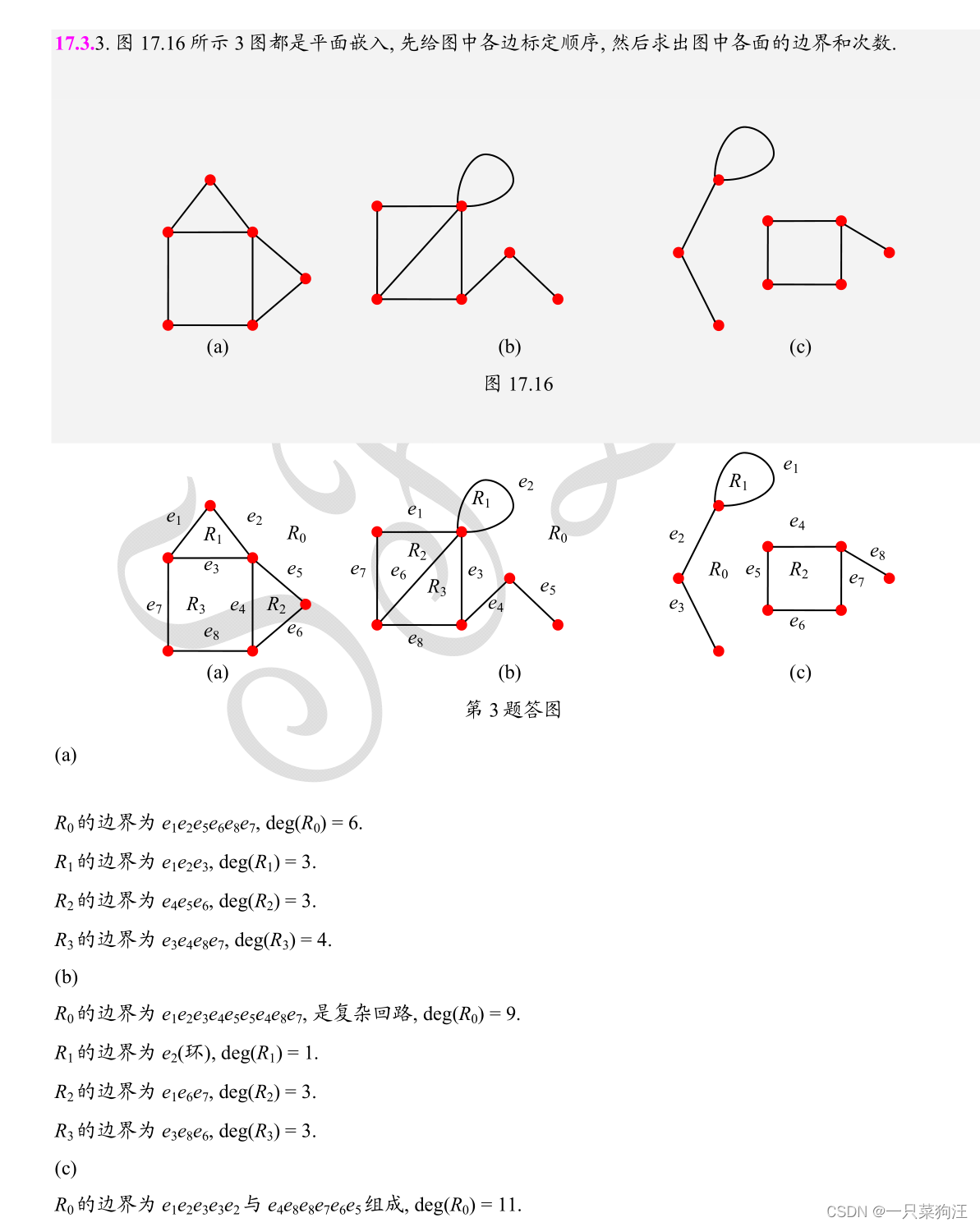
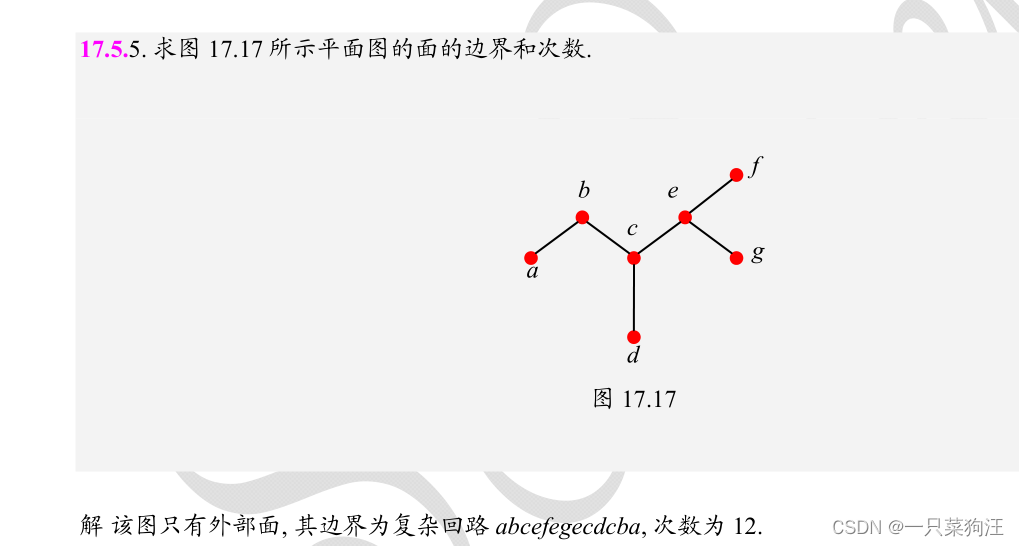
四、平面图

         平行边与环不影响图的平面性

        平面图所有面的次数之和等于边数的两倍 

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！