拼多多 2020校园招聘 骰子期望（古典概型，互斥）

扔n个骰子，第i个骰子有可能投掷出Xi种等概率的不同的结果，数字从1到Xi。所有骰子的结果的最大值将作为最终结果。求最终结果的期望。

解题思路：

这里我们需要用古典概型计算每一个取值的概率，然后再算期望。

我们知道，总共的可能性是：Xi的连乘。我举个简单的例子

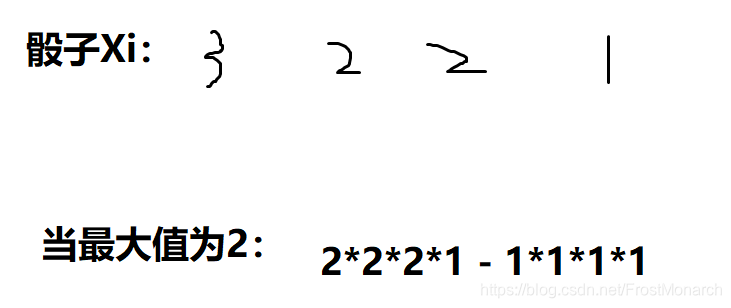
2*2*2*1代表我们每一个骰子大于等于2的我们都认为可以取[1,2]两种可能，至于有1个1，他只有[1,1]种可能。最后为什么需要减呢，因为有可能上面枚举的情况中出现大家出现值都小于2的情况，所以减去[1,1,1,1]这种可能性。

#include 
using namespace std;
int main(){int n;cin>>n;vector arrmv;int maxele = -1e9;for(int i=0;i>t;maxele = max(maxele,t);arrmv.push_back((double)t);}double fenmu=1;for(int i=0;i<(int)arrmv.size();i++)fenmu*=arrmv[i];double ans=0;for(int i=1;i<=maxele;i++){double tmp=1;for(int j=0;j<(int)arrmv.size();j++)tmp*=min((double)i,arrmv[j]);double tmp2=1;for(int j=0;j<(int)arrmv.size();j++)if(arrmv[j]>=i)tmp2*=i-1;else tmp2*=arrmv[j];// cerr<

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！