Alvarze方法(1976)原文译文

Energy-selective Reconstructions in X-ray Computerized Tomography.

希望对大家有所帮助，不准确之处烦请谅解。

---

1. Introduction

提出了两步提取完全能量相关信息的理论

• 首先，本文描述了用少量与能量无关的常数来表示每一能量下的完整的赋值系数函数的方法。这些常数指定了占总线性衰减系数的光电和康普顿散射相互作用的数量
• 接下来，它将显示计算机断层摄影技术可用于计算这些常数在一个物体的横截面内的每一点。诊断信息可以直接从这些常量中得到，或者它们可以被用来在诊断范围内的任何能量下提供线性衰减系数的重建.

讨论了能量相关信息在诊断中的应用，基本上可以推断出两种信息

• 光电系数很大程度上依赖于原子序数，并且表示了该物体的组成
• 康普顿散射效率取决于电子密度，而电子密度反过来又与大多数材料的质量密度成正比

本文

• 考虑了噪音和病人剂量的影响
• 推导了由计数噪声引起的误差的一般表达式
• 对典型系统的这些表达式进行了评估
• 讨论了散射和有限探测器分辨率的影响

---

2. Representation of attenuation coefficients

f i f_i fi​是一组基函数， a i a_i ai​是一组常数，那么衰减系数$u(E)$可以表示为基函数的线性衰减系数的组合
u ( E ) = a 1 f 1 ( E ) + a 2 f 2 ( E ) + ⋯ + a 1 f 1 ( E ) (1) u(E) = a_1f_1(E) + a_2f_2(E) + \cdots + a_1f_1(E) \tag{1} u(E)=a1​f1​(E)+a2​f2​(E)+⋯+a1​f1​(E)(1)

基函数的最终选择是经验的，最终实验结果为：
u ( E ) = a 1 1 E 3 + a 2 f K N ( E ) (2) u(E) = a_1\frac{1}{E^3} + a_2f_{KN}(E) \tag{2} u(E)=a1​E31​+a2​fKN​(E)(2)
其中 f K N ( E ) f_{KN}(E) fKN​(E)是Klein-Nishina函数
f K N ( α ) = 1 + α α 2 [ 2 ( 1 + α ) 1 + 2 α − 1 α l n ( 1 + 2 α ) ] + 1 2 α l n ( 1 + 2 α ) − ( 1 + 3 α ) ( 1 + 2 α ) 2 (3) f_{KN}(\alpha) = \frac{1+\alpha}{\alpha^2} [\frac{2(1+\alpha)}{1+2\alpha} - \frac{1}{\alpha}ln(1+2\alpha)] + \frac{1}{2\alpha}ln(1+2\alpha) - \frac{(1+3\alpha)}{(1+2\alpha)^2} \tag{3} fKN​(α)=α21+α​[1+2α2(1+α)​−α1​ln(1+2α)]+2α1​ln(1+2α)−(1+2α)2(1+3α)​(3)

其中$\alpha =E/510.975keV$两种基函数具有物理意义， 1 E 3 \frac{1}{E^3} E31​近似于光电相互作用的能量依赖性， f K N ( E ) f_{KN}(E) fKN​(E)给出了康普顿散射总截面的能量依赖性

a 1 a_1 a1​和 a 2 a_2 a2​对物理参数的依赖性如下：
a 1 ≈ K 1 ρ A Z n , n ≈ 4 (4) a_1 \approx K_1\frac{\rho}{A}Z^{n}, \quad n \approx 4 \tag{4} a1​≈K1​Aρ​Zn,n≈4(4)
a 2 ≈ K 2 ρ A Z (5) \qquad a_2 \approx K_2\frac{\rho}{A}Z \tag{5} a2​≈K2​Aρ​Z(5)
其中 K 1 K_1 K1​和 K 2 K_2 K2​是常数，$\rho$是质量密度，$A$是原子质量，$Z$是原子序数

这些函数在表示衰减系数函数时的用处是众所周知的(Hale 1974)。最近，对人体材料衰减系数的高精度测量已经成为可能(Rao and Gregg 1973; Phelps, Hoffman and Ter-Pobronogan 1975)

用最小二乘曲线拟合方法对这些数据进行了拟合，结果良好.在30- 200kev范围内，计算值与实验值的最大差异小于1%，平均误差为0.1%

---

3. Incorporation of energy spectral measurements into computerized tomography

在计算机断层摄影术中，测量我们所重建的函数的线积分。X射线系统从根本上测量线性衰减系数的线积分，即$\int \mu (x,y;E)ds$等价于测量系数 a 1 a_1 a1​和 a 2 a_2 a2​的线积分
由于
u ( x , y ; E ) = a 1 ( x , y ) 1 E 3 + a 2 ( x , y ) f K N ( E ) (6) u(x, y; E) = a_1(x, y)\frac{1}{E^3} + a_2(x, y)f_{KN}(E) \tag{6} u(x,y;E)=a1​(x,y)E31​+a2​(x,y)fKN​(E)(6)
有
∫ u ( x , y ; E ) d s = A 1 1 E 3 + A 2 f K N ( E ) (7) \int u(x, y; E)ds = A_1\frac{1}{E^3} + A_2f_{KN}(E) \tag{7} ∫u(x,y;E)ds=A1​E31​+A2​fKN​(E)(7)
其中 A 1 = ∫ a 1 ( x , y ) d s , A 2 = ∫ a 2 ( x , y ) d s (8) A_1 = \int a_1(x,y)ds, A_2 = \int a_2(x,y)ds \tag{8} A1​=∫a1​(x,y)ds,A2​=∫a2​(x,y)ds(8)

构造 a 1 ( x , y ) a_1(x, y) a1​(x,y)和 a 2 ( x , y ) a_2(x, y) a2​(x,y)需要在物体投影的每一点上测量线积分 A 1 A_1 A1​和 A 2 A_2 A2​这意味着每个点都必须有两个独立的信息。这可以通过用两个不同的源光谱进行强度测量来获得
I 1 ( A 1 , A 2 ) = T ∫ S 1 ( E ) e − A 1 / E 3 − A 2 f K N ( E ) d E (9) I_1(A_1, A_2) = T\int S_1(E)e^{-A_1/E^3-A_2f_{KN}(E)} dE \tag{9} I1​(A1​,A2​)=T∫S1​(E)e−A1​/E3−A2​fKN​(E)dE(9)
I 2 ( A 1 , A 2 ) = T ∫ S 2 ( E ) e − A 1 / E 3 − A 2 f K N ( E ) d E (10) I_2(A_1, A_2) = T\int S_2(E)e^{-A_1/E^3-A_2f_{KN}(E)} dE \tag{10} I2​(A1​,A2​)=T∫S2​(E)e−A1​/E3−A2​fKN​(E)dE(10)
其中$T$是总共的测量时间
方程中 S 1 S_1 S1​和 S 2 S_2 S2​是 I 1 I_1 I1​和 I 2 I_2 I2​总计数的能谱光子数，或者 S 1 S_1 S1​和 S 2 S_2 S2​是 I 1 I_1 I1​和 I 2 I_2 I2​合计能量的能谱。本文考虑光子数谱的情况，计算能量的能谱可以得到类似的结果

光谱 S 1 S_1 S1​和 S 2 S_2 S2​可以以多种方式形成。它们可以由两种不同的同位素源通过单能辐射产生。可以通过交替穿过两种转换材料 g 1 ( E ) g_1(E) g1​(E)和 g 2 ( E ) g_2(E) g2​(E)对单一源光谱进行滤波而获得，即 S 1 = S ( E ) g 1 ( E ) S_1 = S(E)g_1(E) S1​=S(E)g1​(E)， S 2 = S ( E ) g 2 ( E ) S_2 = S(E)g_2(E) S2​=S(E)g2​(E)

在计数检测器系统中，可以进行单电平脉冲高度分析，其中 I 1 I_1 I1​表示从0到某个阈值能量 E T E_T ET​的计数， I 2 I_2 I2​表示 E T E_T ET​以上的计数。对于半导体探测器来说，这是一个很好的模型，但是对于低分辨率的探测器来说过于理想化。探测器响应函数将是理想矩形响应函数与探测器能量分辨率响应的卷积。由于与能量相关的信息相对简单，所需要的就是探测器将光子分成两个不同的能量组。因此，相对低分辨率的探测器就足以提取信息。

无论采用何种格式，只要Jacobi矩阵
J = d e t ( ∂ I 1 ∂ A 1 ∂ I 1 ∂ A 2 ∂ I 2 ∂ A 1 ∂ I 2 ∂ A 2 ) (11) J = det \begin{pmatrix} \frac{\partial I_1}{\partial A_1} & \frac{\partial I_1}{\partial A_2} \\ \frac{\partial I_2}{\partial A_1} & \frac{\partial I_2}{\partial A_2} \end{pmatrix} \tag{11} J=det(∂A1​∂I1​​∂A1​∂I2​​​∂A2​∂I1​​∂A2​∂I2​​​)(11)
非零，那么就可以通过{eq9}和{eq10}计算得到 A 1 A_1 A1​和 A 2 A_2 A2​。当所有的线积分集合 A 1 A_1 A1​和 A 2 A_2 A2​已知时，可以利用传统方法重建 a 1 ( x , y ) a_1(x, y) a1​(x,y)和 a 2 ( x , y ) a_2(x, y) a2​(x,y)

散射可能是一个严重的实际考虑，取决于扫描系统的几何形状。由于{eq9}和{eq10}的非线性性质，很难预测添加一个相对恒定的散射项的影响。传统的光强系统也会受到散射的影响。他们通过对测量值取对数来进行非线性处理，过度的散射会导致重建过程中出现伪影(Stonestrom and Macovski 1975)。这些系统的成功运行表明，通过使用适当的准直器，散射可以降低到可以忽略的水平

---

4. Simulation of computerized tomography system with energy spectral measurements

一种计算机模拟用以显示如何在计算机层析成像系统中使用能谱技术。使用了如图l所示的测试对象。它包括一个充满全脑型组织的骨环，中心的病灶由脂肪型组织组成。实验测量的衰减系数用于骨(ICRU 1970)和组织(Phelps et al. 1975)。大脑和脂肪的$ a_1 $和$ a_2 $的值分别为:
b r a i n : a 1 = 4792 k e V 3 c m − 1 , a 2 = 0.1694 c m − 1 f a t : a 1 = 2868 k e V 3 c m − 1 , a 2 = 0.1784 c m − 1 brain: \quad a_1 = 4792keV^3 cm^{-1}, \quad a_2 = 0.1694cm^{-1} \\ fat: \quad a_1 = 2868keV^3 cm^{-1}, \quad a_2 = 0.1784cm^{-1} brain:a1​=4792keV3cm−1,a2​=0.1694cm−1fat:a1​=2868keV3cm−1,a2​=0.1784cm−1
假设一个理想的脉冲高度分析测量。图2是测量得到的105kVp X射线管光谱(Epp and Weiss 1966)，对160个投影计算了在59千伏以下和以上的透射光谱中的计数数。这是重建方案中使用的原始数据。散射是被忽视的。对这160个投影，需要求解积分{eq9}和{eq10}。由于 S 1 S_1 S1​和 S 2 S_2 S2​未知，所以不可能求得解析解。取而代之的是，下面的技巧被用来解这些方程。引入了具有待定系数的{eq9}和{eq10}的一般形式。这些系数是通过测量已知 A 1 A_1 A1​和 A 2 A_2 A2​材料的透射率，然后用最小二乘曲线拟合的方法，通过实验确定的。对于 A 1 A_1 A1​和 A 2 A_2 A2​的感兴趣取值范围，可以使用幂级数形式：
l n I 1 = b 0 + b 1 A 1 + b 2 A 2 + b 3 A 1 2 + b 4 A 2 2 + b 5 A 1 A 2 + b 6 A 1 3 + b 7 A 2 3 (12) lnI_1 = b_0 + b_1A_1 + b_2A_2 + b_3A_1^2 + b_4A_2^2 + b_5A_1A_2 + b_6A_1^3 + b_7A_2^3 \tag{12} lnI1​=b0​+b1​A1​+b2​A2​+b3​A12​+b4​A22​+b5​A1​A2​+b6​A13​+b7​A23​(12)
l n I 2 = c 0 + c 1 A 1 + c 2 A 2 + c 3 A 1 2 + c 4 A 2 2 + c 5 A 1 A 2 + c 6 A 1 3 + c 7 A 2 3 (13) lnI_2 = c_0 + c_1A_1 + c_2A_2 + c_3A_1^2 + c_4A_2^2 + c_5A_1A_2 + c_6A_1^3 + c_7A_2^3 \tag{13} lnI2​=c0​+c1​A1​+c2​A2​+c3​A12​+c4​A22​+c5​A1​A2​+c6​A13​+c7​A23​(13)
一旦确定了系数组 b i {b_i} bi​和 c i {c_i} ci​，{eq12}和{eq13}就成为两个联立的三次方程，可以用推广的Newton-Raphson方法数值求解(McCracken and Dorn 1964)

{eq12}和{eq13}的精度可以证明如下：系数 b i {b_i} bi​和 c i {c_i} ci​是通过计算不同 A 1 A_1 A1​和 A 2 A_2 A2​的 I 1 I_1 I1​和 I 2 I_2 I2​来确定的。然后对任意已知的 A 1 A_1 A1​和 A 2 A_2 A2​计算积分 I 1 I_1 I1​和 I 2 I_2 I2​。通过求解{eq12}和{eq13}得到 A 1 A_1 A1​和 A 2 A_2 A2​的估计值。估计值与实际值的比较如表1所示。

进行了三次重建。如图1所示：

1. 传统的重建方法是对传输光子总数的对数
2. 重建的 a 1 a_1 a1​是光电效应部分
3. 重建的 a 2 a_2 a2​是康普顿散射部分

选择颅骨中心病变的密度，使透射谱平均能量为63 keV，衰减系数与周围组织相等。因此，在只使用光强重建结果中，它几乎是看不见的。由于它在其他能量下的衰减系数与周围组织的衰减系数不同，因此在康普顿和光电重建中比较明显。一种简单的卷积重建算法(Bracewell and Riddle 1967)被用于解释由物体不连续性造成的相对较大的伪影。如表1所示，线积分本身的精度在百分之零点几以内。

在强度重建中，邻近头骨的软组织区域也有一个大的杯状突起。这是一个光谱变换伪影(Macovski, Alvarez, Chan and Stonestrom 1975)，它是由于靠近头骨边缘的光束硬化而引起的。硬化导致平均能量的转移，这取决于路径中材料的数量，这是{eq12}和{eq13}非线性性质的物理基础。能谱分析为校正这一重要伪影提供了一种全面准确的技术。仅限强度的系统必须使用水容器(McCullough, Baker, Houser and Reese 1974)和计算技术来进行伪影校正。

---

5. Noise and patient dose considerations

与其他X射线系统一样， A 1 A_1 A1​和 A 2 A_2 A2​的测量精度受到患者剂量考虑的限制。由于确定线积分需要同时求解两个方程，误差的计算比较复杂。假设泊松计数噪声是限制因素，计算测量数据标准偏差的程序在附录中显示。 A 1 A_1 A1​和 A 2 A_2 A2​标准差的结果为：
σ A 1 = [ ( m 12 2 / I 2 ) + ( m 22 2 / I 1 ) ] 1 2 m 11 m 22 − m 12 m 21 (14) \sigma_{A_1} = \frac{[(m_{12}^2/I_2) + (m_{22}^2/I_1)]^{\frac{1}{2}}}{m_{11}m_{22} - m_{12}m_{21}} \tag{14} σA1​​=m11​m22​−m12​m21​[(m122​/I2​)+(m222​/I1​)]21​​(14)
σ A 2 = [ ( m 11 2 / I 2 ) + ( m 21 2 / I 1 ) ] 1 2 m 11 m 22 − m 12 m 21 (15) \sigma_{A_2} = \frac{[(m_{11}^2/I_2) + (m_{21}^2/I_1)]^{\frac{1}{2}}}{m_{11}m_{22} - m_{12}m_{21}} \tag{15} σA2​​=m11​m22​−m12​m21​[(m112​/I2​)+(m212​/I1​)]21​​(15)
其中在这些表达式中， I 1 I_1 I1​和 I 2 I_2 I2​是第3节所讨论的测量1和2中的计数数，并且有：
m 11 = ∂ ln ⁡ I 1 ∂ A 1 , m 12 = ∂ ln ⁡ I 1 ∂ A 2 (16) m_{11} = \frac{\partial \ln I_1}{\partial A_1}, \qquad m_{12} = \frac{\partial \ln I_1}{\partial A_2} \tag{16} m11​=∂A1​∂lnI1​​,m12​=∂A2​∂lnI1​​(16)
m 21 = ∂ ln ⁡ I 2 ∂ A 1 , m 22 = ∂ ln ⁡ I 2 ∂ A 2 (17) m_{21} = \frac{\partial \ln I_2}{\partial A_1}, \qquad m_{22} = \frac{\partial \ln I_2}{\partial A_2} \tag{17} m21​=∂A1​∂lnI2​​,m22​=∂A2​∂lnI2​​(17)

这些方程式的物理解释很有趣。这两个表达式的分母本质上都是行列式，通过与线性方程组的类比，决定了{eq9}和{eq10}的条件。一个小的行列式意味着一个病态的方程组，因此在确定 A 1 A_1 A1​和 A 2 A_2 A2​时存在很大的误差。表达式的分子随着计数的增加而变小。显然，一个条件病态的系统需要更多的光子才能达到与条件较好的系统相同的精度。可以通过改变滤波器函数 g 1 ( E ) g_1(E) g1​(E)和 g 2 ( E ) g_2(E) g2​(E)来调节。我们正在研究最优滤波函数的选择问题。

剂量的计算是一个复杂的问题。为了获得剂量的粗略估计，可以假设一个典型的头部扫描仪的配置。以脉冲高度分析计数探测器为例，误差主要由阈值能量和体厚决定。使用图2所示的能谱，入射光子总数为 5 × 7 10 5×7^{10} 5×710，入射谱的平均能量大约为50keV。因此，假设所有的光子都停止在体内，能量沉积将约为4尔格。假设能量在辐照体积(直径18cm，厚度1.3cm的圆柱体)内均匀分布，在180度角的160个位置测量，剂量为3-5拉德，这与常规扫描的剂量相当。

由计数噪声引起的误差如图3所示。它们被绘制成不同的阈能和体厚度。注意，光电线积分的误差大大高于康普顿线积分的误差。这是意料之中的，因为光电积分主要是由低能量的光子决定的，这些光子在体内更容易发生衰减。

---

6. Utilization of energy spectral information for diagnosis

在目前使用的计算机层析成像系统中，**用除去伪影的合成图像代表平均衰减系数。这种类型的一维表现的诊断能力是有限的。例如，病变表现为平均衰减系数增加，可能是钙化或密度增加的结果。**图4显示了利用所提出系统生成的数据类型。这表示in vitro（体外）样本(Phelps etal. 1975)。很明显，传统的沿轴线的投影几乎平行于横轴的投影的展示方式无法描绘出许多结构。我们正在开始一项获得in vivo（体内）数据的实验计划。

钙化的轮廓是一个重要的诊断参数的例子，如果给予足够的量化，将允许计算机断层扫描扩展到新的领域。许多乳腺癌的诊断依赖于具有很高空间分辨率的乳房x线照片，以观察许多恶性病变中微小的钙化。计算机层析成像的空间分辨率相对较差，因此钙化程度必须在较大的体积元上平均。对钙化的密度和程度进行准确的测量是很重要的，因为决定诊断的是这些参数而不是空间分布。

–推导这些估计数的方差表达式--------

APPENDI - Analysis of errors in estimation of line integrals

测量得到的数据是 I 1 I_1 I1​和 I 2 I_2 I2​的光子数。几乎所有的测量方案，光子被不同的探测器或脉冲高度分析测量，这些计数是参数为 λ 1 \lambda_1 λ1​和 λ 2 \lambda_2 λ2​的独立泊松随机变量：
λ 1 ( A 1 , A 2 ) = T ∫ S 1 ( E ) e − A 1 / E 3 − A 2 f K N ( E ) d E (A1) \lambda_1(A_1, A_2) = T\int S_1(E)e^{-A_1/E^3-A_2f_{KN}(E)} dE \tag{A1} λ1​(A1​,A2​)=T∫S1​(E)e−A1​/E3−A2​fKN​(E)dE(A1)

λ 2 ( A 1 , A 2 ) = T ∫ S 2 ( E ) e − A 1 / E 3 − A 2 f K N ( E ) d E (A2) \lambda_2(A_1, A_2) = T\int S_2(E)e^{-A_1/E^3-A_2f_{KN}(E)} dE \tag{A2} λ2​(A1​,A2​)=T∫S2​(E)e−A1​/E3−A2​fKN​(E)dE(A2)

其中$T$是积分时间。
我们希望给定 I 1 I_1 I1​和 I 2 I_2 I2​估计 A 1 A_1 A1​和 A 2 A_2 A2​并且推导 A 1 A_1 A1​和 A 2 A_2 A2​的方差表达式。可以使用极大似然估计(Van Trees 1968)，涉及到最大化假定 A 1 A_1 A1​和 A 2 A_2 A2​值测量 I 1 I_1 I1​和 I 2 I_2 I2​的概率。概率公式为：
P r ( I 1 , I 2 ∣ A 1 , A 2 ) = λ 1 I 1 e − λ 1 I 1 ! λ 2 I 2 e − λ 2 I 2 ! (A3) P_r(I_1, I_2\mid A_1, A_2) = \frac{\lambda_1^{I_1}e^{-\lambda_1}}{I_1!}\frac{\lambda_2^{I_2}e^{-\lambda_2}}{I_2!} \tag{A3} Pr​(I1​,I2​∣A1​,A2​)=I1​!λ1I1​​e−λ1​​I2​!λ2I2​​e−λ2​​(A3)

由于对数是一个单调递增的函数，我们也可以使概率函数的对数最大化
L = ln ⁡ P r ( I 1 , I 2 ∣ A 1 , A 2 ) = I 1 ln ⁡ λ 1 − λ 1 + I 2 ln ⁡ λ 2 − λ 2 − ln ⁡ ( I 1 ! I 2 ! ) (A4) L = \ln P_r(I_1, I_2\mid A_1, A_2) =I_1\ln \lambda_1 - \lambda_1+I_2\ln \lambda_2 - \lambda_2 - \ln(I_1!I_2!) \tag{A4} L=lnPr​(I1​,I2​∣A1​,A2​)=I1​lnλ1​−λ1​+I2​lnλ2​−λ2​−ln(I1​!I2​!)(A4)

当
∂ L ∂ A 1 = 0 = ∂ λ 1 ∂ A 1 ( I 1 λ 1 − 1 ) + ∂ λ 2 ∂ A 1 ( I 2 λ 2 − 1 ) (A5) \frac{\partial L}{\partial A_1} = 0 = \frac{\partial \lambda_1}{\partial A_1}(\frac{I_1}{\lambda_1} - 1) + \frac{\partial \lambda_2}{\partial A_1}(\frac{I_2}{\lambda_2} - 1) \tag{A5} ∂A1​∂L​=0=∂A1​∂λ1​​(λ1​I1​​−1)+∂A1​∂λ2​​(λ2​I2​​−1)(A5)

∂ L ∂ A 2 = 0 = ∂ λ 1 ∂ A 2 ( I 1 λ 1 − 1 ) + ∂ λ 2 ∂ A 2 ( I 2 λ 2 − 1 ) (A6) \frac{\partial L}{\partial A_2} = 0 = \frac{\partial \lambda_1}{\partial A_2}(\frac{I_1}{\lambda_1} - 1) + \frac{\partial \lambda_2}{\partial A_2}(\frac{I_2}{\lambda_2} - 1) \tag{A6} ∂A2​∂L​=0=∂A2​∂λ1​​(λ1​I1​​−1)+∂A2​∂λ2​​(λ2​I2​​−1)(A6)

时，函数取最大值
{eqA5}和{eqA6}是关于 [ I 1 λ 1 − 1 ] [\frac{I_1}{\lambda_1} - 1] [λ1​I1​​−1]和 [ I 2 λ 2 − 1 ] [\frac{I_2}{\lambda_2} - 1] [λ2​I2​​−1]的齐次线性方程组。

当系数矩阵行列式
d e t ( ∂ λ 1 ∂ A 1 ∂ λ 2 ∂ A 1 ∂ λ 1 ∂ A 2 ∂ λ 2 ∂ A 2 ) det \begin{pmatrix} \frac{\partial \lambda_1}{\partial A_1} & \frac{\partial \lambda_2}{\partial A_1} \\ \frac{\partial \lambda_1}{\partial A_2} & \frac{\partial \lambda_2}{\partial A_2} \end{pmatrix} det(∂A1​∂λ1​​∂A2​∂λ1​​​∂A1​∂λ2​​∂A2​∂λ2​​​)

非零时，解唯一：
KaTeX parse error: Undefined control sequence: \label at position 78: …1 = 0 \tag{A7} \̲l̲a̲b̲e̲l̲{eqA7}

注意这等价于由{eq9}和{eq10}定义的变换的Jacobi矩阵非零。

极大似然估计因此涉及到求解方程组：
I 1 λ 1 − 1 = 0 ⇒ I 1 = λ 1 = T ∫ S 1 ( E ) e − A 1 / E 3 − A 2 f K N ( E ) d E (A9) \frac{I_1}{\lambda_1} - 1 = 0 \Rightarrow I_1 = \lambda_1 = T\int S_1(E)e^{-A_1/E^3-A_2f_{KN}(E)} dE \tag{A9} λ1​I1​​−1=0⇒I1​=λ1​=T∫S1​(E)e−A1​/E3−A2​fKN​(E)dE(A9)

I 2 λ 2 − 1 = 0 ⇒ I 2 = λ 2 = T ∫ S 2 ( E ) e − A 1 / E 3 − A 2 f K N ( E ) d E (A10) \frac{I_2}{\lambda_2} - 1 = 0 \Rightarrow I_2 = \lambda_2 = T\int S_2(E)e^{-A_1/E^3-A_2f_{KN}(E)} dE \tag{A10} λ2​I2​​−1=0⇒I2​=λ2​=T∫S2​(E)e−A1​/E3−A2​fKN​(E)dE(A10)

这个估计的方差可以用Cramer-Rao边界来计算(Van Trees 1968, p.79)。这是可以做到的，因为对于大的样本容量，所有的极大似然估计都有渐近接近这个界的方差。为了准确地重构，必须积累大量的计数，因此在渐近区域总是使用由{eq9}和{eq10}给出的估计量。

给出了该多变量系统估计方差的Cramer-Rao边界：

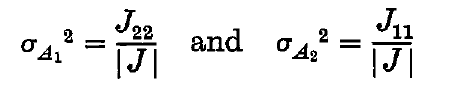
其中 J i j J_{ij} Jij​是下述矩阵的元素：
J i j = − E x [ ∂ 2 L ∂ A i ∂ A j ] , i , j = 1 , 2 (A12) J_{ij} = -E_x[\frac{\partial^2L}{\partial A_i\partial A_j}], i,j=1,2 \tag{A12} Jij​=−Ex​[∂Ai​∂Aj​∂2L​],i,j=1,2(A12)

E x E_x Ex​表示期望值。利用 I 1 I_1 I1​和 I 2 I_2 I2​的Poisson性质，有 E x [ I 1 ] = λ 1 E_x[I_1] = \lambda_1 Ex​[I1​]=λ1​， E x [ I 2 ] = λ 2 E_x[I_2] = \lambda_2 Ex​[I2​]=λ2​可以通过一些代数证明:
J 11 = 1 λ 1 ( ∂ λ 1 ∂ A 1 ) 2 + 1 λ 2 ( ∂ λ 2 ∂ A 1 ) 2 (A13) J_{11} = \frac{1}{\lambda_1}(\frac{\partial \lambda_1}{\partial A_1})^2 + \frac{1}{\lambda_2}(\frac{\partial \lambda_2}{\partial A_1})^2 \tag{A13} J11​=λ1​1​(∂A1​∂λ1​​)2+λ2​1​(∂A1​∂λ2​​)2(A13)

J 22 = 1 λ 1 ( ∂ λ 1 ∂ A 2 ) 2 + 1 λ 2 ( ∂ λ 2 ∂ A 2 ) 2 (A14) J_{22} = \frac{1}{\lambda_1}(\frac{\partial \lambda_1}{\partial A_2})^2 + \frac{1}{\lambda_2}(\frac{\partial \lambda_2}{\partial A_2})^2 \tag{A14} J22​=λ1​1​(∂A2​∂λ1​​)2+λ2​1​(∂A2​∂λ2​​)2(A14)

J 21 = J 12 = 1 λ 1 ( ∂ λ 1 ∂ A 1 ) ( ∂ λ 1 ∂ A 2 ) + 1 λ 2 ( ∂ λ 2 ∂ A 1 ) ( ∂ λ 2 ∂ A 2 ) (A15) J_{21} = J_{12} = \frac{1}{\lambda_1}(\frac{\partial \lambda_1}{\partial A_1})(\frac{\partial \lambda_1}{\partial A_2}) + \frac{1}{\lambda_2}(\frac{\partial \lambda_2}{\partial A_1})(\frac{\partial \lambda_2}{\partial A_2}) \tag{A15} J21​=J12​=λ1​1​(∂A1​∂λ1​​)(∂A2​∂λ1​​)+λ2​1​(∂A1​∂λ2​​)(∂A2​∂λ2​​)(A15)

定义
m i j = ∂ ln ⁡ λ i ∂ A j , i , j = 1 , 2 (A16) m_{ij} = \frac{\partial \ln \lambda_i}{\partial A_j} ,i,j=1,2 \tag{A16} mij​=∂Aj​∂lnλi​​,i,j=1,2(A16)

表达式{eqA13}、{eqA14}和{eqA15}可以写为：
J 11 = λ 1 m 11 2 + λ 2 m 21 2 (A17) J_{11} = \lambda_1 m_{11}^2 + \lambda_2 m_{21}^2 \tag{A17} J11​=λ1​m112​+λ2​m212​(A17)

J 22 = λ 1 m 12 2 + λ 2 m 22 2 (A18) J_{22} = \lambda_1 m_{12}^2 + \lambda_2 m_{22}^2 \tag{A18} J22​=λ1​m122​+λ2​m222​(A18)

J 12 = J 21 = λ 1 m 11 m 12 + λ 2 m 21 m 22 (A19) J_{12} = J_{21} = \lambda_1 m_{11}m_{12} + \lambda_2 m_{21}m_{22} \tag{A19} J12​=J21​=λ1​m11​m12​+λ2​m21​m22​(A19)

经过一些代数运算，可以计算得到 A 1 A_1 A1​和 A 2 A_2 A2​的方差表达式：
σ A 1 2 = ( m 12 2 / λ 2 ) + ( m 22 2 / λ 1 ) m 11 m 22 − m 12 m 21 (A20) \sigma_{A_1}^2 = \frac{(m_{12}^2/\lambda_2) + (m_{22}^2/\lambda_1)}{m_{11}m_{22} - m_{12}m_{21}} \tag{A20} σA1​2​=m11​m22​−m12​m21​(m122​/λ2​)+(m222​/λ1​)​(A20)

σ A 2 2 = ( m 11 2 / λ 2 ) + ( m 22 2 / λ 1 ) m 11 m 22 − m 12 m 21 (A21) \sigma_{A_2}^2 = \frac{(m_{11}^2/\lambda_2) + (m_{22}^2/\lambda_1)}{m_{11}m_{22} - m_{12}m_{21}} \tag{A21} σA2​2​=m11​m22​−m12​m21​(m112​/λ2​)+(m222​/λ1​)​(A21)

假设 λ 1 ≈ I 1 \lambda_1 \approx I_1 λ1​≈I1​， λ 2 ≈ I 2 \lambda_2 \approx I_2 λ2​≈I2​，并且使用{eqA1}和{eqA2}幂级数形式，可以得到：
λ 1 ( A 1 , A 2 ) = e − b 0 − b 1 A 1 − b 2 A 2 − b 3 A 1 2 − b 4 A 2 2 − b 5 A 1 A 2 − b 6 A 1 3 − b 7 A 2 3 (A22) \lambda_1(A_1, A_2) = e^{-b_0 - b_1A_1 - b_2A_2 - b_3A_1^2- b_4A_2^2 - b_5A_1A_2 - b_6A_1^3 - b_7A_2^3} \tag{A22} λ1​(A1​,A2​)=e−b0​−b1​A1​−b2​A2​−b3​A12​−b4​A22​−b5​A1​A2​−b6​A13​−b7​A23​(A22)

λ 2 ( A 1 , A 2 ) = e − c 0 − c 1 A 1 − c 2 A 2 − c 3 A 1 2 − c 4 A 2 2 − c 5 A 1 A 2 − c 6 A 1 3 − c 7 A 2 3 (A23) \lambda_2(A_1, A_2) = e^{-c_0 - c_1A_1 - c_2A_2 - c_3A_1^2- c_4A_2^2 - c_5A_1A_2 - c_6A_1^3 - c_7A_2^3} \tag{A23} λ2​(A1​,A2​)=e−c0​−c1​A1​−c2​A2​−c3​A12​−c4​A22​−c5​A1​A2​−c6​A13​−c7​A23​(A23)
方差可以从这些表达式中计算出来。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！