总结 分布 --- 贝叶斯 --- 信息熵
分布
-
联合分布
- 定义:2个随机变量联合表示起来称为联合概率
- 举一个例子:这里有一些扑克牌,接下来我们来求一下联合分布


- 这里的人头指的是:J,Q,K
- 这里的数字指的是:A-9
- 这里的红色指的是:红桃,方片
- 这里的黑色指的是:梅花,黑桃
- 联合分布也就是从2个方向描述比如上面的1/16,就是既是黑色又是人头的个数占扑克牌的总个数
-
边缘分布
- 还是上面的扑克牌,我们再来求一下边缘分布

- 而边缘分布是从1个方向上进行描述比如9/16,就是红色占扑克牌总数的占比,不用管它是数字还是人头
-
离散分布
二项分布- 二项分布:每次产生的结果相互独立,成功的概率保持不变的事件的成功的次数,就是------->二项分布
- 公式:

- 其中n表示实验总次数,k表示成功的次数
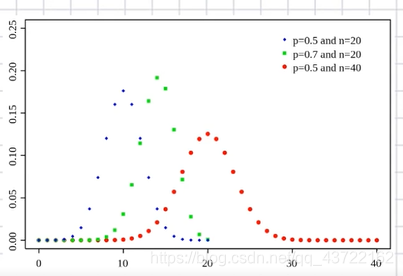
- 横轴表示:实验成功的次数
- 纵轴表示:实验成功的概率
- 当成功的次数相同时,从图上可知实验成功的概率越大,图像形状越陡峭
- 当成功的概率相同时,从图上可知实验成功的次数越大,图像形状越平缓
超几何分布
- 超几何分布:它和二项分布还有一些渊源,在一个盒子里,放着2种颜色的球,一种黑色,一种白色,求随机抽取,记录它是不是黑球的概率,重点来了,如果每次取出并把球放回去,重复这个过程,看看有多少次取出的是黑球,这一计数遵循二项分布,如果不放回取出的球,那么这一计数就是超几何分布,说白了,就是取出不放回的计数,就是超几何分布;而取出放回就是二项分布
- 公式:

- n表示样本的数量
- k表示不合格的个数

- 横轴表示不合格的数量
- 纵轴表示概率密度函数
- 当总次数一致时,实验数越多,概率密度的峰值越低
- 当总次数一致时,不合格数越多,概率密度的峰值也越低
多项分布:二项分布的一个扩展,二项分布是一个单变量分布,多项分布是一个多变量分布
- 公式

- 比如:投掷骰子,1的概率,2的概率,3的概率等等,就是一个多项分布
几何分布:在第一次出现正面之前,出现多上次背面的分布也就是结果本身失败的实验次数
- 公式
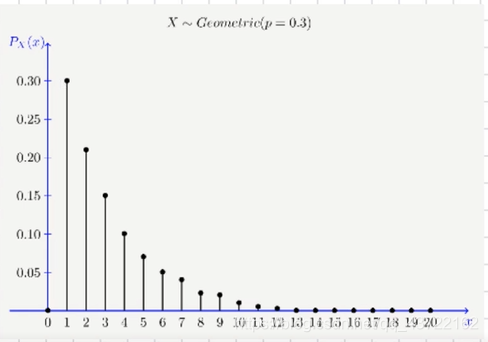
- 横轴表示第n次成功,失败的次数
- 纵轴表示成功的概率
泊松分布:表示事件在单位时间内发生n次的概率
-
公式
-

-
λ表示单位时间内发生的次数
-
公式推导过程
-
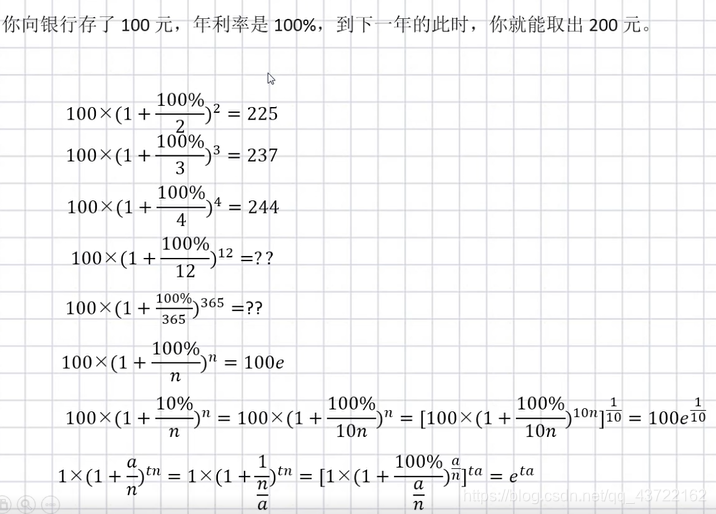
-
e:增长的极限 ≈ 2.71828
-
最后不管年利率,月利率,天利率,最后的结果都在e的边缘
-
已知莫医院平均一天里有λ名诞生儿,一天有86400秒,假设新生儿不可能在同一秒诞生,且每个诞生儿的概率都是相同的,均为 (λ/86400)
-
事件总数n = 86400,成功的概率 = (λ/86400) ,失败的概率 = 1- (λ/86400),每日出生k个婴儿,带入公式为:
-

-
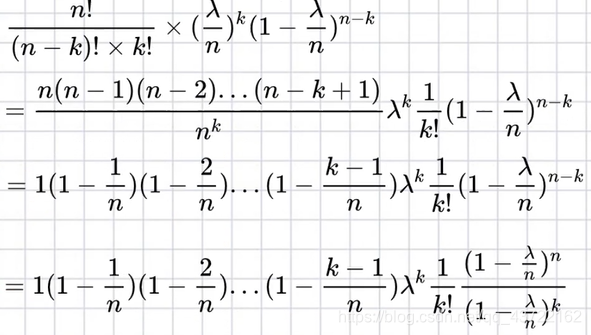
-
当n趋向于无穷大,k和λ趋向于无穷小时,结合上面的年利率的例子
-
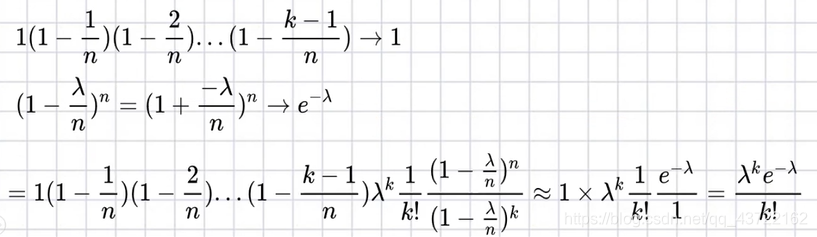
-
连续分布
指数分布:泊松分布研究的时一个时间段内发生的次数,而指数分布则研究的是独立事件放生的时间间隔
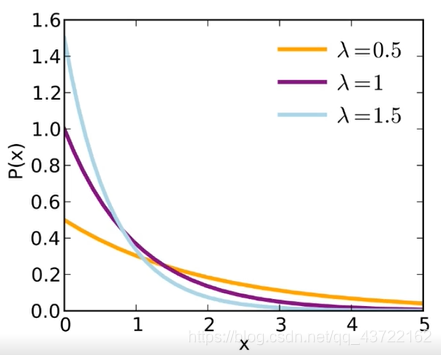
- 横轴表示发生的时间间隔
- 纵轴表示发生的概率
正太概率分布:描述连续性随机变量的一种分布
- 公式

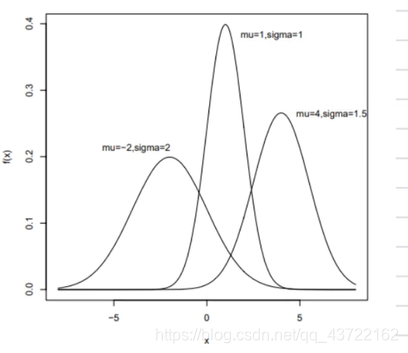
- 横轴表示连续区间
- 纵轴表示发生的概率
拉普拉斯分布:双边指数分布
- 公式

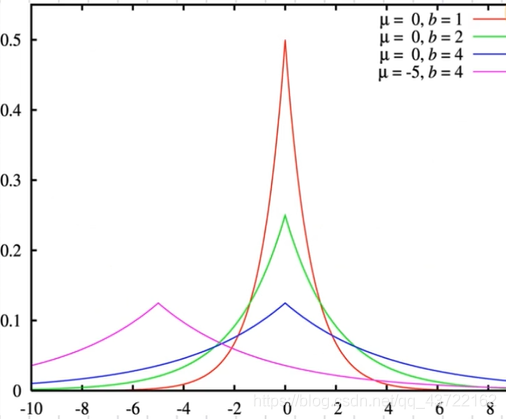
- 横轴表示连续区间
- 纵轴表示发生的概率
贝叶斯
- 贝叶斯:用来描述两个条件概率之间的关系,比如 P(A|B) 和 P(B|A)。按照乘法法则,可以立刻导出:P(A∩B) = P(A)*P(B|A)=P(B)*P(A|B)。如上公式也可变形为:P(A|B)=P(B|A)*P(A)/P(B)
- 公式

- 全概率公式

- 条件概率公式

朴素贝叶斯:特征相互独立,简化贝叶斯方法的一种分类方法
- p(真)和p(假)分母都一样,所以分母不用算(比较大小)
信息熵
大数据思维实质:就是提供有价值的信息降低信息熵
信息熵:是在结果出来之前对可能产生的信息量的期望
信息熵:信息量的期望
-
公式
-

-
小集合公式
-

-
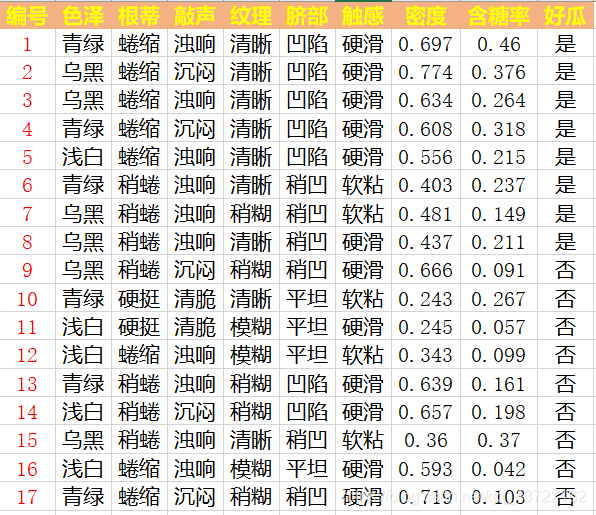
数据集D中有V个离散属性划分为v个小集合的信息熵
-
数据集
-
-
信息熵

联合熵:两个随机变量X,Y的联合分布,用H(X,Y)表示
条件熵:在得知某一确定信息的基础上获取另一个信息时所获得的信息量
互信息:应用场景—>相关性:知道一个对知道另一个帮助有多大
推导公式过程:
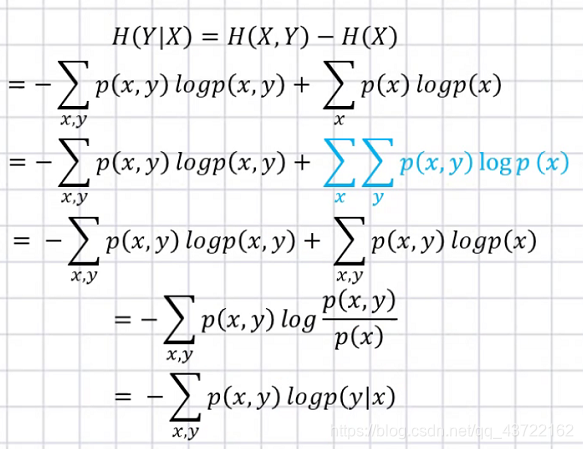
- 其中p(x) —>

本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!