十大排序算法(c语言实现)（二）

十大排序算法(c语言实现)（二）

归并排序、快速排序、堆排序对比分析与c语言实现

文章目录

• 十大排序算法(c语言实现)（二）
• 前言
• 一、归并排序
• • 1.原理
  • 2.实现
  • 3.算法分析
• 一、快速排序
• • 1.原理
  • 2.实现
  • 3.算法分析
• 一、堆排序
• • 1.原理
  • 2.实现
  • 3.算法分析
• 总结

前言

上一节的排序算法都是基于线性表进行实现的，算法的时间复杂度的极限就为希尔排序o(n^1.3)。这节的算法通过树结构进行实现，能够进一步改进算法的时间复杂度。

一、归并排序

1.原理

对数组不断递归，分成左右两部分，直到分成一个数，递归终止。然后再将左右两两合并排序。
排序过程如下图：

算法的分组和归并可以用二叉树的后序遍历方式实现。主要的算法就是两个数组的合并排序。
合并排序过程如下图：

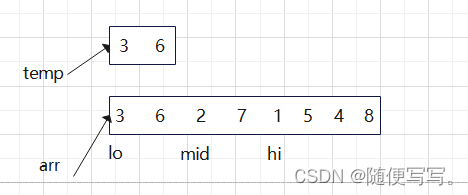
对左边数组3 6，右边数组2 7 进行归并排序。对3 2进行比较，将较小的2放在索引0位置，右边数组规模减一；将3 7进行比较，将较小的3放在索引1，左边数组规模减一；对6 7 进行比较，将较小的6放在索引2，左边数组遍历完，直接将右边数组放到原数组。两个数组归并后2 3 6 7。

2.实现

void merge(int* arr, int lo, int mid, int hi)
{int llen = mid - lo;int rlen = hi - mid;int* temp = (int*)malloc(sizeof(int) * llen);//分配空间用于存储[lo.hi)中的值，防止覆盖原数组																			int index = lo;for (int i = 0; i < llen; i++){temp[i] = arr[index++];}//i指向临时的分配空间，j指向合并数组的开始，k指向合并数组右边部分的开始for (int i = 0, j = lo, k = mid; j < hi;){if (i < llen && (!(k < hi) || (temp[i] <= arr[k]))){//如果左边数组的数字没取完并且右边数组取完了或者左边数组的数字小于右边数组的数字则将左边数组的数字合并到主数组当中arr[j++] = temp[i++];}if (k < hi && (!(i < llen) || (arr[k] < temp[i]))){arr[j++] = arr[k++];}}free(temp);
}
void merge_sort_internal(int* arr,int lo,int hi)
{if ((hi - lo) < 2) return; //当只有一个数时递归结束int mid = (lo + hi)/2;//中间节点merge_sort_internal(arr, lo, mid);//遍历左子树merge_sort_internal(arr, mid, hi);//遍历右子树merge(arr, lo, mid, hi);//数组合并操作}
void merge_sort(int* arr, int len)
{int lo = 0;int hi = len;merge_sort_internal(arr, lo, hi);
}

3.算法分析

时间复杂度： 归并排序利用数组模拟二叉树的后续遍历方式，所以时间复杂度和二叉树的遍历一致，算法最坏情况、最好情况和平均复杂度都是o(nlogn)。
空间复杂度： 在实现过程中需要分配额外的空间来存储左半部分的数组，空间复杂度为o(n)。
稳定性: 合并操作不会改变相同数字的相对次序，为稳定排序算法。

一、快速排序

1.原理

不断以数组第一个数字作为轴点，找到轴点的索引，可以将数组分为左右两个数组继续遍历，当只有一个节点时则数组有序，结束递归。
算法的递归如下：

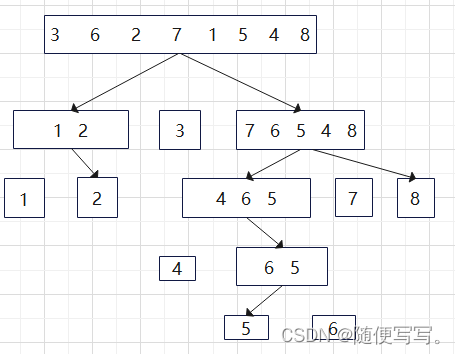
算法的递归可以用二叉树的中序遍历来实现，对中间节点的处理为找到轴点。
找轴点的算法如下：
找到算法3的轴点：将3不断与数组最右边进行比较，1<3将1放到之前3的位置；然后继续从左边比较，6>3将6放到之前1的位置；然后继续从上一次的右边进行比较，2<3将2放入之前6的位置；最后范围缩小到只有一个数，将轴点3放入。

2.实现

int partition(int* arr, int lo,int hi)
{      //实现为左闭右闭区间int mid = lo + rand() % (hi - lo+1);swap(&arr[lo], &arr[mid]);//随机选择轴点int temp = arr[lo];while (lo < hi){while (lo < hi){if (temp < arr[hi])//轴点小于右边数组则不断缩小hi的索引{hi--;}else {arr[lo++] = arr[hi];//当轴点不大于hi对应的值时将arr[hi]移至左边break;//退出继续移动左边的值}}while (lo < hi){if (temp > arr[lo])//轴点大于左边数组则不断增大lo索引{lo++;}else {arr[hi--] = arr[lo];//轴点小于等于arr[lo]将arr[lo]移至右边break;//退出继续移动右边的值}}}arr[lo] = temp;//退出循环后lo左边的值都小于轴点右边的值都大于轴点,lo就为轴点的值return lo;
}
void quick_sort_internal(int* arr, int lo, int hi)
{    //左闭右开区间if (lo >= hi) return; //当lo==hi时空间中没有数据结束递归int mid = partition(arr, lo, hi-1);//选择一个轴点完成插入操作quick_sort_internal(arr, lo, mid);//递归遍历左子树quick_sort_internal(arr, mid + 1, hi);//递归遍历右子树
}
void quick_sort(int* arr, int len)
{int lo = 0;int hi = len;quick_sort_internal(arr, lo, hi);
}

3.算法分析

时间复杂度： 最坏情况为数组的次序接近有序，每次选择最小值作为轴点，要通过n次比较将轴点放回原点，继续遍历右子树，这时左子树为空，二叉树退化成线性结构，所以这时的时间复杂度为o(n^2)。最好情况和平均复杂度都为o(nlogn)。
空间复杂度： 该算法实现没有分配额外空间，属于就地排序，空间复杂度为o(1)。
稳定性: 在移动过程当中会改变两个相同数字的相对次序，属于不稳定性排序。

一、堆排序

1.原理

算法关键是对最大堆的创建，利用floyd算法通过自下而上的下虑操作进行建堆，时间复杂度最小。
建堆过程：
对父节点3进行下虑操作

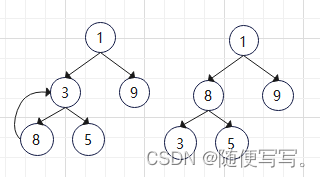
对父节点1进行下虑操作：

建堆完成后不断取最大值放在数组最后一位：

通过不断将最大值和最后一位的值交换，在对根节点进行下虑，每次有序数组增加一，堆的规模减一。

2.实现

void down_adjust(int* arr, int parent_index, int length)
{  //对节点的下虑int temp = arr[parent_index]; // 父节点int child = 2 * parent_index + 1; // left childwhile (child < length) {if (child + 1 < length && arr[child] < arr[child + 1]) {child++;//找到最大孩子}if (temp >= arr[child]) {break; //父节点比孩子大直接退出}arr[parent_index] = arr[child];parent_index = child;child = 2 * child + 1;//继续下虑操作}arr[parent_index] = temp;
}void make_heap(int* arr, int length)
{  //自下而上的下虑建堆int end_index = length - 1;//找到最后一个父节点for (int i = (end_index - 2) / 2; i >= 0; i--) {down_adjust(arr, i, length);//遍历所有的父节点进行下虑}
}
void heap_sort(int* arr, int length)
{make_heap(arr, length); //建最大堆for (int i = length - 1; i >= 0; i--){swap(&arr[0], &arr[i]);//取出最大值与最后一个数交换down_adjust(arr, 0, --length);//继续对第一个数进行下虑操作，无序数组规模减一}
}

3.算法分析

时间复杂度： 建堆的时间复杂对为o(n)，排序要对N个数进行下虑操作，由于堆为完全二叉树，所以最好情况、最坏情况和平均复杂度相同，都为o(nlogn)。
空间复杂度： 为就地排序，空间复杂度为o(1)。
稳定性： 为不稳定算法。

总结

归并排序、快速排序、堆排序算法都是基于二叉树进行排序，性能相比于线性表较好，时间复杂度都为o(nlogn)。虽然三种算法的时间复杂度都为o(nlogn)，但是数据规模巨大时，快速排序更有优势，因为数据规模巨大后，归并排序的合并操作需要消耗大量时间，堆排序的下虑操作需要访问父节点和子节点，访问的索引跨度较大，而快速排序只需访问相邻的索引值。虽然快速排序的最坏情况时间复杂度为o(n^2)，但出现的概率极小。所以快速排序应用更广泛，比如用在linux下的排序算法和STL的排序算法。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！