矩阵论—线性子空间、生成子空间、核空间、零度、子空间的交与和、直和
线性子空间定义
如果
，V1称为平凡子空间，否则称为非平凡子空间。
生成子空间
核空间、零度
解：
rank(A)=2; n(A)=N-rank(A)=3-2=1，这里N表示的是未知量的个数。
n(A)也可以理解为基础解系的个数，即基础解系中有几个向量。
结论：
（1）rnak(A) + n(A) = A 的列数
（2）n(A) - n(A^T) = (A的列数) -（A的行数）
子空间的交与和
例题：
直和
综合例题：
解：
再例如：
再例如：
再求两个子空间交的维数：
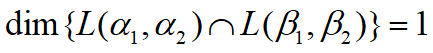
本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！