期权专题8:隐含波动率(BSM二分法)
目录
1. 定义及方法
1.1 隐含波动率
1.2 BSM二分法
2. 代码实现
2.1. 数据获取
2.2 计算数值
2.3 批量测算及作图
2.4 完整代码
3. 总结
免责声明:本文由作者参考相关资料,并结合自身实践和思考独立完成,对全文内容的准确性、完整性或可靠性不作任何保证。同时,文中提及的数据仅作为举例使用,不构成推荐;文中所有观点均不构成任何投资建议。请读者仔细阅读本声明,若读者阅读此文章,默认知晓此声明。
1. 定义及方法
1.1 隐含波动率
隐含波动率(简称隐波)是将期权实际的市价带入BSM模型,反推出来的数值。隐波反映了整个市场参与者对于对于未来不确定性或风险水平的预期。如果隐波的数值较前期上涨,说明大家预期未来市场波动将会增大,反之则减小。
1.2 BSM二分法
基于BSM模型计算隐波的方法有多种(各种方式测算出的结果差异均不大,不再逐一介绍),本文主要选择二分法。选择二分法的原因主要有两点:1.思路简单,理解起来比较容易;2.速度较快,同时精准度也较高。
BSM计算期权价格时采用的波动率是常数,隐波的求解其实就是在已知期权价格的情况下反解波动率的值。由于BSM的公式比较复杂,所以使用解析法难度比较高,因此选择模拟法的思路来求解。模拟法的思路是:在BSM模型中传入不同的波动率数值,当计算得出的期权价格等于实际市价的时候,对应的波动率即是该期权当前的隐含波动率。
由于模拟法本身需要大量的数据进行循环,因此在模拟法的基础上叠加‘夹逼定理’的思路,即采用二分法来降低模拟循环的次数,提高运算的效率。下面,使用一个流程图来展示BSM二分法的思路和步骤:
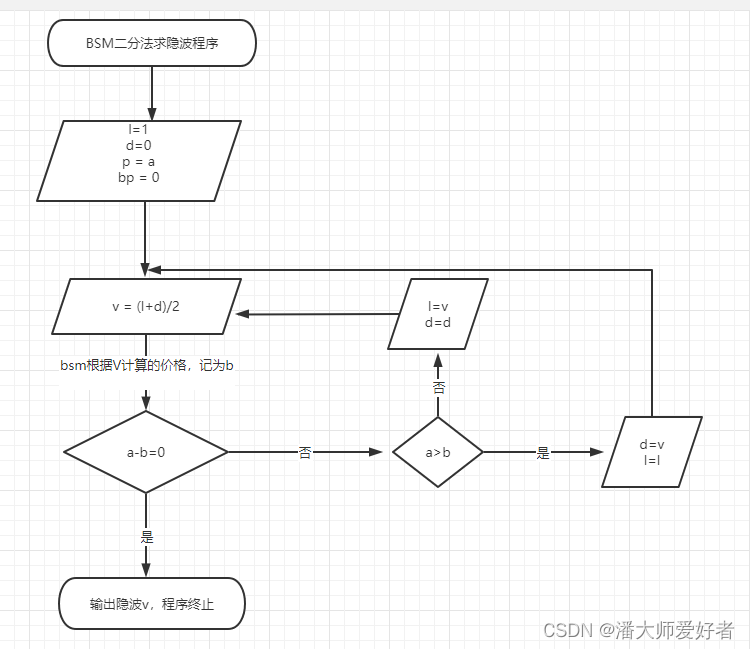
上图中,l表示波动率上限,初始值为1;d表示波动率,下限初始值为0。p表示期权真实市价,值为a,bp表示BSM模型计算出的期权价格,初始值为0。v表示传入的波动率值。其他的BSM模型所需参数根据期权要素设置为定参,此处不再传入。
根据流程,初始传入的V值为0.5(上限1和下限0的均值),根据V值BSM模型计算出的价格bp值为b。如果a和b的值相等,则说明V为期权对应的隐含波动率,程序结束
如果啊a,b不相等,则需要继续寻找波动率的合适值。若a>b,说明BSM测算出来的值偏低,即设置的波动率偏低,真实的波动率应该大于0.5,将波动率下限d设置为0.5,上限任然不变,此时对应的新的波动率为0.75,传入原流程继续循环。 同样地,若a 需要注意的是,实际过程中程序测算的b值可能是无限小数,因此在值的大小比较上,应该将a=b的条件切换为|a-b| 由于需要使用到BSM模型,因此先放一下前期写的BSM模型的代码(对此处不太熟悉的读者可以查看前期的文章期权专题6),代码如下: 接下来,使用akshare开源api获取2023年7月3日收盘后的50ETF看涨期权的合约数据,整体的代码如下: 对应得到的结果如下(需要注意,这里获取的是实时的数据,不同时点获取的数据可能不同): 在得到了原始数据之后,通过市价以及相应的参数来计算对应隐波的值。此时点,对应的50ETF的价格是2.577,合约剩余的天数为85,取无风险利率为2.2%。对应的代码如下: 对应得到的结果是16.29%,同花顺查询的同期隐波数据约为16.27%,因此测算出的结果差异非常小,说明代码整体的运算逻辑是可行的。这里提一点,代码中将测算期权价值和实际的期权市价差异设置为万分之一以内,个人感觉这个误差已经非常小了。当然这个差异的设定因所需而异。 至此,BSM二分法测算隐含波动率已经复现完毕。对于后文关于批量测算的代码,读者可以按需选择性阅读。 在测算了单个合约的隐含波动率后,通过继续迭代,获取多个其他要素相同,仅执行价不同的合约对应的隐含波动率。代码如下: 对应得到的结果如下: 上述得到了对应多个不同执行价的2309合约的隐含波动率,继续更换约(2308,2312),得到新的隐含波动率数据。由于是盘中获取的数据,数据本身是动态的,因此后期运行代码获取的数据较前文会有所差别,但这不影响最终的测算。整体的代码如下: 最后,得到的结果如下: 将上述结果作图,对应代码如下: 对应得到的结果如下图: 由于各类测算期权隐含波动率的方法得到的结果基本一致,因此对于这些方法不存在优劣的比较,更多只是个人的偏好,所以此处不在对BSM二分法作出评价。 本文代码相对冗长,一方面是为了展现批量测算隐波的方法,另一方面是为了后续‘波动率微笑’专题做一些铺垫,对此有兴趣的读者可以持续关注。 本期分享结束,有何问题随时交流。 免责声明:本文由作者参考相关资料,并结合自身实践和思考独立完成,对全文内容的准确性、完整性或可靠性不作任何保证。同时,文中提及的数据仅作为举例使用,不构成推荐;文中所有观点均不构成任何投资建议。请读者仔细阅读本声明,若读者阅读此文章,默认知晓此声明。 2. 代码实现
2.1. 数据获取
import akshare as ak
import numpy as np
from scipy.stats import norm
import pandas as pddef get_constant_value(in_value, fix_value):# 当参数数值未传入时,取默认值if in_value == None:out_value = fix_valueelse:out_value = in_valuereturn out_valuedef BSM_option_price(d_type, S = None, K = None, vol = None, T = None, r = None ):'''BSM-期权定价模型----------d_type:str,期权类型,call/putS:float,标的资产价格,默认值为100K:float,行权价格,默认值为120vol:float,年化波动率,默认值为0.2T:float,剩余期限(折算成年),默认值为0.5r:float,连续复利无风险利率,默认值为0.03-------'''S1 = get_constant_value(S, 100)K1 = get_constant_value(K, 120)vol1 = get_constant_value(vol, 0.2)T1 = get_constant_value(T, 0.5)r1 = get_constant_value(r, 0.03)value = vol1 * np.sqrt(T1)d1 = (np.log(S1/K1) + (r1 + 0.5*vol1**2) * T1)/valued2 = d1 - valuedis_value = K1 * np.exp(-r1 * T1)if d_type == 'call':option_value = S1 * norm.cdf(d1) - dis_value * norm.cdf(d2)elif d_type == 'put':option_value = dis_value * norm.cdf(-d2) - S1 * norm.cdf(-d1)out_value = option_valuereturn out_valuedef get_data(dir, year_month):'''获取50ETF期权合约数据Parameters----------year_month:str,合约年月份,例如'2309'dir:str,期权方向,call/putReturns:DataFrame'''option_data = ak.option_finance_board(symbol="华夏上证50ETF期权", end_month=year_month)# 获取期权方向option_data['期权方向'] = option_data['合约交易代码'].apply(lambda x: 'call' if x[6:7] == "C" else 'put')test_data = option_data.loc[option_data['期权方向'] == dir]return test_dataif __name__ == '__main__':dir = 'call'year_month = '2309'data = get_data(dir, year_month)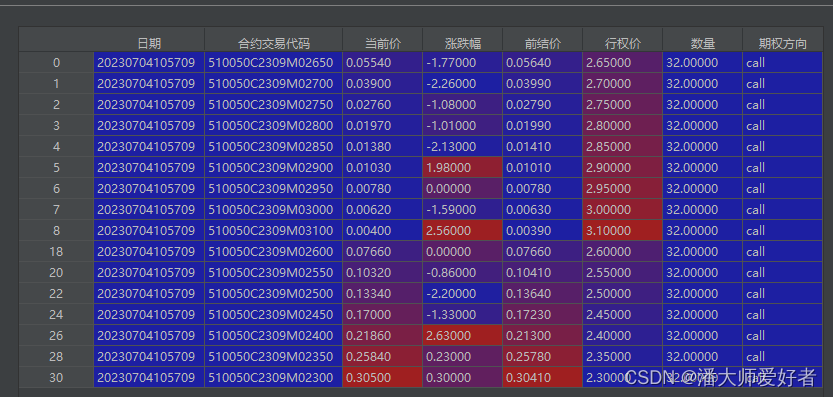
2.2 计算数值
def get_implied_volatility(value, S, K, T, r):'''BSM模型二分法计算隐含波动率----------value:float,期权市价S:float,标的资产价格K:float,行权价格T:float,剩余期限(折算成年)r:float,连续复利无风险利率-------'''max_vol = 1min_vol = 0test_value = 0test_vol = (max_vol + min_vol) / 2while abs(test_value - value) > 0.00001:print(test_vol, abs(test_value - value))test_value = BSM_option_price('call', S, K, test_vol, T, r)if test_value - value > 0:max_vol = test_voltest_vol = (max_vol + min_vol) / 2else:min_vol = test_voltest_vol = (max_vol + min_vol) / 2implied_volatility = round(test_vol,4)return implied_volatilityif __name__ == '__main__':dir = 'call'year_month = '2309'data = get_data(dir, year_month)T = 85 / 365r = 0.022S = 2.577K = data['行权价'].values[0]value = data['当前价'].values[0]test = get_implied_volatility(value, S, K, T, r)2.3 批量测算及作图
def get_batch_vol(data,T):'''批量获取合约的隐含波动率----------data:DataFrame,期权行情数据T:float,剩余期限(折算成年)Returns:list,批量获取的波动率序列-------'''r = 0.022S = 2.577vol_list = []for num in range(0, len(data)):K = data['行权价'].values[num]value = data['当前价'].values[num]one_vol = get_implied_volatility(value, S, K, T, r)vol_list.append(one_vol)return vol_listif __name__ == '__main__':dir = 'call'year_month = '2309'data = get_data(dir, year_month)T = 85 / 365vol_list = get_batch_vol(data,T)data['隐含波动率'] = vol_list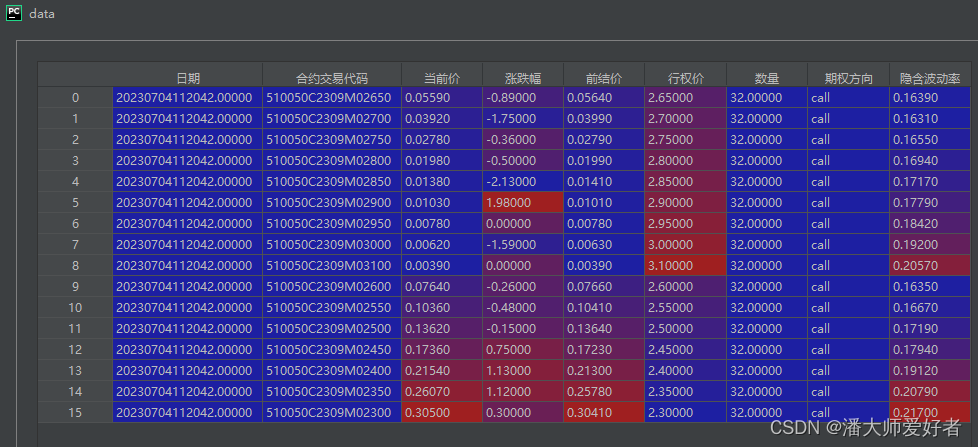
if __name__ == '__main__':dir = 'call'year_month_list = ['2308', '2309', '2312']T_list = [50, 85, 176]all_df = pd.DataFrame()for n in range(0,len(T_list)):year_month = year_month_list[n]data1 = get_data(dir, year_month)T1 = T_list[n] / 365vol_list1 = get_batch_vol(data1,T1)one_df = pd.DataFrame({'行权价':data1['行权价'],year_month+'隐含波动率':vol_list1})if all_df.empty:all_df = all_df.append(one_df)else:all_df = pd.merge(all_df,one_df,how='inner',on='行权价')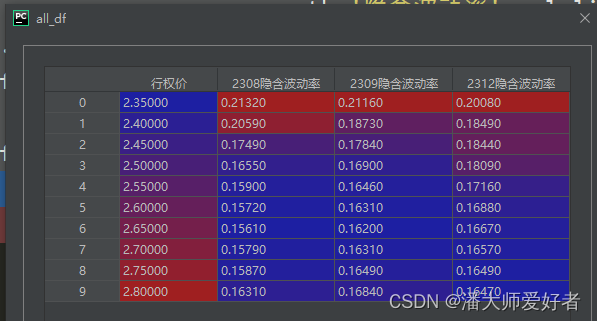
import matplotlib.pyplot as pltplt.rcParams['font.sans-serif'] = ['Microsoft YaHei']plt.rcParams['axes.unicode_minus'] = Falsefor year_month in year_month_list:plt.plot(all_df['行权价'], all_df[year_month+'隐含波动率'], label=year_month)plt.legend(loc='best')plt.show()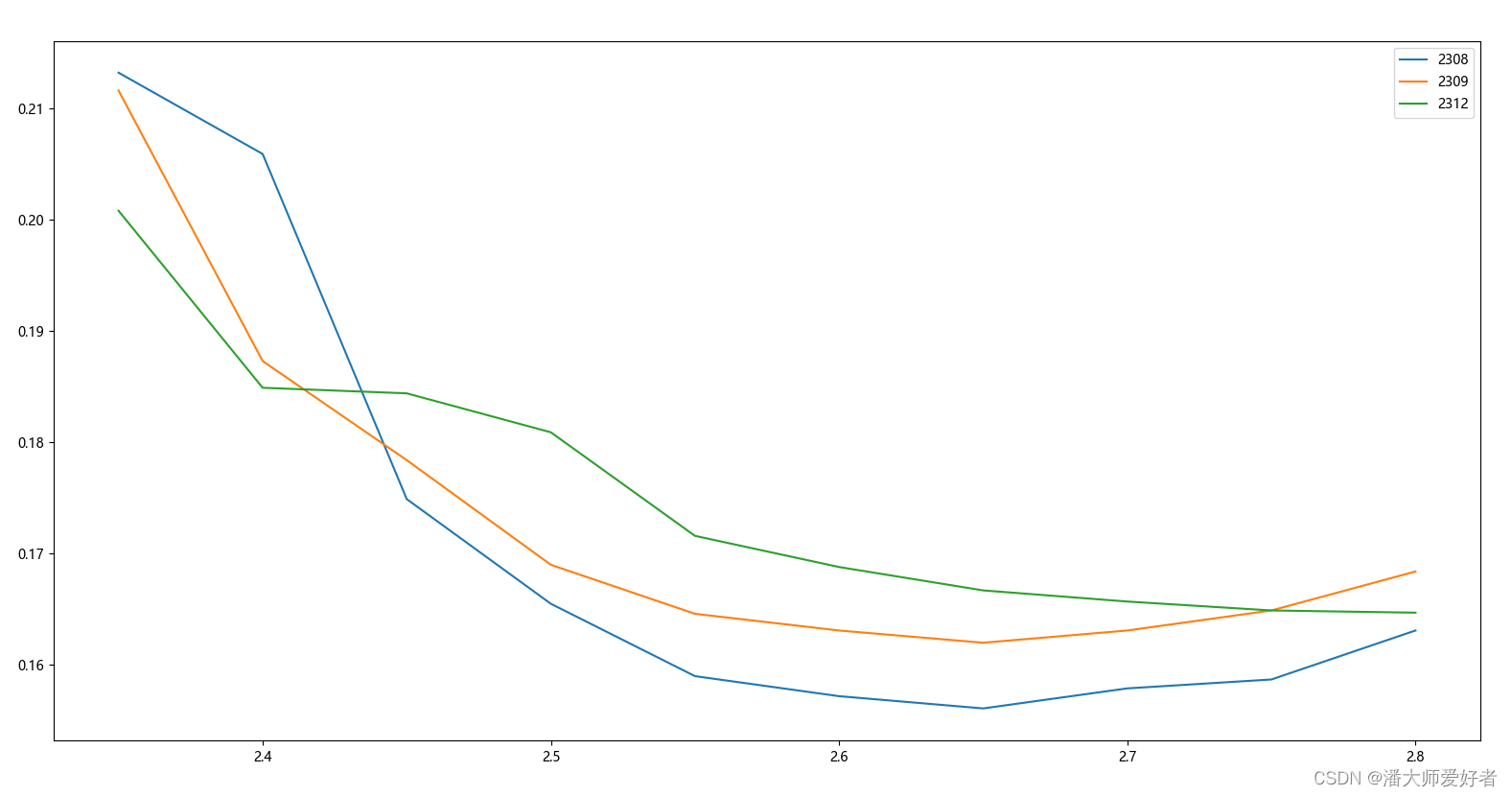
2.4 完整代码
import akshare as ak
import numpy as np
from scipy.stats import norm
import pandas as pd
import matplotlib.pyplot as pltdef get_constant_value(in_value, fix_value):# 当参数数值未传入时,取默认值if in_value == None:out_value = fix_valueelse:out_value = in_valuereturn out_valuedef BSM_option_price(d_type, S=None, K=None, vol=None, T=None, r=None):'''BSM-期权定价模型----------d_type:str,期权类型,call/putS:float,标的资产价格,默认值为100K:float,行权价格,默认值为120vol:float,年化波动率,默认值为0.2T:float,剩余期限(折算成年),默认值为0.5r:float,连续复利无风险利率,默认值为0.03-------'''S1 = get_constant_value(S, 100)K1 = get_constant_value(K, 120)vol1 = get_constant_value(vol, 0.2)T1 = get_constant_value(T, 0.5)r1 = get_constant_value(r, 0.03)value = vol1 * np.sqrt(T1)d1 = (np.log(S1 / K1) + (r1 + 0.5 * vol1 ** 2) * T1) / valued2 = d1 - valuedis_value = K1 * np.exp(-r1 * T1)if d_type == 'call':option_value = S1 * norm.cdf(d1) - dis_value * norm.cdf(d2)elif d_type == 'put':option_value = dis_value * norm.cdf(-d2) - S1 * norm.cdf(-d1)out_value = option_valuereturn out_valuedef get_data(dir, year_month):'''获取50ETF期权合约数据Parameters----------year_month:str,合约年月份,例如'2309'dir:str,期权方向,call/putReturns:DataFrame'''option_data = ak.option_finance_board(symbol="华夏上证50ETF期权", end_month=year_month)# 获取期权方向option_data['期权方向'] = option_data['合约交易代码'].apply(lambda x: 'call' if x[6:7] == "C" else 'put')test_data = option_data.loc[option_data['期权方向'] == dir]return test_datadef get_implied_volatility(value, S, K, T, r):'''BSM模型二分法计算隐含波动率----------value:float,期权市价S:float,标的资产价格K:float,行权价格T:float,剩余期限(折算成年)r:float,连续复利无风险利率-------'''max_vol = 1min_vol = 0test_value = 0test_vol = (max_vol + min_vol) / 2while abs(test_value - value) > 0.00001:print(test_vol, abs(test_value - value))test_value = BSM_option_price('call', S, K, test_vol, T, r)if test_value - value > 0:max_vol = test_voltest_vol = (max_vol + min_vol) / 2else:min_vol = test_voltest_vol = (max_vol + min_vol) / 2implied_volatility = round(test_vol, 4)return implied_volatilitydef get_batch_vol(data, T):'''批量获取合约的隐含波动率----------data:DataFrame,期权行情数据T:float,剩余期限(折算成年)Returns:list,批量获取的波动率序列-------'''r = 0.022S = 2.577vol_list = []for num in range(0, len(data)):K = data['行权价'].values[num]value = data['当前价'].values[num]one_vol = get_implied_volatility(value, S, K, T, r)vol_list.append(one_vol)return vol_listif __name__ == '__main__':dir = 'call'year_month_list = ['2308', '2309', '2312']T_list = [50, 85, 176]all_df = pd.DataFrame()for n in range(0, len(T_list)):year_month = year_month_list[n]data1 = get_data(dir, year_month)T1 = T_list[n] / 365vol_list1 = get_batch_vol(data1, T1)one_df = pd.DataFrame({'行权价': data1['行权价'],year_month + '隐含波动率': vol_list1})if all_df.empty:all_df = all_df.append(one_df)else:all_df = pd.merge(all_df, one_df, how='inner', on='行权价')plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']plt.rcParams['axes.unicode_minus'] = Falsefor year_month in year_month_list:plt.plot(all_df['行权价'], all_df[year_month + '隐含波动率'], label=year_month)plt.legend(loc='best')plt.show()
3. 总结
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!
