一种Toeplitz协方差矩阵重构的波达方向估计方法
From: A Toeplitz Covariance Matrix Reconstruction Approach for Direction-of-Arrival Estimation
IEEE TRANSACTIONS ON VEHICULAR TECHNOLOGY, VOL. 66, NO. 9, SEPTEMBER 2017
目录
主要内容
模型与实现
ULA
SLA
有限快拍效应
MATLAB代码
对偶优化
主要内容
常见的两种DOA估计方法:基于子空间的方法和基于稀疏性的方法。
基于子空间的方法:信源数目大于阵元数目时无法工作
基于稀疏性的方法:基失配或网格失配
提出一种适用于ULA或SLA的协方差矩阵重构法(CMRA)来实现DOA估计
模型与实现
ULA
接收信号:

协方差矩阵:
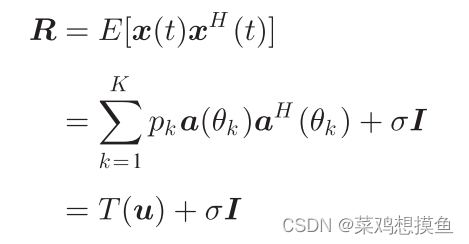
其中T为Hermitian Toeplitz矩阵:
![]()
多快拍下协方差矩阵为:

由于有限快拍数,因此该协方差矩阵包含误差,设误差分量为:

随着快拍数的增加,互相关项变小,因此E的F范数也会变小。诚然,误差分量E会导致识别错误的信号子空间,从而在MUSIC频谱中产生不正确的峰值。
因此,对T的估计非常重要(LRMR)。
对T的LRMR问题可以表述为:
![]()
因为门限参数很难确定,因此考虑一个替代约束。
考虑到vec(E)服从渐近正态分布:
![]()
其中:
![]()
可用以下进行估计:
![]()
因此有:
![]()
进而有:
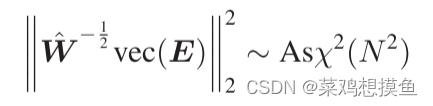
因此,下式将以1-p的概率成立:
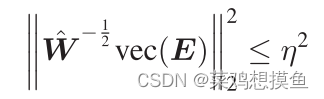
其中,η取决于N与p。因此,之前的优化问题可以重新表述为:
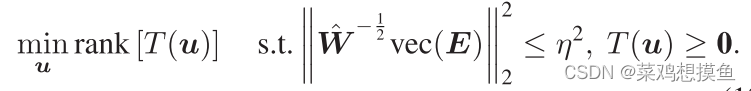
注:η由p决定。为什么选择η(或p)而非之前的参数c呢?因为p较之c有更小的动态范围。
诚然,这个问题依然是一个NP-hard问题。考虑其凸松弛,用核范数或半正定矩阵的迹范数来代替。
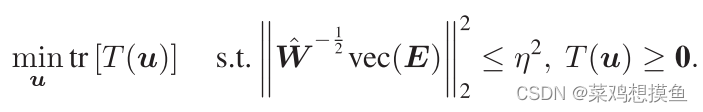
为了方便,假设噪声能量可以由最小的特征值进行估计。
得到T之后,可以用MUSIC等常规算法进行doa估计。该方法对于相干信源时效果一般,可以考虑将平滑技术引入CMRA。
SLA
SLA接收信号可以表示为:
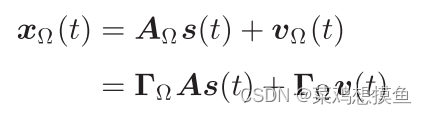
其中Ω为SLA阵元位置集合。AΩ表示对应于Ω的阵列流形。A为对应Ω的均匀阵列流形,Γ为阵列流形选择矩阵。
例如设Ω={1,2,5,7},则有:

协方差矩阵为:
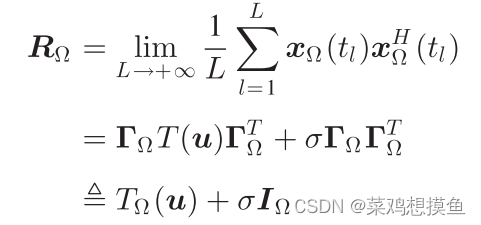
同理有协方差矩阵估计(有限快拍)、误差分量、方差矩阵为:
![]()
![]()
![]()
同理有:
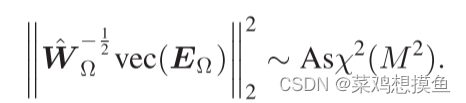
同样有LRMR问题:
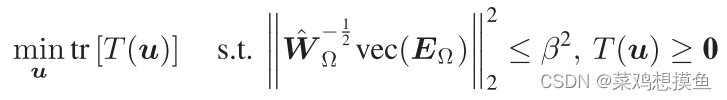
有限快拍效应
无论是SLA或ULA(可认为是SLA的特例),最后得到的优化问题都可以重新表述为:
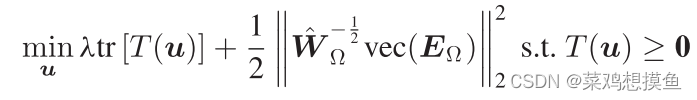
(推导省略)可以得到:
T的估计误差随着快拍数的增加而减小。(诚然,这是容易经验判断的)T的真值在L(快拍数)中是统计一致的。因为DOA由T得到,同理可以说,角度的估计在L中是统计一致的。
上述优化问题可以通过CVX or SeDuMi求解。
MATLAB代码
%% TOEPLITZ COVARIANCE MATRIX RECONSTRUCTION APPROACH FOR DIRECTION-OF-ARRIVAL ESTIMATION
%% IEEE TRANSACTIONS ON VEHICULAR TECHNOLOGY, VOL. 66, NO. 9, SEPTEMBER 2017clc;
clear all;
close all;%% 稀疏阵/互质阵
M = 3;
N = 5;
L = M+N-1;
array1 = 0:M:(N-1)*M;
array2 = 0:N:(M-1)*N;
array = [array1 array2];
array = unique(array);
arraymax = max(array); %% 均匀阵
% L = 12;
% array = 0:L-1;
% arraymax = max(array);d = 0.5;
theta = [ -3 20];
K = length(theta);
A = exp(-1i*2*pi*d*array'*sind(theta));
snap = 500;t=1:snap;
f0 = 0.005;
% s = 2.*(ones(K,1)*exp(1j*2*pi*(f0*t)));%独立信源s = randn(length(theta),snap);% s = complex(rand(length(theta),1),rand(length(theta),1));
% phi = rand(1,snap) + 0.02;
% s = s*exp(-1i*2*pi*phi);
x= A*s;
snr = 0;
x = awgn (x,snr);%% x重排为xv
% xv = zeros(arraymax+1,snap);
% for ii = 0:arraymax
% count = find(ii == array);
% if count
% xv(ii+1,:) = x(count,:);
% end
% end
%
% x = xv;G = zeros(L,arraymax+1);
for ii = 0: arraymaxcount = find(ii == array);if countG(count,ii+1)=1;end
endR = x*x'/snap;
vecR = vec(R);
MM = arraymax+1;W = kron(R.',R)/snap;
WW = (W)^(-0.5);%%%%%利用CVX工具箱求解凸优化问题%%%%%
mu = 1;
cvx_begin sdp quiet
% cvx_precision high
cvx_solver sdpt3variable T(MM,MM) hermitian toeplitz semidefinite minimize( 0.5*sum_square_abs( WW *vec(R-G*T*G')) + mu * trace(T) ) %目标函数cvx_endderad = pi/180;
[EV,Dv] = eig(T);%特征值分解
DD = diag(Dv);%将特征值变为向量形式
[DD,I] = sort(DD);%从小到大
DD = fliplr(DD');%翻转函数,从大到小
EV = fliplr(EV(:,I));
En = EV(:,K+1:end);%噪声子空间
dm_ss = 0:arraymax;
dm_ss = dm_ss*d;
for ii = 1:2001angle(ii) = (ii-1001)*90/1000;phim = derad*angle(ii);a = exp(-1j*2*pi*dm_ss*sin(phim) ).';Pmusic(ii) = 1/(a'*En*En'*a);
end
Pmusic = abs(Pmusic);
Pmax = max(Pmusic);
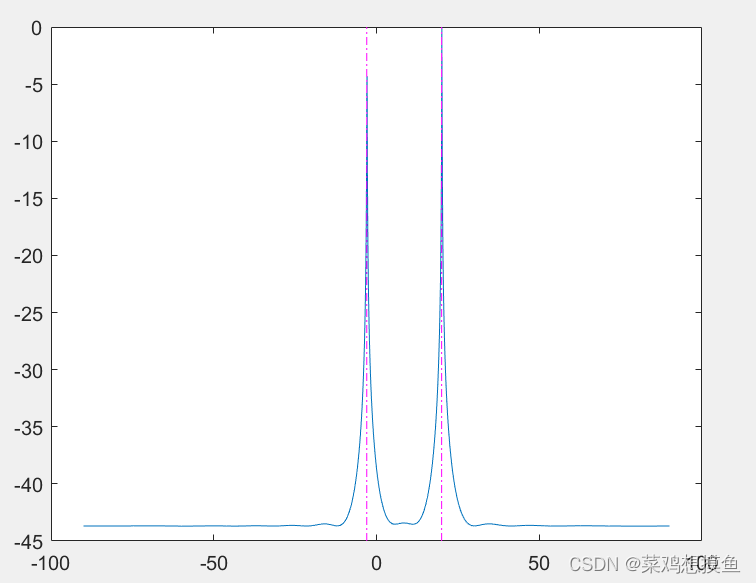
Pmusic_db = 10*log10(Pmusic/Pmax);plot(angle,Pmusic_db);
hold on;
plot([theta(1),theta(1)],ylim,'m-.');
plot([theta(2),theta(2)],ylim,'m-.');仿真结果:-3与20
注意:代码中有几点不足。
一是没有计算噪声能量,因此对误差分量的计算是不完整的。有兴趣的朋友可以自行添加。
二是得到谱峰后没有提取角度,同样没有计算RMSE。为方便,可用root-MUSIC算法直接完成角度输出(方便进行RMSE的计算)。
三是对相关信号处理效果一般,代码中也没有写空间平滑算法。同样,有兴趣的朋友可以一起讨论。
在论文中,作者通过另外两种方法进行实现,提高了速度和精度。
对偶优化
暂时先放着,再看看
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!