KF-GINS源码阅读

原始 Markdown文档、Visio流程图、XMind思维导图见：https://github.com/LiZhengXiao99/Navigation-Learning

文章目录

• • 一、KF-GINS 简介
  • • 1、程序概述
    • 2、相关资料
    • 3、文件结构
    • 4、第三方库
  • 二、编译、调试
  • 三、类型定义
  • • 1、核心类：GIEngine
    • 2、文件读写类型
    • 3、配置选项类：GINSOptions
    • 4、大地参数计算静态类：Earth
    • 5、角度弧度转换静态类：Angle
  • 四、程序执行流程
  • • 1、函数调用关系
    • 2、重点函数
    • 3、主函数
    • 4、配置文件读取
    • 5、数据文件读取
    • 6、newImuProcess()：松组合
  • 六、Earth 类：地球参数和坐标转换
  • • 1、gravity()：正常重力计算
    • 2、meridianPrimeVerticalRadius()：计算子午圈半径 RM、卯酉圈半径 RN
    • 3、RN()：计算卯酉圈主半径 RN
    • 4、cne()：n系(导航坐标系)到e系(地心地固坐标系)转换矩阵
    • 5、qne()：计算n系(北东地)到e系(ECEF)转换四元数
    • 6、blh()：从n系到e系转换四元数得到纬度和经度
    • 7、blh2ecef()：大地坐标(纬度、经度和高程)转地心地固坐标
    • 7、ecef2blh()：地心地固坐标转大地坐标
    • 8、DRi()：n系相对位置转大地坐标相对位置
    • 9、DR()：大地坐标相对位置转n系相对位置
    • 10、local2global()：局部坐标(在origin处展开)转大地坐标
    • 11、global2local()：大地坐标转局部坐标(在origin处展开)
    • 12、iewe()：地球自转角速度投影到e系
    • 13、iewn()：地球自转角速度投影到n系
    • 14、enwn()：n系相对于e系转动角速度投影到n系
  • 七、捷联惯导更新：insPropagation()
  • • 1、insPropagation()：捷联惯导递推
    • 2、imuCompensate()：IMU数据误差补偿
    • 3、insMech()：IMU 状态更新（机械编排）
    • 4、velUpdate()：速度更新
    • 5、posUpdate()：位置更新
    • 6、attUpdate()：姿态更新
    • 7、噪声传播
  • 八、GNSS 量测更新、系统状态反馈
  • • 1、gnssUpdate()：GNSS 量测更新
    • 2、EKFUpdate()：EKF 更新协方差和误差状态
    • 3、stateFeedback()：状态反馈
  • 九、KF-GINS常见问题
  • • KF-GINS能够达到怎么样的定位精度？
    • 初始导航状态和初始导航状态标准差如何给定？
    • IMU数据输入到程序之前，需要扣除重力加速度吗？
    • INS机械编排中旋转效应等补偿项，对于低端IMU是否需要补偿？
    • 组合导航中GNSS信号丢失期间进行纯惯导解算，这时IMU误差项可以补偿吗？
    • IMU数据，如何从速率形式转到增量形式？
    • IMU零偏和比例因子建模时相关时间如何给定？
    • GNSS/INS组合导航中是否需要考虑惯性系和车体系的转换？
    • 初始化拓展
    • 观测信息拓展
    • 状态信息拓展

一、KF-GINS 简介

1、程序概述

KF-GINS 是武大 i2Nav 实验室开源的一套松组合导航程序；可以读取 IMU 数据文件、GNSS 结果文件，进行松组合解算，计算位置、速度、姿态、陀螺仪零偏、加速度计零偏、陀螺仪比例、加速度计比力，共 21 维状态向量。代码量小，有详细的文档、注释和讲解，代码结构很好理解，有一些可以学习的工程技巧。

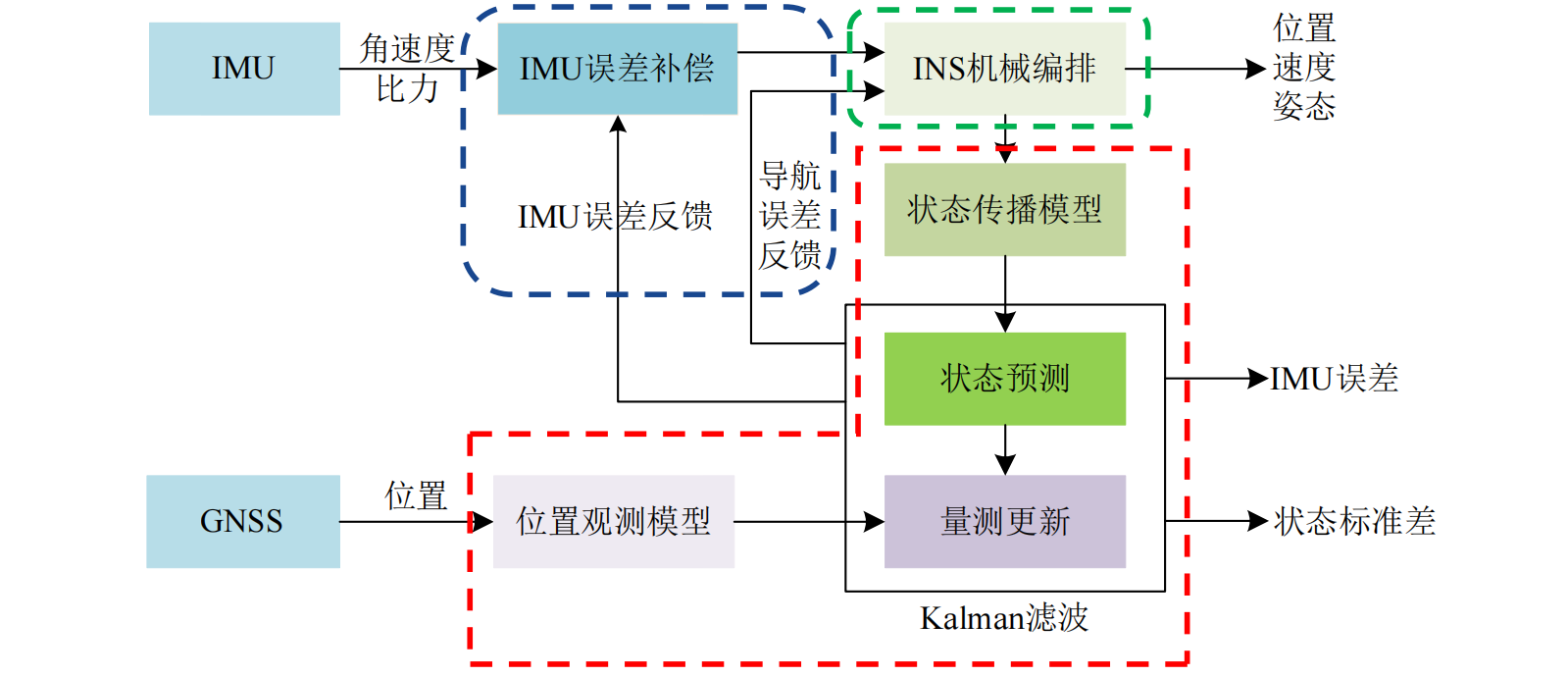
2、相关资料

• 项目开源地址：https://github.com/i2Nav-WHU
• i2NAV组合导航讲义、数据集：http://www.i2nav.cn/index/newList_zw?newskind_id=13a8654e060c40c69e5f3d4c13069078
• 介绍视频：https://www.bilibili.com/video/BV1Zs4y1B7m2/

3、文件结构

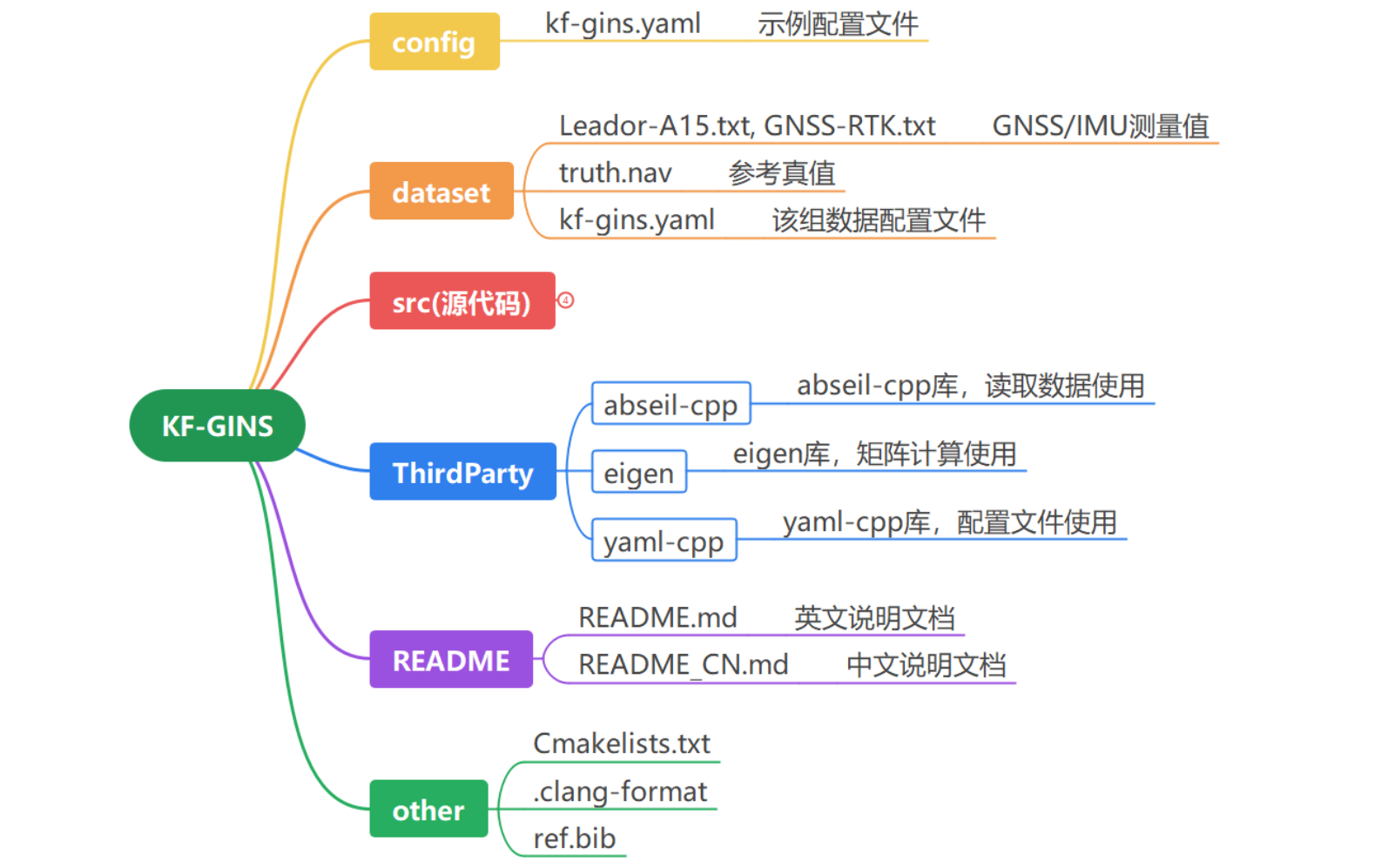
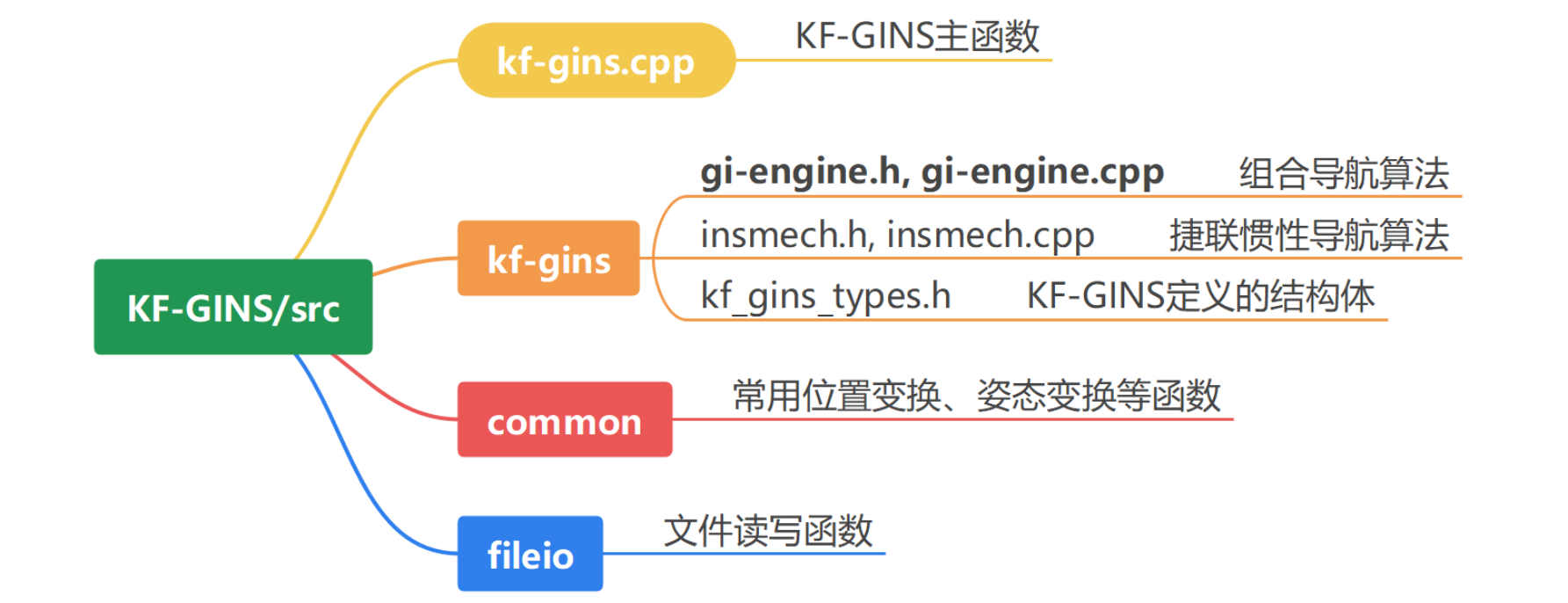
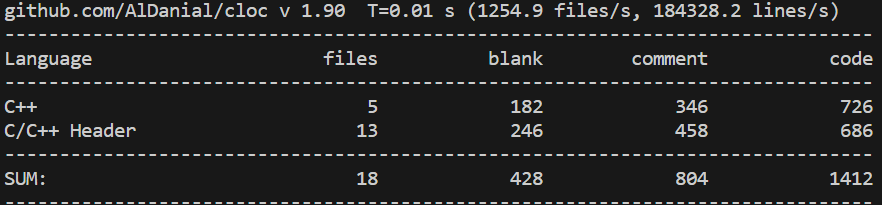
用 cloc 对 src 目录进行统计，结果如下。可以看出代码量很小，只有1412行，注释很详细，足有804行。

4、第三方库

• abseil-cpp：Google的开源C++库，提供了一系列实用的工具和功能，例如字符串处理、时间处理、错误处理、日志记录等。
• eigen：用于线性代数、矩阵和向量操作、数值计算和转换。
• yaml-cpp：YAML解析器和生成器库。

无需自己配置，作者把它们放到 ThirdParty 文件夹，并在 CMakeLists 文件中引入了：

# Eigen3
include_directories(ThirdParty/eigen-3.3.9)# yaml-cpp-0.7.0
add_subdirectory(ThirdParty/yaml-cpp-0.7.0)
target_link_libraries(${PROJECT_NAME} yaml-cpp)# abseil
set(ABSL_PROPAGATE_CXX_STD true)
add_subdirectory(ThirdParty/abseil-cpp-20220623.1)
target_link_libraries(${PROJECT_NAME}absl::stringsabsl::str_formatabsl::time)

二、编译、调试

基于 WSL + VScode 编译非常容易，用的几个库都直接放到 ThirdParty 文件夹，并在 CMakeLists 文件中引入了，不用我们再配置。如果已经配置好基础的 C++ 环境（cmake、gcc、gdb），把项目 clone 下来之后，选 KF-GINS 目录的 CMakeLists.txt 作为构建目标直接就能构建、编译成功，调试时能停在 main 函数开头设的断点。

launch.json 中作者已经设置命令行参数为配置文件路径，我们只要改好 config 路径下 kf-gins.yaml 配置文件中的 几个文件路径（imupath、gnsspath、outputpath）和解算时间（starttime、endtime），就可以跑通示例数据了。

三、类型定义

1、核心类：GIEngine

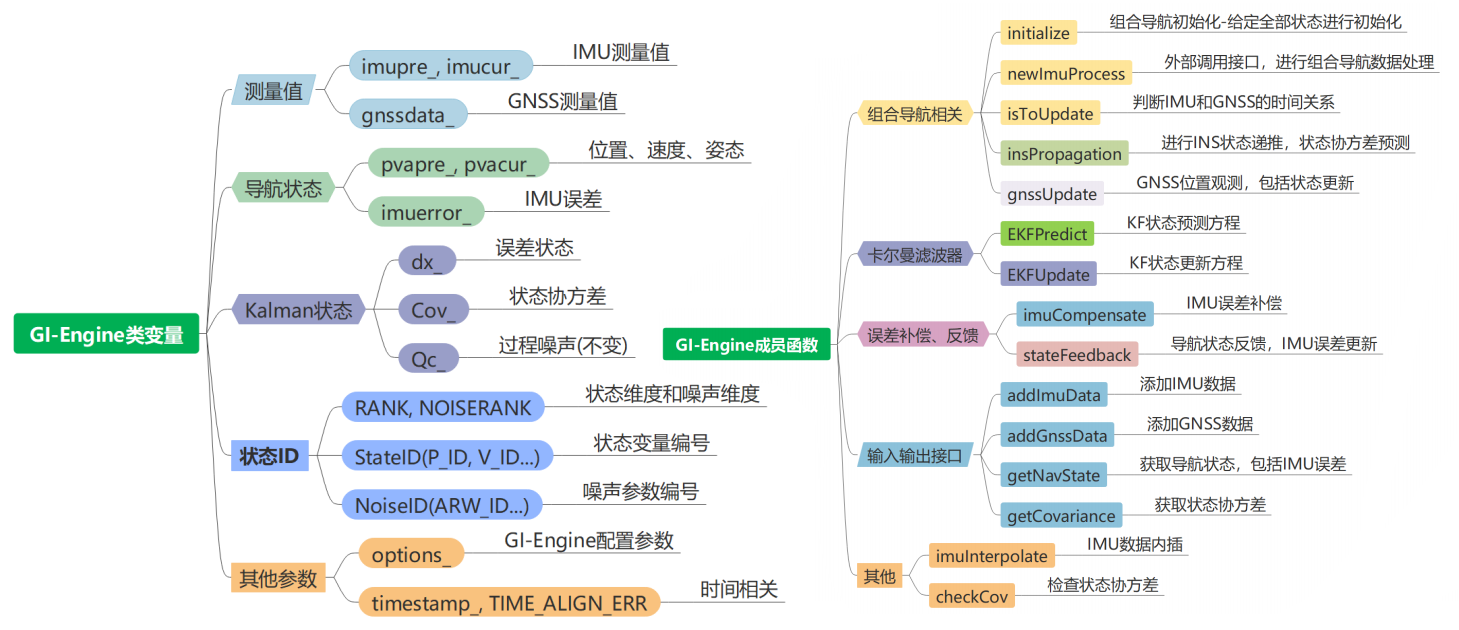
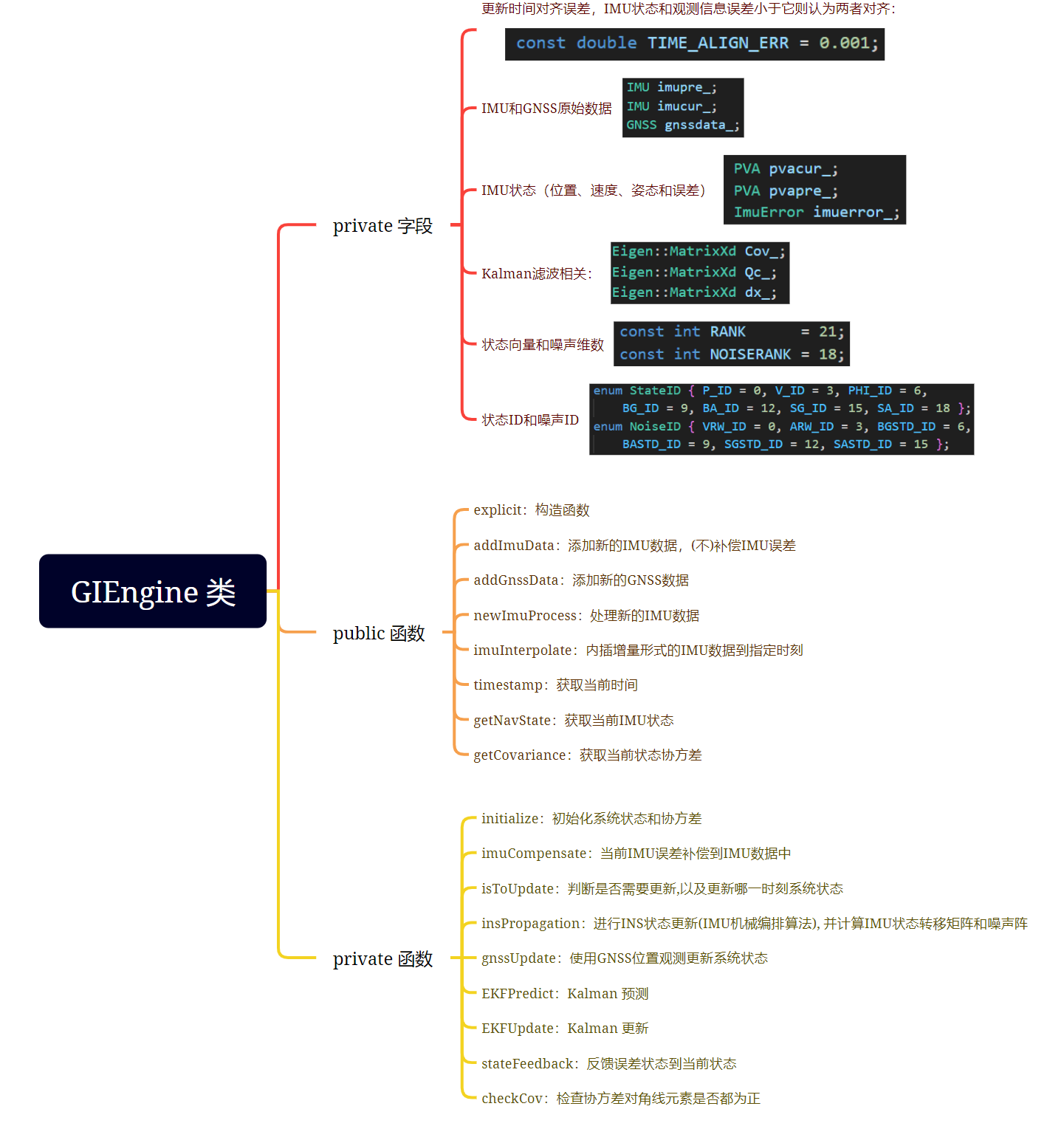
2、文件读写类型

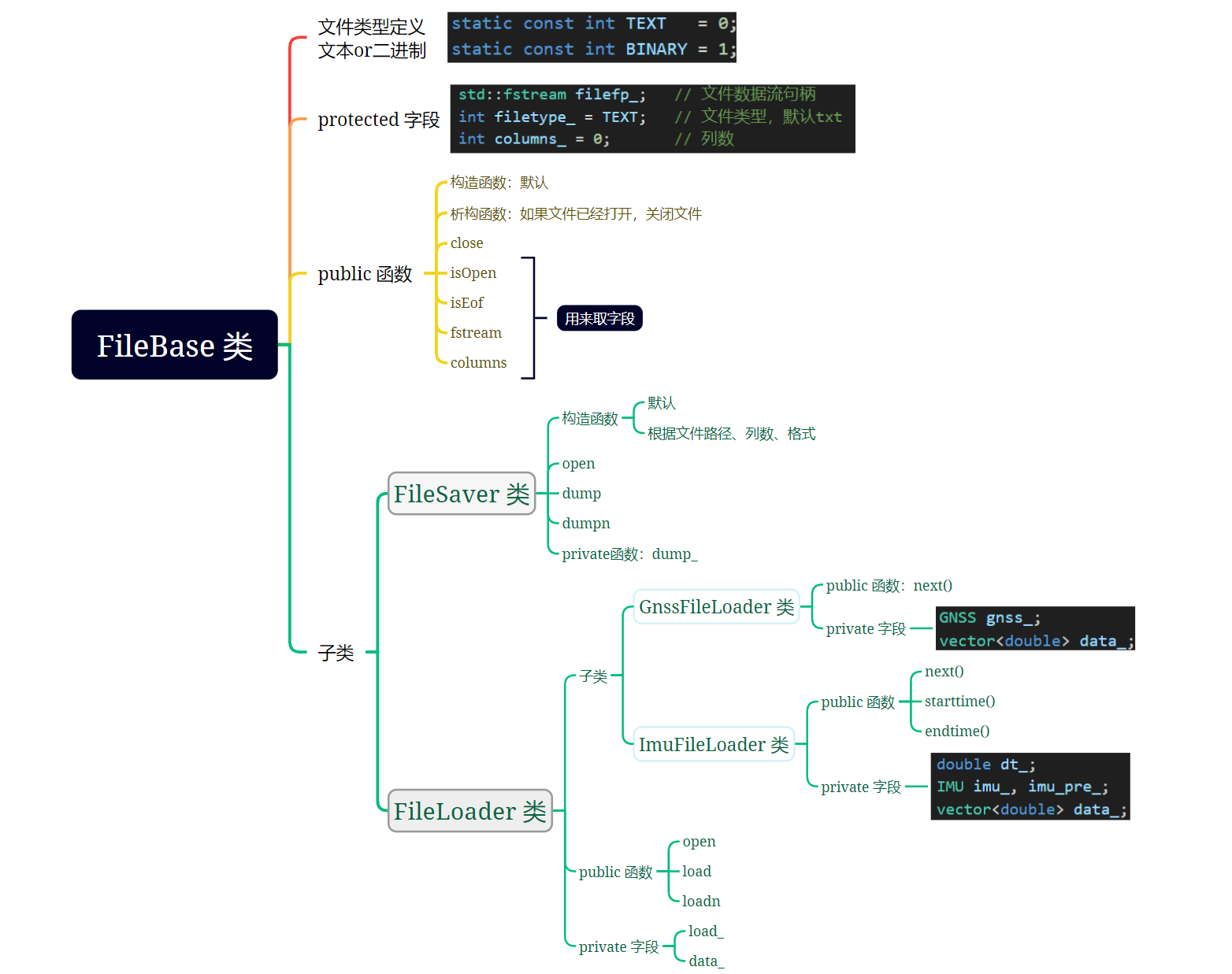
3、配置选项类：GINSOptions

4、大地参数计算静态类：Earth

5、角度弧度转换静态类：Angle

四、程序执行流程

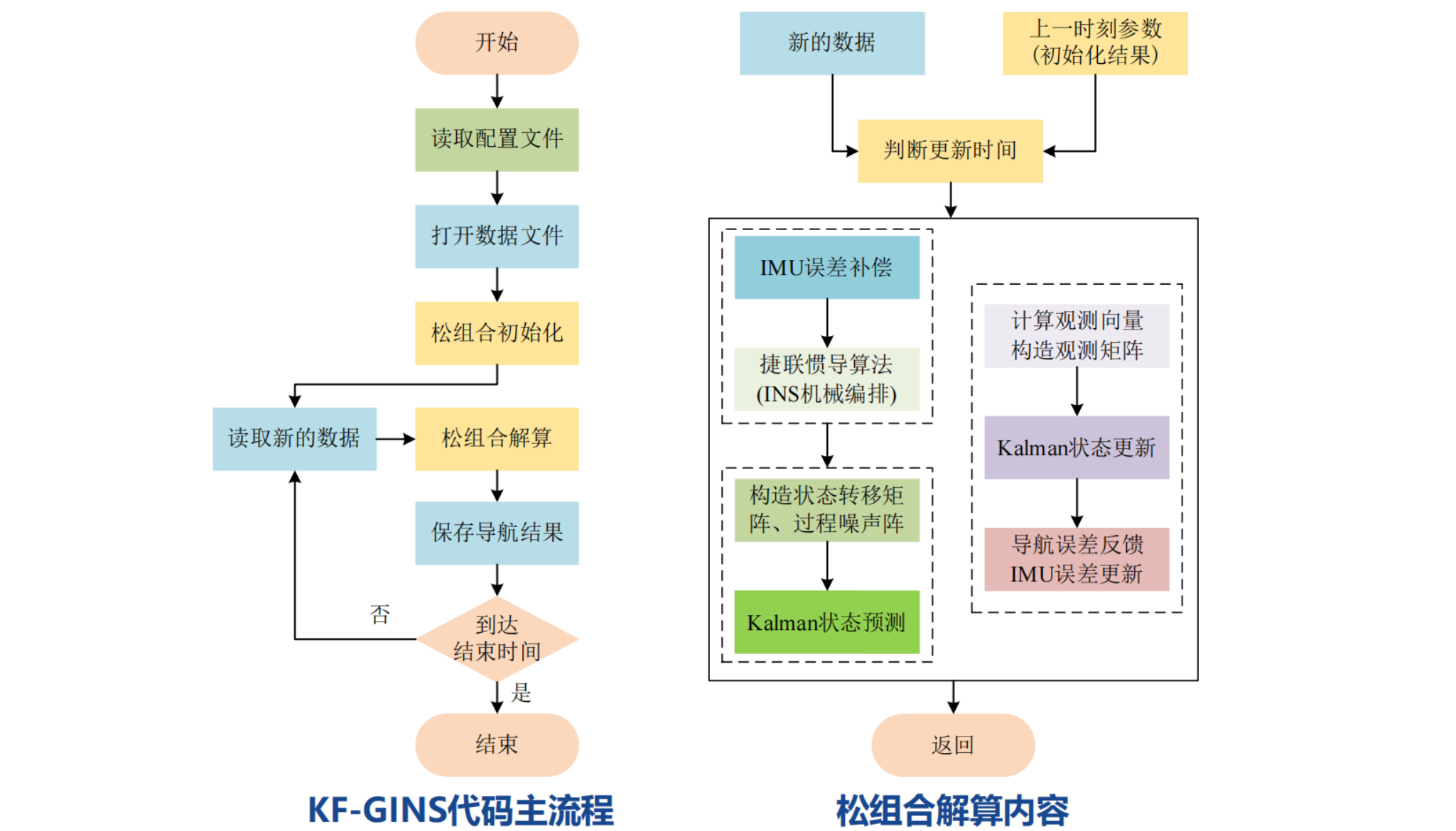
1、函数调用关系

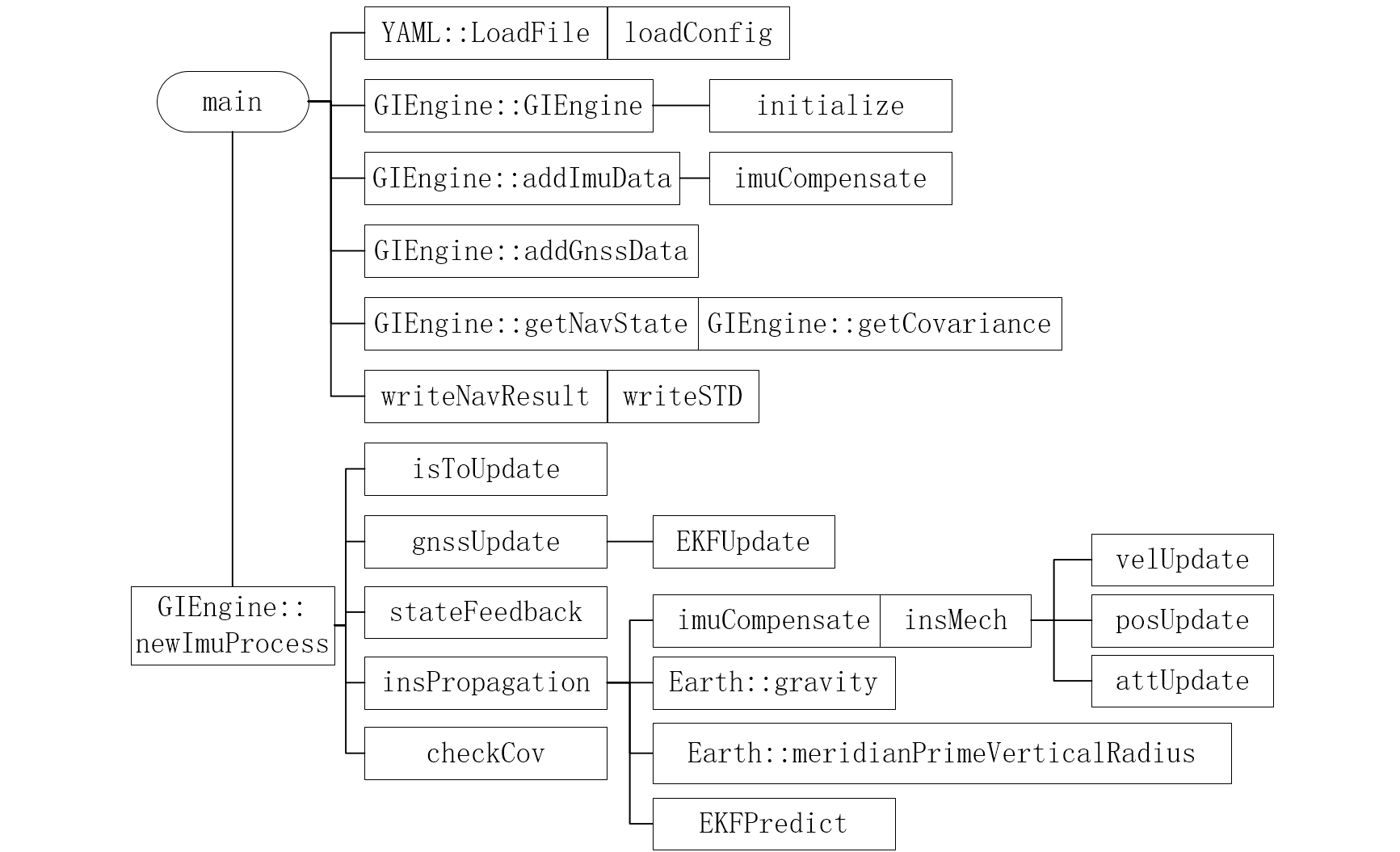
2、重点函数

• newImuProcess() 是松组合的核心函数。
• isToUpdate() 中根据当前 IMU 和 GNSS 时间戳关系，判断要不要进行 GNSS 量测更新。
• imuCompensate() 中进行 IMU 校正，即减去零偏、除以比例。
• insPropagation() 中实现捷联惯导 PVA 和噪声递推、构建 F 矩阵。
• insMech() 中 IMU 机械编排，依次进行速度更新、位置更新、姿态更新。
• gnssUpdate() 中进行 GNSS 量测更新，实现杆臂补偿。
• stateFeedback() GNSS 量测更新后，状态向量误差反馈。

3、主函数

首先判断命令行参数，如果不为 2（可执行程序名算第一个参数 argv[0]）即没传入配置文件路径，输出提示并退出程序：

if (argc != 2) {std::cout << "usage: KF-GINS kf-gins.yaml" << std::endl;return -1;
}

创建 t1、t2、t3 用于计时：

long t1,t2,t3; // 用于计时
t1=clock();
std::cout << std::endl << "KF-GINS: An EKF-Based GNSS/INS Integrated Navigation System" << std::endl << std::endl;
auto ts = absl::Now();

读取配置文件：

// 加载配置文件
// load configuration file
YAML::Node config;
try {config = YAML::LoadFile(argv[1]);
} catch (YAML::Exception &exception) {std::cout << "Failed to read configuration file. Please check the path and format of the configuration file!"<< std::endl;return -1;
}// 读取配置参数到GINSOptioins中，并构造GIEngine
// load configuration parameters to GINSOptioins
GINSOptions options;
if (!loadConfig(config, options)) {std::cout << "Error occurs in the configuration file!" << std::endl;return -1;
}// 读取文件路径配置
// load filepath configuration
std::string imupath, gnsspath, outputpath;
try {imupath    = config["imupath"].as<std::string>();gnsspath   = config["gnsspath"].as<std::string>();outputpath = config["outputpath"].as<std::string>();
} catch (YAML::Exception &exception) {std::cout << "Failed when loading configuration. Please check the file path and output path!" << std::endl;return -1;
}// imu数据配置，数据处理区间
// imudata configuration， data processing interval
int imudatalen, imudatarate;
double starttime, endtime;
try {imudatalen  = config["imudatalen"].as<int>();imudatarate = config["imudatarate"].as<int>();starttime   = config["starttime"].as<double>();endtime     = config["endtime"].as<double>();
} catch (YAML::Exception &exception) {std::cout << "Failed when loading configuration. Please check the data length, data rate, and the process time!"<< std::endl;return -1;
}

根据读进来的配置，构造解算用到的几个对象：

• 文件读取对象：gnssfile、imufile
• 松组合解算核心类：giengine
• 构造输出文件对象：navfile、imuerrfile、stdfile

// 加载 GNSS 文件和 IMU 文件
// load GNSS file and IMU file
GnssFileLoader gnssfile(gnsspath);
ImuFileLoader imufile(imupath, imudatalen, imudatarate);t2 =clock();// 构造GIEngine
// Construct GIEngine
GIEngine giengine(options);// 构造输出文件
// construct output file
// navfile: gnssweek(1) + time(1) + pos(3) + vel(3) + euler angle(3) = 11
// imuerrfile: time(1) + gyrbias(3) + accbias(3) + gyrscale(3) + accscale(3) = 13
// stdfile: time(1) + pva_std(9) + imubias_std(6) + imuscale_std(6) = 22
int nav_columns = 11, imuerr_columns = 13, std_columns = 22;
FileSaver navfile(outputpath + "/KF_GINS_Navresult.nav", nav_columns, FileSaver::TEXT);
FileSaver imuerrfile(outputpath + "/KF_GINS_IMU_ERR.txt", imuerr_columns, FileSaver::TEXT);
FileSaver stdfile(outputpath + "/KF_GINS_STD.txt", std_columns, FileSaver::TEXT);// 检查文件是否正确打开
// check if these files are all opened
if (!gnssfile.isOpen() || !imufile.isOpen() || !navfile.isOpen() || !imuerrfile.isOpen() || !stdfile.isOpen()) {std::cout << "Failed to open data file!" << std::endl;return -1;
}

检查处理起止时间是否合理：

if (endtime < 0) {endtime = imufile.endtime();
}
if (endtime > 604800 || starttime < imufile.starttime() || starttime > endtime) {std::cout << "Process time ERROR!" << std::endl;return -1;
}

循环调用 imufile.next()、gnssfile.next() 读取 IMU、GNSS 数据，直到时间戳在解算时间范围内。循环结束后 imu_cur、gnss 分别存解算时间内第一个IMU、GNSS量测，且文件指针指向的位置也到达解算时间内数据的开头：

IMU imu_cur;
do {imu_cur = imufile.next();
} while (imu_cur.time < starttime);GNSS gnss;
do {gnss = gnssfile.next();
} while (gnss.time <= starttime);

调用 addImuData()、addGnssData() 将刚刚读取到解算时间范围内第一个 IMU、GNSS 数据加入 giengine，并对 IMU 数据进行误差补偿，减去零偏、除以加上单位阵后的比例：

// 添加IMU数据到GIEngine中，补偿IMU误差
// add imudata to GIEngine and compensate IMU error
giengine.addImuData(imu_cur, true);// 添加GNSS数据到GIEngine
// add gnssdata to GIEngine
giengine.addGnssData(gnss);

定义变量，用于保存处理结果、显示处理进度：

// 用于保存处理结果
// used to save processing results
double timestamp;
NavState navstate;
Eigen::MatrixXd cov;// 用于显示处理进程
// used to display processing progress
int percent = 0, lastpercent = 0;
double interval = endtime - starttime;

接下来是一个大 while 死循环，每次循环都会读取一个 IMU 数据，只有当前 IMU 状态时间新于 GNSS 时间时，才会读取 GNSS 数据：

// 当前IMU状态时间新于GNSS时间时，读取并添加新的GNSS数据到GIEngine
// load new gnssdata when current state time is newer than GNSS time and add it to GIEngine
if (gnss.time < imu_cur.time && !gnssfile.isEof()) {gnss = gnssfile.next();giengine.addGnssData(gnss);
}// 读取并添加新的IMU数据到GIEngine
// load new imudata and add it to GIEngine
imu_cur = imufile.next();
if (imu_cur.time > endtime || imufile.isEof()) {break;
}
giengine.addImuData(imu_cur);

调用 newImuProcess() 根据当前 IMU、GNSS 数据进行解算，下面会重点介绍：

giengine.newImuProcess();

解算之后，获取当前时间，IMU状态和协方差、保存并输出处理结果，输出结果的时间戳与 IMU 时间戳一致：

// 获取当前时间，IMU状态和协方差
// get current timestamp, navigation state and covariance
timestamp = giengine.timestamp();
navstate  = giengine.getNavState();
cov       = giengine.getCovariance();// 保存处理结果
// save processing results
writeNavResult(timestamp, navstate, navfile, imuerrfile);
writeSTD(timestamp, cov, stdfile);

显示处理进度：

percent = int((imu_cur.time - starttime) / interval * 100);if (percent - lastpercent >= 1) {std::cout << " - Processing: " << std::setw(3) << percent << "%\r" << std::flush;lastpercent = percent;
}

循环处理完成之后，关闭打开的文件、输出结束信息、return 0 退出程序：

// 关闭打开的文件
// close opened file
imufile.close();
gnssfile.close();
navfile.close();
imuerrfile.close();
stdfile.close();// 处理完毕
// process finish
auto te = absl::Now();
std::cout << std::endl << std::endl << "KF-GINS Process Finish! ";
std::cout << "From " << starttime << " s to " << endtime << " s, total " << interval << " s!" << std::endl;
std::cout << "Cost " << absl::ToDoubleSeconds(te - ts) << " s in total" << std::endl;return 0;

4、配置文件读取

KF-GINS 使用 YMAL 格式的配置文件，通过配置文件可以设置数据文件路径、处理时间段、初始PVA、初始比例零偏、杆臂等。KF-GINS 的配置都是键值对形式的： 键 :值，设置的时候改后面的值即可。程序执行的时候要把配置文件路径作为命令行参数。下面简单介绍读取流程：

在主函数中先调用 yaml-cpp 的接口 YAML::LoadFile() 通过 YMAL 配置文件路径，将配置导入为 YMAL 节点 config：

YAML::Node config;
try {config = YAML::LoadFile(argv[1]);
} catch (YAML::Exception &exception) {std::cout << "Failed to read configuration file. Please check the path and format of the configuration file!"<< std::endl;return -1;
}

然后调用 loadConfig() 从 YMAL 根节点 config 读取配置参数到 GINSOptions 类型对象 options 中：

GINSOptions options;
if (!loadConfig(config, options)) {std::cout << "Error occurs in the configuration file!" << std::endl;return -1;
}

需要注意 loadConfig() 并没有把所有配置信息都读进来，它读取的只是取初始位置、IMU零偏、比例和对应的标准差；大部分参数都是三维的，读取的时候先存成 vector 然后进行量纲、单位转换，再存到 options 对应的 vector3d 类型字段中。以初始 PVA 为例：

// 读取初始位置(纬度 经度 高程)、(北向速度 东向速度 垂向速度)、姿态(欧拉角，ZYX旋转顺序, 横滚角、俯仰角、航向角)
// load initial position(latitude longitude altitude)
//              velocity(speeds in the directions of north, east and down)
//              attitude(euler angle, ZYX, roll, pitch and yaw)
std::vector<double> vec1, vec2, vec3, vec4, vec5, vec6;
try {vec1 = config["initpos"].as<std::vector<double>>();vec2 = config["initvel"].as<std::vector<double>>();vec3 = config["initatt"].as<std::vector<double>>();
} catch (YAML::Exception &exception) {std::cout << "Failed when loading configuration. Please check initial position, velocity, and attitude!"<< std::endl;return false;
}
for (int i = 0; i < 3; i++) {   // 单位转换options.initstate.pos[i]   = vec1[i] * D2R;options.initstate.vel[i]   = vec2[i];options.initstate.euler[i] = vec3[i] * D2R;
}
options.initstate.pos[2] *= R2D;    // 高程不用转

文件路径和 IMU 处理配置是在主函数中读取：

// 读取文件路径配置
// load filepath configuration
std::string imupath, gnsspath, outputpath;
try {imupath    = config["imupath"].as<std::string>();gnsspath   = config["gnsspath"].as<std::string>();outputpath = config["outputpath"].as<std::string>();
} catch (YAML::Exception &exception) {std::cout << "Failed when loading configuration. Please check the file path and output path!" << std::endl;return -1;
}// imu数据配置，数据处理区间
// imudata configuration， data processing interval
int imudatalen, imudatarate;
double starttime, endtime;
try {imudatalen  = config["imudatalen"].as<int>();imudatarate = config["imudatarate"].as<int>();starttime   = config["starttime"].as<double>();endtime     = config["endtime"].as<double>();
} catch (YAML::Exception &exception) {std::cout << "Failed when loading configuration. Please check the data length, data rate, and the process time!"<< std::endl;return -1;
}

5、数据文件读取

KF-GINS 中没有一次性把整个文件都读进来；而是先打开文件，获取文件描述符；然后计算一点，读一点，模仿实时解算。

在主函数中先构造 GnssFileLoader、ImuFileLoader 类的对象 gnssfile、imufile：

GnssFileLoader gnssfile(gnsspath);
ImuFileLoader imufile(imupath, imudatalen, imudatarate);

构造函数中调用 open() 函数，将文件打开，获得文件指针，并记录下文件列数和 IMU 采样间隔。

explicit GnssFileLoader(const string &filename, int columns = 7) {open(filename, columns, FileLoader::TEXT);
}

ImuFileLoader(const string &filename, int columns, int rate = 200) {open(filename, columns, FileLoader::TEXT);dt_ = 1.0 / (double) rate;imu_.time = 0;
}

bool FileLoader::open(const string &filename, int columns, int filetype) {auto type = filetype == TEXT ? std::ios_base::in : (std::ios_base::in | std::ios_base::binary);filefp_.open(filename, type);columns_  = columns;filetype_ = filetype;return isOpen();
}

调用 imufile.next()、gnssfile.next()，读取一个数据。

在主文件中，先循环调用 imufile.next()、gnssfile.next() 读取 IMU、GNSS 数据，直到时间戳在解算时间范围内。循环结束后 imu_cur、gnss 分别存解算时间内第一个 IMU、GNSS 量测，且文件指针指向的位置也到达解算时间内数据的开头：

IMU imu_cur;
do {imu_cur = imufile.next();
} while (imu_cur.time < starttime);GNSS gnss;
do {gnss = gnssfile.next();
} while (gnss.time <= starttime);

之后每次循环解算，都会读取一个 IMU 数据，只有当前 IMU 状态时间新于 GNSS 时间时，才会读取 GNSS 数据：

while (true) {// 当前IMU状态时间新于GNSS时间时，读取并添加新的GNSS数据到GIEngine// load new gnssdata when current state time is newer than GNSS time and add it to GIEngineif (gnss.time < imu_cur.time && !gnssfile.isEof()) {gnss = gnssfile.next();giengine.addGnssData(gnss);}// 读取并添加新的IMU数据到GIEngine// load new imudata and add it to GIEngineimu_cur = imufile.next();if (imu_cur.time > endtime || imufile.isEof()) {break;}

6、newImuProcess()：松组合

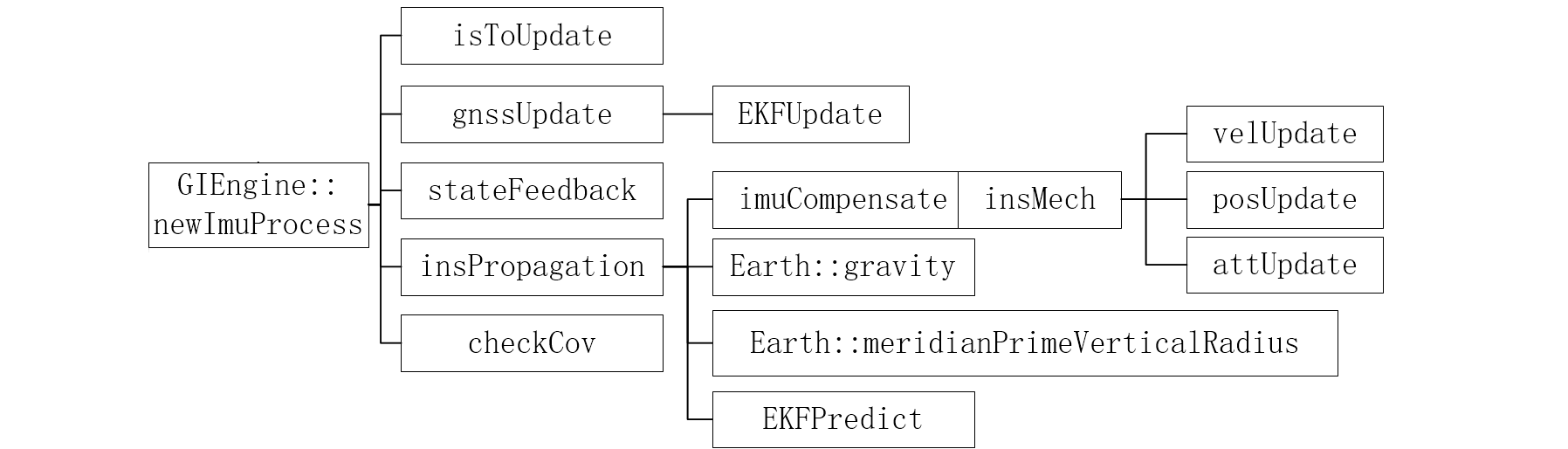
这个函数是松组合解算的入口，IMU 量测的频率远远大于 GNSS 量测；所以用 IMU 为基准，得到的系统状态向量和协方差阵是当前 IMU 时间的，每次调用这个函数都会有新 IMU 量测。函数的计算基于当前时刻 IMU 量测和上一时刻 IMU 量测，如果两次量测之间没有 GNSS 数据，就只是进行捷联惯导递推，将系统状态和噪声递推到当前时刻；如果两次量测间有 GNSS 数据，就先捷联惯导递推到 GNSS 时刻，在 GNSS 时刻进行量测更新、误差反馈，最后再捷联惯导递推到当前时刻。

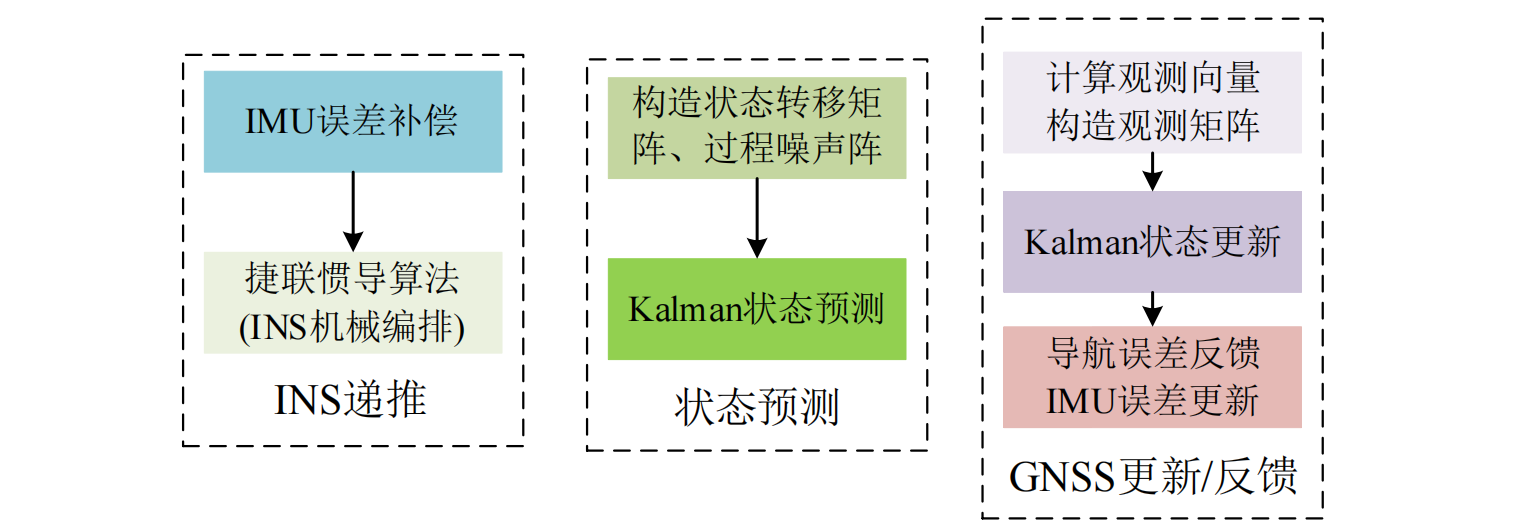
首先将当前 IMU 时间作为系统当前状态时间，也就是说这个函数执行完之后，得到的系统状态向量和协方差阵是当前 IMU 时间的：

timestamp_ = imucur_.time;

如果GNSS有效，则将量测更新时间设置为 GNSS 时间：

double updatetime = gnssdata_.isvalid ? gnssdata_.time : -1;

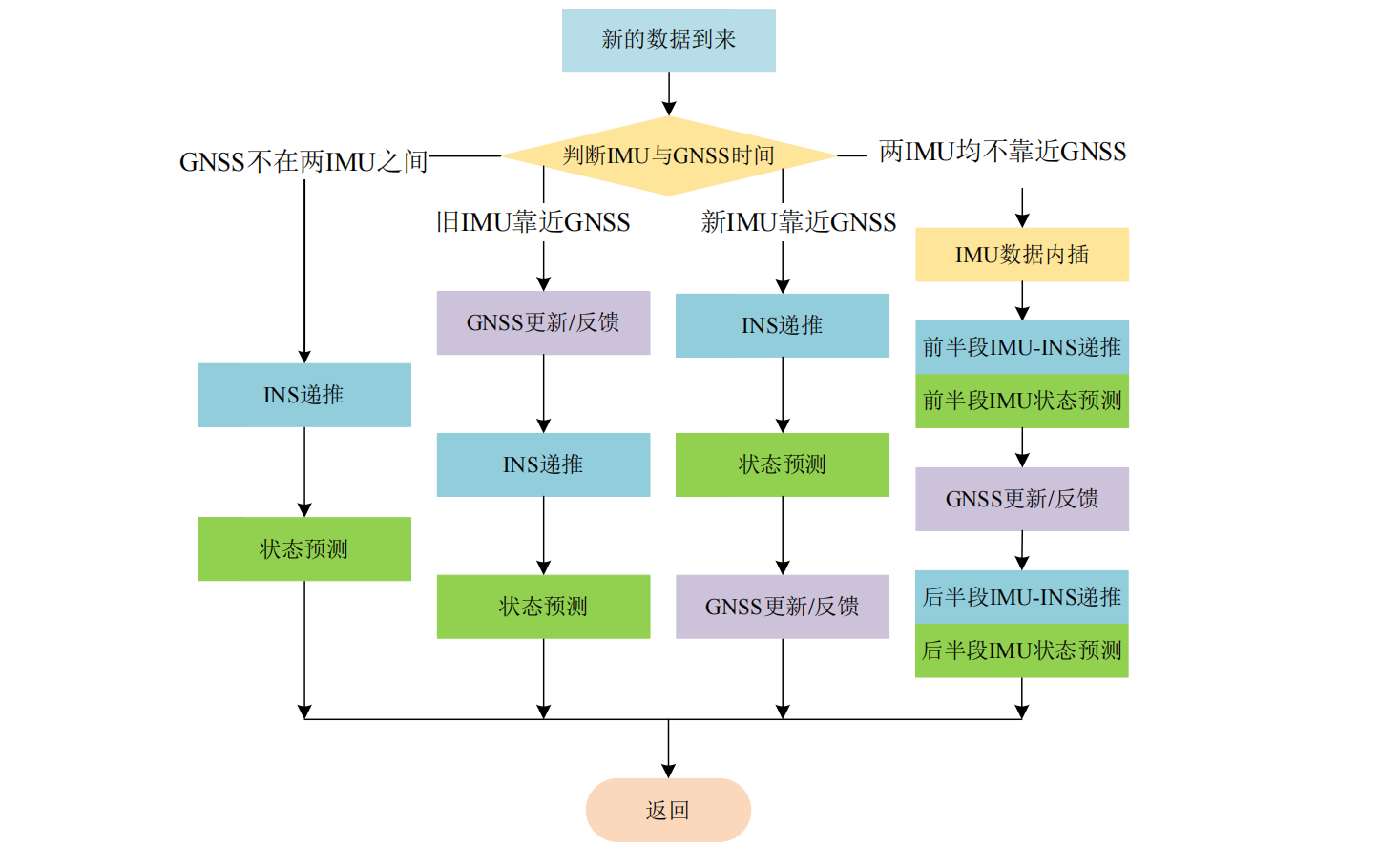
先调用 isToUpdate()，根据当前 GNSS 与当前和先前两 IMU 量测的时间关系，判断是否需要进行 GNSS 更新，有四种情况，分别返回不同的值：

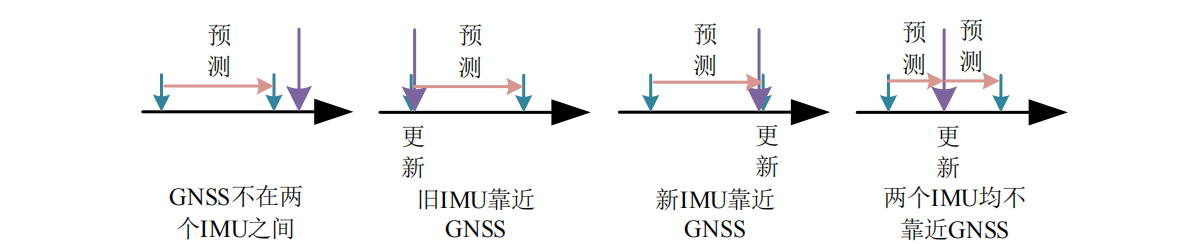
int GIEngine::isToUpdate(double imutime1, double imutime2, double updatetime) const {if (abs(imutime1 - updatetime) < TIME_ALIGN_ERR) {// 更新时间靠近imutime1// updatetime is near to imutime1return 1;} else if (abs(imutime2 - updatetime) <= TIME_ALIGN_ERR) {// 更新时间靠近imutime2// updatetime is near to imutime2return 2;} else if (imutime1 < updatetime && updatetime < imutime2) {// 更新时间在imutime1和imutime2之间, 但不靠近任何一个// updatetime is between imutime1 and imutime2, but not near to eitherreturn 3;} else {// 更新时间不在imutimt1和imutime2之间，且不靠近任何一个// updatetime is not bewteen imutime1 and imutime2, and not near to either.return 0;}
}

根据更新时间对齐误差 TIME_ALIGN_ERR 评定是否靠近，默认为 0.001，也就是说时间差距在 1ms 内，认为是靠近的。文档和注释都用“靠近”这个词，起始与其说是“靠近”，更像是在说是“重合”。

返回 0，表示 GNSS 不在两个 IMU 之间，在当前 IMU 量测之后，那么只进行捷联惯导递推，调用 insPropagation() 根据两帧 IMU 量测将状态递推到当前 IMU 时间戳：

if (res == 0) {// 只传播导航状态// only propagate navigation stateinsPropagation(imupre_, imucur_);

返回 1，表示 GNSS 在两个 IMU 之间，更靠近前一个 IMU：

• 先调用 gnssUpdate() 进行 GNSS 量测更新；
• 再调用 stateFeedback() 进行系统状态反馈；
• 最后调用 insPropagation() 根据两帧 IMU 量测将状态递推到当前 IMU 时间戳：

} else if (res == 1) {// GNSS数据靠近上一历元，先对上一历元进行GNSS更新// gnssdata is near to the previous imudata, we should firstly do gnss updategnssUpdate(gnssdata_);stateFeedback();pvapre_ = pvacur_;insPropagation(imupre_, imucur_);

返回 2，表示 GNSS 在两个 IMU 之间，更靠近后一个 IMU：

• 先调用 insPropagation() 根据两帧 IMU 量测将状态递推到当前 IMU 时间戳；
• 再调用 gnssUpdate() 进行 GNSS 量测更新；
• 最后调用 stateFeedback() 进行系统状态反馈：

} else if (res == 2) {// GNSS数据靠近当前历元，先对当前IMU进行状态传播// gnssdata is near current imudata, we should firstly propagate navigation stateinsPropagation(imupre_, imucur_);gnssUpdate(gnssdata_);stateFeedback();

返回 3，表示 GNSS 在两个 IMU 之间，不靠近任何一个：

• 先调用 imuInterpolate() 根据两帧 IMU 量测插值到 GNSS 时间戳，得到 GNSS 时刻 IMU 量测值 midimu；
• 调用 insPropagation 根据前一个 IMU 和 midimu 将状态递推到当前 GNSS 时间戳；
• 再调用 gnssUpdate() 进行 GNSS 量测更新，调用 stateFeedback() 进行系统状态反馈；
• 最后再调用一次 insPropagation() 根据 midimu 和当前时刻 IMU 量测将状态递推到当前 IMU 时间戳：

} else {// GNSS数据在两个IMU数据之间(不靠近任何一个), 将当前IMU内插到整秒时刻// gnssdata is between the two imudata, we interpolate current imudata to gnss timeIMU midimu;imuInterpolate(imupre_, imucur_, updatetime, midimu);// 对前一半IMU进行状态传播// propagate navigation state for the first half imudatainsPropagation(imupre_, midimu);// 整秒时刻进行GNSS更新，并反馈系统状态// do GNSS position update at the whole second and feedback system statesgnssUpdate(gnssdata_);stateFeedback();// 对后一半IMU进行状态传播// propagate navigation state for the second half imudatapvapre_ = pvacur_;insPropagation(midimu, imucur_);
}

几种情况可总结如下图：

处理完之后调用 checkCov() 检查协方差对角线元素是否都为正，更新上一时刻的状态和 IMU 数据：

// 检查协方差对角线元素是否都为正
// check diagonal elements of current covariance matrix
checkCov();
// 更新上一时刻的状态和IMU数据
// update system state and imudata at the previous epoch
pvapre_ = pvacur_;
imupre_ = imucur_;

六、Earth 类：地球参数和坐标转换

Earth 类里都是静态函数，使用的时候直接类名::成员函数()，文件的开头定义了一些椭球参数：

/* WGS84椭球模型参数NOTE:如果使用其他椭球模型需要修改椭球参数 */
const double WGS84_WIE = 7.2921151467E-5;       /* 地球自转角速度*/
const double WGS84_F   = 0.0033528106647474805; /* 扁率 */
const double WGS84_RA  = 6378137.0000000000;    /* 长半轴a */
const double WGS84_RB  = 6356752.3142451793;    /* 短半轴b */
const double WGS84_GM0 = 398600441800000.00;    /* 地球引力常数 */
const double WGS84_E1  = 0.0066943799901413156; /* 第一偏心率平方 */
const double WGS84_E2  = 0.0067394967422764341; /* 第二偏心率平方 */

1、gravity()：正常重力计算

重力是万有引力与离心力共同作用的结果，随纬度升高离心力增大但引力减小、随高程升高引力减小，共同作用下重力的计算公式如下：

g L = 9.7803267715 × ( 1 + 0.0052790414 × sin ⁡ 2 L − 0.0000232718 × sin ⁡ 2 2 L ) + h × ( 0.0000000043977311 × sin ⁡ 2 L − 0.0000030876910891 ) + 0.0000000000007211 × sin ⁡ 4 2 L g_{L}=9.7803267715 \times\left(1+0.0052790414 \times \sin ^{2} L-0.0000232718 \times \sin ^{2} 2 L\right) \\ +h\times(0.0000000043977311\times\sin ^{2} L-0.0000030876910891)+0.0000000000007211\times\sin ^{4} 2 L gL​=9.7803267715×(1+0.0052790414×sin2L−0.0000232718×sin22L)+h×(0.0000000043977311×sin2L−0.0000030876910891)+0.0000000000007211×sin42L

static double gravity(const Vector3d &blh) {double sin2 = sin(blh[0]);sin2 *= sin2;return 9.7803267715 * (1 + 0.0052790414 * sin2 + 0.0000232718 * sin2 * sin2) +blh[2] * (0.0000000043977311 * sin2 - 0.0000030876910891) + 0.0000000000007211 * blh[2] * blh[2];
}

2、meridianPrimeVerticalRadius()：计算子午圈半径 RM、卯酉圈半径 RN

返回值是 Vector2d，第一个是子午圈主曲率半径 RM、第二个是卯酉圈主半径 RN：
R M = R e ( 1 − e 2 ) ( 1 − e 2 sin ⁡ 2 L ) 3 / 2 、 R N = R e 1 − e 2 sin ⁡ 2 L R_{M}=\frac{R_{e}\left(1-e^{2}\right)}{\left(1-e^{2} \sin ^{2} L\right)^{3 / 2}}、R_{N}=\frac{R_{e}}{\sqrt{1-e^{2} \sin ^{2} L}} RM​=(1−e2sin2L)3/2Re​(1−e2)​、RN​=1−e2sin2L ​Re​​

static Eigen::Vector2d meridianPrimeVerticalRadius(double lat) {double tmp, sqrttmp;tmp = sin(lat);	tmp *= tmp;tmp     = 1 - WGS84_E1 * tmp;sqrttmp = sqrt(tmp);return {WGS84_RA * (1 - WGS84_E1) / (sqrttmp * tmp), WGS84_RA / sqrttmp};
}

3、RN()：计算卯酉圈主半径 RN

R N = R e 1 − e 2 sin ⁡ 2 L R_{N}=\frac{R_{e}}{\sqrt{1-e^{2} \sin ^{2} L}} RN​=1−e2sin2L ​Re​​

static double RN(double lat) {double sinlat = sin(lat);return WGS84_RA / sqrt(1.0 - WGS84_E1 * sinlat * sinlat);
}

4、cne()：n系(导航坐标系)到e系(地心地固坐标系)转换矩阵

C e n = [ − sin ⁡ φ 0 cos ⁡ φ 0 1 0 − cos ⁡ φ 0 − sin ⁡ φ ] [ cos ⁡ λ sin ⁡ λ 0 − sin ⁡ λ cos ⁡ λ 0 0 0 1 ] = [ − sin ⁡ φ cos ⁡ λ − sin ⁡ φ sin ⁡ λ cos ⁡ φ − sin ⁡ λ cos ⁡ λ 0 − cos ⁡ φ cos ⁡ λ − cos ⁡ φ sin ⁡ λ − sin ⁡ φ ] C_{e}^{n}=\left[\begin{array}{ccc}-\sin \varphi & 0 & \cos \varphi \\ 0 & 1 & 0 \\ -\cos \varphi & 0 & -\sin \varphi\end{array}\right]\left[\begin{array}{ccc}\cos \lambda & \sin \lambda & 0 \\ -\sin \lambda & \cos \lambda & 0 \\ 0 & 0 & 1\end{array}\right]=\\ \left[\begin{array}{ccc}-\sin \varphi \cos \lambda & -\sin \varphi \sin \lambda & \cos \varphi \\ -\sin \lambda & \cos \lambda & 0 \\ -\cos \varphi \cos \lambda & -\cos \varphi \sin \lambda & -\sin \varphi\end{array}\right] Cen​= ​−sinφ0−cosφ​010​cosφ0−sinφ​ ​ ​cosλ−sinλ0​sinλcosλ0​001​ ​= ​−sinφcosλ−sinλ−cosφcosλ​−sinφsinλcosλ−cosφsinλ​cosφ0−sinφ​ ​

static Matrix3d cne(const Vector3d &blh) {double coslon, sinlon, coslat, sinlat;sinlat = sin(blh[0]);sinlon = sin(blh[1]);coslat = cos(blh[0]);coslon = cos(blh[1]);Matrix3d dcm;dcm(0, 0) = -sinlat * coslon;dcm(0, 1) = -sinlon;dcm(0, 2) = -coslat * coslon;dcm(1, 0) = -sinlat * sinlon;dcm(1, 1) = coslon;dcm(1, 2) = -coslat * sinlon;dcm(2, 0) = coslat;dcm(2, 1) = 0;dcm(2, 2) = -sinlat;return dcm;
}

5、qne()：计算n系(北东地)到e系(ECEF)转换四元数

位置更新的时候，调用此函数根据上一时刻经纬度，得到上一时刻的 qne，然后 qee * qne * qnn 得到当前时刻的 qne，再调用下面的 blh() 得到经纬度。
q n e = [ cos ⁡ ( − π / 4 − φ / 2 ) cos ⁡ ( λ / 2 ) − sin ⁡ ( − π / 4 − φ / 2 ) sin ⁡ ( λ / 2 ) sin ⁡ ( − π / 4 − φ / 2 ) cos ⁡ ( λ / 2 ) cos ⁡ ( − π / 4 − sin ⁡ / 2 ) sin ⁡ ( λ / 2 ) ] ] \boldsymbol{q}_{n}^{e}=\left[\begin{array}{c}\cos (-\pi / 4-\varphi / 2) \cos (\lambda / 2) \\ -\sin (-\pi / 4-\varphi / 2) \sin (\lambda / 2) \\ \sin (-\pi / 4-\varphi / 2) \cos (\lambda / 2) \\ \cos (-\pi / 4-\sin / 2) \sin (\lambda / 2)]\end{array}\right] qne​= ​cos(−π/4−φ/2)cos(λ/2)−sin(−π/4−φ/2)sin(λ/2)sin(−π/4−φ/2)cos(λ/2)cos(−π/4−sin/2)sin(λ/2)]​ ​

/* n系(导航坐标系)到e系(地心地固坐标系)转换四元数 */
static Quaterniond qne(const Vector3d &blh) {Quaterniond quat;double coslon, sinlon, coslat, sinlat;coslon = cos(blh[1] * 0.5);sinlon = sin(blh[1] * 0.5);coslat = cos(-M_PI * 0.25 - blh[0] * 0.5);sinlat = sin(-M_PI * 0.25 - blh[0] * 0.5);quat.w() = coslat * coslon;quat.x() = -sinlat * sinlon;quat.y() = sinlat * coslon;quat.z() = coslat * sinlon;return quat;
}

6、blh()：从n系到e系转换四元数得到纬度和经度

位置更新的时候，通过算当前时刻 n 系到 e 系转换四元数 qne，然后调用此函数得到经纬度。

/* 从n系到e系转换四元数得到纬度和经度 */
static Vector3d blh(const Quaterniond &qne, double height) {return {-2 * atan(qne.y() / qne.w()) - M_PI * 0.5, 2 * atan2(qne.z(), qne.w()), height};
}

7、blh2ecef()：大地坐标(纬度、经度和高程)转地心地固坐标

x = ( R N + h ) cos ⁡ L cos ⁡ λ y = ( R N + h ) cos ⁡ L sin ⁡ λ z = [ R N ( 1 − e 2 ) + h ] sin ⁡ L \begin{array}{l}x=\left(R_{N}+h\right) \cos L \cos \lambda \\ y=\left(R_{N}+h\right) \cos L \sin \lambda \\ z=\left[R_{N}\left(1-e^{2}\right)+h\right] \sin L\end{array} x=(RN​+h)cosLcosλy=(RN​+h)cosLsinλz=[RN​(1−e2)+h]sinL​

/* 大地坐标(纬度、经度和高程)转地心地固坐标 */
static Vector3d blh2ecef(const Vector3d &blh) {double coslat, sinlat, coslon, sinlon;double rnh, rn;coslat = cos(blh[0]);sinlat = sin(blh[0]);coslon = cos(blh[1]);sinlon = sin(blh[1]);rn  = RN(blh[0]);rnh = rn + blh[2];return {rnh * coslat * coslon, rnh * coslat * sinlon, (rnh - rn * WGS84_E1) * sinlat};
}

7、ecef2blh()：地心地固坐标转大地坐标

B 0 = arctan ⁡ ( Z ( 1 − e 2 ) p ) N k = a 1 − e 2 sin ⁡ 2 B k − 1 H k = p cos ⁡ B k − 1 − N k B k = arctan ⁡ ( z ( 1 − e 2 N k N k ) p ) \begin{array}{c}B_{0}=\arctan \left(\frac{Z}{\left(1-e^{2}\right) p}\right) \\ N_{k}=\frac{a}{\sqrt{1-e^{2} \sin ^{2} B_{k-1}}} \\ H_{k}=\frac{p}{\cos B_{k-1}}-N_{k} \\ B_{k}=\arctan \left(\frac{z}{\left(1-\frac{e^{2} N_{k}}{N_{k}}\right)\ p }\right)\end{array} B0​=arctan((1−e2)pZ​)Nk​=1−e2sin2Bk−1​ ​a​Hk​=cosBk−1​p​−Nk​Bk​=arctan ​(1−Nk​e2Nk​​) pz​ ​​

static Vector3d ecef2blh(const Vector3d &ecef) {double p = sqrt(ecef[0] * ecef[0] + ecef[1] * ecef[1]);double rn;double lat, lon;double h = 0, h2;// 初始状态lat = atan(ecef[2] / (p * (1.0 - WGS84_E1)));lon = 2.0 * atan2(ecef[1], ecef[0] + p);do {h2  = h;rn  = RN(lat);h   = p / cos(lat) - rn;lat = atan(ecef[2] / (p * (1.0 - WGS84_E1 * rn / (rn + h))));} while (fabs(h - h2) > 1.0e-4);return {lat, lon, h};
}

8、DRi()：n系相对位置转大地坐标相对位置

[ δ φ δ L δ H ] = [ ( R M + H ) − 1 0 0 0 ( R N + H ) − 1 0 0 0 − 1 ] [ δ p N δ p E δ p B ] \left[\begin{array}{l}\delta \varphi \\ \delta L \\ \delta H\end{array}\right]=\left[\begin{array}{ccc}\left(R_{M}+H\right)^{-1} & 0 & 0 \\ 0 & \left(R_{N}+H\right)^{-1} & 0 \\ 0 & 0 & -1 \end{array}\right]\left[\begin{array}{l}\delta \boldsymbol{p}_{N} \\ \delta \boldsymbol{p}_{E} \\ \delta \boldsymbol{p}_{B}\end{array}\right] ​δφδLδH​ ​= ​(RM​+H)−100​0(RN​+H)−10​00−1​ ​ ​δpN​δpE​δpB​​ ​

/* n系相对位置转大地坐标相对位置 */
static Matrix3d DRi(const Vector3d &blh) {Matrix3d dri = Matrix3d::Zero();Eigen::Vector2d rmn = meridianPrimeVerticalRadius(blh[0]);dri(0, 0) = 1.0 / (rmn[0] + blh[2]);dri(1, 1) = 1.0 / ((rmn[1] + blh[2]) * cos(blh[0]));dri(2, 2) = -1;return dri;
}

9、DR()：大地坐标相对位置转n系相对位置

[ δ φ δ L δ H ] = [ ( R M + H ) − 1 0 0 0 ( R N + H ) − 1 0 0 0 − 1 ] [ δ p N δ p E δ p B ] \left[\begin{array}{l}\delta \varphi \\ \delta L \\ \delta H\end{array}\right]=\left[\begin{array}{ccc}\left(R_{M}+H\right)^{-1} & 0 & 0 \\ 0 & \left(R_{N}+H\right)^{-1} & 0 \\ 0 & 0 & -1 \end{array}\right]\left[\begin{array}{l}\delta \boldsymbol{p}_{N} \\ \delta \boldsymbol{p}_{E} \\ \delta \boldsymbol{p}_{B}\end{array}\right] ​δφδLδH​ ​= ​(RM​+H)−100​0(RN​+H)−10​00−1​ ​ ​δpN​δpE​δpB​​ ​

/* 大地坐标相对位置转n系相对位置 */
static Matrix3d DR(const Vector3d &blh) {Matrix3d dr = Matrix3d::Zero();Eigen::Vector2d rmn = meridianPrimeVerticalRadius(blh[0]);dr(0, 0) = rmn[0] + blh[2];dr(1, 1) = (rmn[1] + blh[2]) * cos(blh[0]);dr(2, 2) = -1;return dr;
}

10、local2global()：局部坐标(在origin处展开)转大地坐标

在 enwn() 中被调用，为了方便能直接传入北东地（n 系）坐标计算 n 系相对于 e 系转动角速度在 n 系的投影。

static Vector3d local2global(const Vector3d &origin, const Vector3d &local) {Vector3d ecef0 = blh2ecef(origin);Matrix3d cn0e  = cne(origin);Vector3d ecef1 = ecef0 + cn0e * local;Vector3d blh1  = ecef2blh(ecef1);return blh1;
}

11、global2local()：大地坐标转局部坐标(在origin处展开)

好像整个程序中都没用到这个函数。

static Vector3d global2local(const Vector3d &origin, const Vector3d &global) {Vector3d ecef0 = blh2ecef(origin);Matrix3d cn0e  = cne(origin);Vector3d ecef1 = blh2ecef(global);return cn0e.transpose() * (ecef1 - ecef0);
}

static Pose global2local(const Vector3d &origin, const Pose &global) {Pose local;Vector3d ecef0 = blh2ecef(origin);Matrix3d cn0e  = cne(origin);Vector3d ecef1 = blh2ecef(global.t);Matrix3d cn1e  = cne(global.t);local.t = cn0e.transpose() * (ecef1 - ecef0);local.R = cn0e.transpose() * cn1e * global.R;return local;
}

12、iewe()：地球自转角速度投影到e系

ω i e e = [ 0 0 ω e ] T \boldsymbol{\omega}_{i e}^{e}=\left[\begin{array}{lll}0 & 0 & \omega_{e}\end{array}\right]^{T} ωiee​=[0​0​ωe​​]T

static Vector3d iewe() {return {0, 0, WGS84_WIE};
}

13、iewn()：地球自转角速度投影到n系

ω i e n = [ ω e cos ⁡ φ 0 − ω e sin ⁡ φ ] T \boldsymbol{\omega}_{i e}^{n}=\left[\begin{array}{lll}\omega_{e} \cos \varphi & 0 & -\omega_{e} \sin \varphi\end{array}\right]^{T} ωien​=[ωe​cosφ​0​−ωe​sinφ​]T

static Vector3d iewn(double lat) {return {WGS84_WIE * cos(lat), 0, -WGS84_WIE * sin(lat)};
}

也可以直接传入北东地（n 系）坐标计算：

static Vector3d iewn(const Vector3d &origin, const Vector3d &local) {Vector3d global = local2global(origin, local);return iewn(global[0]);
}

14、enwn()：n系相对于e系转动角速度投影到n系

由载体运动线速度和地球曲率引起，与东向、北向速度有关，与天向速度无关
ω e n n = [ v E R N + h − v N R M + h − v E tan ⁡ φ R N + h ] T \boldsymbol{\omega}_{e n}^{n}=\left[\begin{array}{lll}\frac{v_{E}}{R_{N}+h} & \frac{-v_{N}}{R_{M}+h} & -\frac{v_{E} \tan \varphi}{R_{N}+h}\end{array}\right]^{T} ωenn​=[RN​+hvE​​​RM​+h−vN​​​−RN​+hvE​tanφ​​]T

static Vector3d enwn(const Eigen::Vector2d &rmn, const Vector3d &blh, const Vector3d &vel) {return {vel[1] / (rmn[1] + blh[2]), -vel[0] / (rmn[0] + blh[2]), -vel[1] * tan(blh[0]) / (rmn[1] + blh[2])};
}

同样也可以直接传入北东地（n 系）坐标计算：

static Vector3d enwn(const Vector3d &origin, const Vector3d &local, const Vector3d &vel) {Vector3d global     = local2global(origin, local);Eigen::Vector2d rmn = meridianPrimeVerticalRadius(global[0]);return enwn(rmn, global, vel);
}

七、捷联惯导更新：insPropagation()

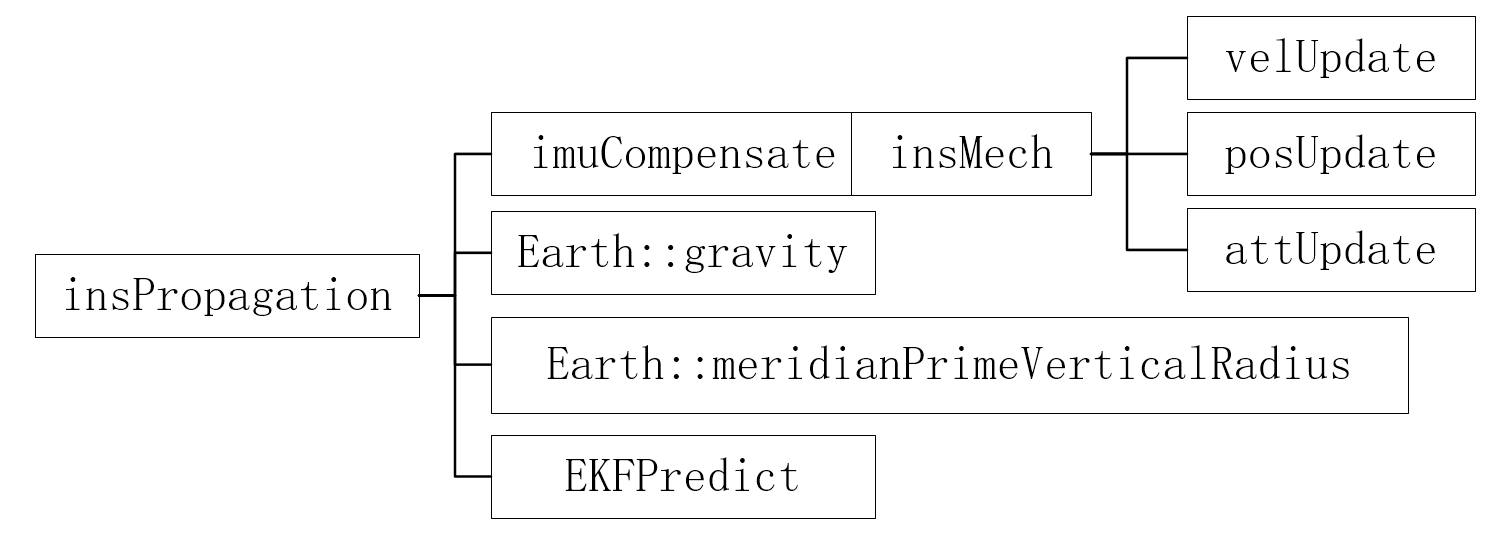
1、insPropagation()：捷联惯导递推

根据两帧的 IMU 量测，将系统状态和误差状态从前一个 IMU 时间递推到后一个 IMU 时间；主要有三个步骤：IMU 误差补偿、状态更新（机械编排）、噪声传播。

先调用 imuCompensate()，补偿当前时刻 IMU 量测，就是减去零偏、除以加上单位阵后的比例：

imuCompensate(imucur);

调用 insMech() 依次进行速度更新、位置更新、姿态更新：

INSMech::insMech(pvapre_, pvacur_, imupre, imucur);

之后一大段是噪声传播，后面详细介绍。

2、imuCompensate()：IMU数据误差补偿

减去零偏、除以加上单位阵后的比例：
diag ⁡ ( I + s ‾ g ) − 1 ( ω ~ i b b − b ‾ g ) = ω ^ i b b diag ⁡ ( I + s ‾ a ) − 1 ( f ~ i b b − b ‾ a ) = f ^ i b b \begin{array}{l}\operatorname{diag}\left(\boldsymbol{I}+\overline{\boldsymbol{s}}_{g}\right)^{-1}\left(\tilde{\boldsymbol{\omega}}_{i b}^{b}-\overline{\boldsymbol{b}}_{g}\right)=\hat{\boldsymbol{\omega}}_{i b}^{b} \\ \operatorname{diag}\left(\boldsymbol{I}+\overline{\boldsymbol{s}}_{a}\right)^{-1}\left(\tilde{\boldsymbol{f}}_{i b}^{b}-\overline{\boldsymbol{b}}_{a}\right)=\hat{\boldsymbol{f}}_{i b}^{b}\end{array} diag(I+sg​)−1(ω~ibb​−bg​)=ω^ibb​diag(I+sa​)−1(f~​ibb​−ba​)=f^​ibb​​

void GIEngine::imuCompensate(IMU &imu) {// 补偿IMU零偏// compensate the imu biasimu.dtheta -= imuerror_.gyrbias * imu.dt;imu.dvel -= imuerror_.accbias * imu.dt;// 补偿IMU比例因子// compensate the imu scaleEigen::Vector3d gyrscale, accscale;gyrscale   = Eigen::Vector3d::Ones() + imuerror_.gyrscale;accscale   = Eigen::Vector3d::Ones() + imuerror_.accscale;imu.dtheta = imu.dtheta.cwiseProduct(gyrscale.cwiseInverse());imu.dvel   = imu.dvel.cwiseProduct(accscale.cwiseInverse());
}

3、insMech()：IMU 状态更新（机械编排）

依次进行速度更新、位置更新、姿态更新，不可调换顺序。

void INSMech::insMech(const PVA &pvapre, PVA &pvacur, const IMU &imupre, const IMU &imucur) {// perform velocity update, position updata and attitude update in sequence, irreversible order// 依次进行速度更新、位置更新、姿态更新, 不可调换顺序velUpdate(pvapre, pvacur, imupre, imucur);posUpdate(pvapre, pvacur, imupre, imucur);attUpdate(pvapre, pvacur, imupre, imucur);
}

值得一提的是：

• PVA 更新都是先计算中间时刻，再由此计算当前时刻。
• 位置更新中：先计算 n 系到 e 系旋转四元数，再调用 blh()计算经纬度。
• 我觉得因为 PVA 写成三个函数，部分计算过程有重复，写在同一个函数实现能更简洁一些。

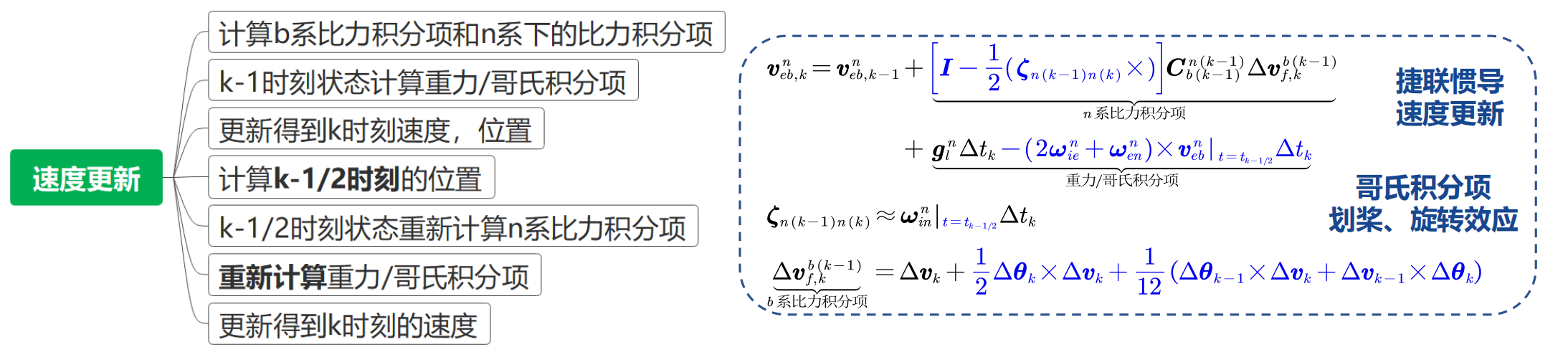
4、velUpdate()：速度更新

先定义解算过程中涉及的中间变量：

Eigen::Vector3d d_vfb, d_vfn, d_vgn, gl, midvel, midpos;
Eigen::Vector3d temp1, temp2, temp3;
Eigen::Matrix3d cnn, I33 = Eigen::Matrix3d::Identity();
Eigen::Quaterniond qne, qee, qnn, qbb, q1, q2;

调用 meridianPrimeVerticalRadius()，根据上一时刻位置计算子午圈、卯酉圈半径：
R M = R e ( 1 − e 2 ) ( 1 − e 2 sin ⁡ 2 L ) 3 / 2 、 R N = R e 1 − e 2 sin ⁡ 2 L R_{M}=\frac{R_{e}\left(1-e^{2}\right)}{\left(1-e^{2} \sin ^{2} L\right)^{3 / 2}}、R_{N}=\frac{R_{e}}{\sqrt{1-e^{2} \sin ^{2} L}} RM​=(1−e2sin2L)3/2Re​(1−e2)​、RN​=1−e2sin2L ​Re​​

Eigen::Vector2d rmrn = Earth::meridianPrimeVerticalRadius(pvapre.pos(0));

计算地球自转引起的导航系旋转 wie_n：
ω i e n = [ ω e cos ⁡ φ 0 − ω e sin ⁡ φ ] T \boldsymbol{\omega}_{i e}^{n}=\left[\begin{array}{lll}\omega_{e} \cos \varphi & 0 & -\omega_{e} \sin \varphi\end{array}\right]^{\mathrm{T}} ωien​=[ωe​cosφ​0​−ωe​sinφ​]T

wie_n << WGS84_WIE * cos(pvapre.pos[0]), 0, -WGS84_WIE * sin(pvapre.pos[0]);

计算载体在地球表面移动因地球曲率引起的导航系旋转 wen_n：
ω e n n = [ v E / ( R N + h ) − v N / ( R M + h ) − v E tan ⁡ φ / ( R N + h ) ] \boldsymbol{\omega}_{e n}^{n}=\left[\begin{array}{c}v_{E} /\left(R_{N}+h\right) \\ -v_{N} /\left(R_{M}+h\right) \\ -v_{E} \tan \varphi /\left(R_{N}+h\right)\end{array}\right] ωenn​= ​vE​/(RN​+h)−vN​/(RM​+h)−vE​tanφ/(RN​+h)​ ​

wen_n << pvapre.vel[1] / (rmrn[1] + pvapre.pos[2]), -pvapre.vel[0] / (rmrn[0] + pvapre.pos[2]),-pvapre.vel[1] * tan(pvapre.pos[0]) / (rmrn[1] + pvapre.pos[2]);

调用 gravity()，根据上一时刻位置计算 重力 gravity：
g L = 9.7803267715 × ( 1 + 0.0052790414 × sin ⁡ 2 L − 0.0000232718 × sin ⁡ 2 2 L ) + h × ( 0.0000000043977311 × sin ⁡ 2 L − 0.0000030876910891 ) + 0.0000000000007211 × sin ⁡ 4 2 L g_{L}=9.7803267715 \times\left(1+0.0052790414 \times \sin ^{2} L-0.0000232718 \times \sin ^{2} 2 L\right) \\ +h\times(0.0000000043977311\times\sin ^{2} L-0.0000030876910891)+0.0000000000007211\times\sin ^{4} 2 L gL​=9.7803267715×(1+0.0052790414×sin2L−0.0000232718×sin22L)+h×(0.0000000043977311×sin2L−0.0000030876910891)+0.0000000000007211×sin42L

double gravity = Earth::gravity(pvapre.pos);

计算 b 系比力积分项 d_vfb，单子样 + 前一周期补偿划桨效应：
Δ v f , k − 1 ) b ( k − 1 ) ⏟ b 系比力积分项  = Δ v k + 1 2 Δ θ k × Δ v k + 1 12 ( Δ θ k − 1 × Δ v k + Δ v k − 1 × Δ θ k ) \underbrace{\Delta \boldsymbol{v}_{f, k-1)}^{b(k-1)}}_{b \text { 系比力积分项 }}=\Delta \boldsymbol{v}_{k}+\frac{1}{2} \Delta \boldsymbol{\theta}_{k} \times \Delta \boldsymbol{v}_{k}+\frac{1}{12}\left(\Delta \boldsymbol{\theta}_{k-1} \times \Delta \boldsymbol{v}_{k}+\Delta \boldsymbol{v}_{k-1} \times \Delta \boldsymbol{\theta}_{k}\right) b 系比力积分项  Δvf,k−1)b(k−1)​​​=Δvk​+21​Δθk​×Δvk​+121​(Δθk−1​×Δvk​+Δvk−1​×Δθk​)

// 旋转效应和双子样划桨效应
// rotational and sculling motion
temp1 = imucur.dtheta.cross(imucur.dvel) / 2;
temp2 = imupre.dtheta.cross(imucur.dvel) / 12;
temp3 = imupre.dvel.cross(imucur.dtheta) / 12;
// b系比力积分项
// velocity increment due to the specific force
d_vfb = imucur.dvel + temp1 + temp2 + temp3;

比力积分项投影到 n 系，三行代码分别对应的公式为：
ω i n n = ω i e n + ω e n n {\omega}_{i n}^{n}={\omega}_{i e}^{n}+{\omega}_{e n}^{n} ωinn​=ωien​+ωenn​

ζ n ( k − 1 ) n ( k ) ≈ ω i n n ∣ t = t k − 1 / 2 Δ t k \left.\boldsymbol{\zeta}_{n(k-1) n(k)} \approx \boldsymbol{\omega}_{i n}^{n}\right|_{t=t_{k-1 / 2}} \Delta t_{k} ζn(k−1)n(k)​≈ωinn​ ​t=tk−1/2​​Δtk​

[ I − 1 2 ( ζ n ( k − 1 ) n ( k ) × ) ] C b ( k − 1 ) n ( k − 1 ) Δ v f , k b ( k − 1 ) ⏟ n 系比力积分项  \underbrace{\left[\boldsymbol{I}-\frac{1}{2}\left(\boldsymbol{\zeta}_{n(k-1) n(k)} \times\right)\right] \boldsymbol{C}_{b(k-1)}^{n(k-1)} \Delta \boldsymbol{v}_{f, k}^{b(k-1)}}_{n \text { 系比力积分项 }} n 系比力积分项  [I−21​(ζn(k−1)n(k)​×)]Cb(k−1)n(k−1)​Δvf,kb(k−1)​​​

// 比力积分项投影到n系
// velocity increment dut to the specfic force projected to the n-frame
temp1 = (wie_n + wen_n) * imucur.dt / 2;
cnn   = I33 - Rotation::skewSymmetric(temp1);
d_vfn = cnn * pvapre.att.cbn * d_vfb;

计算重力/哥式积分项：
g l n Δ t k − ( 2 ω i n + ω e n n ) × v e b n ∣ t = t k − 1 / 2 Δ t k ⏟ 重力/哥氏积分项  \underbrace{\boldsymbol{g}_{l}^{n} \Delta t_{k}-\left(2 \boldsymbol{\omega}_{i}^{n}+\boldsymbol{\omega}_{e n}^{n}\right) \times\left.\boldsymbol{v}_{e b}^{n}\right|_{t=t_{k-1 / 2}} \Delta t_{k}}_{\text {重力/哥氏积分项 }} 重力/哥氏积分项  gln​Δtk​−(2ωin​+ωenn​)×vebn​∣t=tk−1/2​​Δtk​​​

// 计算重力/哥式积分项
// velocity increment due to the gravity and Coriolis force
gl << 0, 0, gravity;
d_vgn = (gl - (2 * wie_n + wen_n).cross(pvapre.vel)) * imucur.dt;

上一时刻速度加上一半比力积分项和比力积分项，得到中间时刻速度：

// 得到中间时刻速度
// velocity at k-1/2
midvel = pvapre.vel + (d_vfn + d_vgn) / 2;

外推得到中间时刻位置：

• 计算两时刻n系旋转四元数 qnn
• 根据地球自转角速率，计算两时刻e系旋转四元数 qee
• 调用 qne 根据先前时刻位置，计算先前时刻n系到e系旋转四元数 qne
• 当前时刻 n 系到 e 系旋转四元数 qne = 两时刻e系旋转四元数 * 先前n系到e系旋转四元数 * 两时刻 n 系旋转四元数
• 中间时刻高程 = 先前高程 - 高程方向速度 * 一半采样周期（因为北东地，计算出的速度时地向的，所以减）
• 调用 blh() 根据 n系到e系旋转四元数计算经纬度

// 外推得到中间时刻位置
// position extrapolation to k-1/2
qnn = Rotation::rotvec2quaternion(temp1);
temp2 << 0, 0, -WGS84_WIE * imucur.dt / 2;
qee = Rotation::rotvec2quaternion(temp2);
qne = Earth::qne(pvapre.pos);
qne = qee * qne * qnn;
midpos[2] = pvapre.pos[2] - midvel[2] * imucur.dt / 2;
midpos    = Earth::blh(qne, midpos[2]);

基于用中间时刻的位置，重新做一遍之前的操作：

• 重新计算中间时刻的地理参数：rmrn、wie_n、wen_n（重力没重算）
• 重新计算 n 系下平均比力积分项：d_vfn
• 重新计算重力、哥式积分项：d_vgn

// 重新计算中间时刻的 rmrn, wie_e, wen_n
// recompute rmrn, wie_n, and wen_n at k-1/2
rmrn = Earth::meridianPrimeVerticalRadius(midpos[0]);
wie_n << WGS84_WIE * cos(midpos[0]), 0, -WGS84_WIE * sin(midpos[0]);
wen_n << midvel[1] / (rmrn[1] + midpos[2]), -midvel[0] / (rmrn[0] + midpos[2]),-midvel[1] * tan(midpos[0]) / (rmrn[1] + midpos[2]);// 重新计算n系下平均比力积分项
// recompute d_vfn
temp3 = (wie_n + wen_n) * imucur.dt / 2;
cnn   = I33 - Rotation::skewSymmetric(temp3);
d_vfn = cnn * pvapre.att.cbn * d_vfb;// 重新计算重力、哥式积分项
// recompute d_vgn
gl << 0, 0, Earth::gravity(midpos);
d_vgn = (gl - (2 * wie_n + wen_n).cross(midvel)) * imucur.dt;

最后，用上一时刻的速度，加上n系下平均比力积分项、重力/哥式积分项，得到当前时刻速度：
v e b , k n = v e b , k − 1 n + [ I − 1 2 ( ζ n ( k − 1 ) n ( k ) × ) ] C b ( k − 1 ) n ( k − 1 ) Δ v f , k b ( k − 1 ) ⏟ n 系比力积分项  + g l n Δ t k − ( 2 ω i n + ω e n n ) × v e b n ∣ t = t k − 1 / 2 Δ t k ⏟ 重力/哥氏积分项  \begin{aligned} \boldsymbol{v}_{e b, k}^{n}=\boldsymbol{v}_{e b, k-1}^{n} & +\underbrace{\left[\boldsymbol{I}-\frac{1}{2}\left(\boldsymbol{\zeta}_{n(k-1) n(k)} \times\right)\right] \boldsymbol{C}_{b(k-1)}^{n(k-1)} \Delta \boldsymbol{v}_{f, k}^{b(k-1)}}_{n \text { 系比力积分项 }} \\ & +\underbrace{\boldsymbol{g}_{l}^{n} \Delta t_{k}-\left(2 \boldsymbol{\omega}_{i}^{n}+\boldsymbol{\omega}_{e n}^{n}\right) \times\left.\boldsymbol{v}_{e b}^{n}\right|_{t=t_{k-1 / 2}} \Delta t_{k}}_{\text {重力/哥氏积分项 }}\end{aligned} veb,kn​=veb,k−1n​​+n 系比力积分项  [I−21​(ζn(k−1)n(k)​×)]Cb(k−1)n(k−1)​Δvf,kb(k−1)​​​+重力/哥氏积分项  gln​Δtk​−(2ωin​+ωenn​)×vebn​∣t=tk−1/2​​Δtk​​​​

pvacur.vel = pvapre.vel + d_vfn + d_vgn;

5、posUpdate()：位置更新

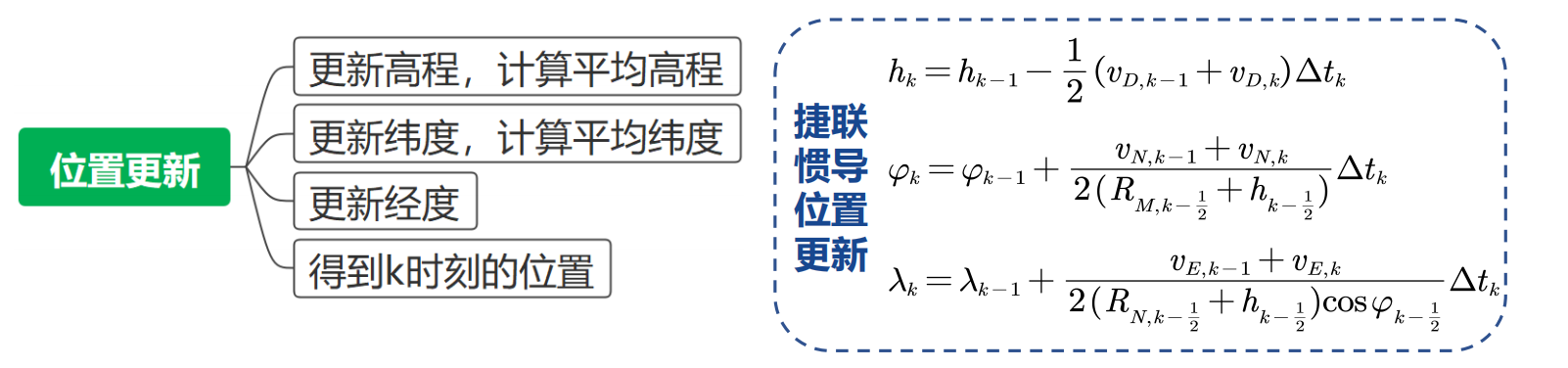
先定义解算过程中涉及的中间变量：

Eigen::Vector3d temp1, temp2, midvel, midpos;
Eigen::Quaterniond qne, qee, qnn;

重新计算中间时刻的速度 midvel 和位置 midpos：

• 中间时刻速度：取两时刻的平均。
• 中间时刻位置：上一时刻位置 + 平均速度 * 一半采样间隔。

// 重新计算中间时刻的速度和位置
// recompute velocity and position at k-1/2
midvel = (pvacur.vel + pvapre.vel) / 2;
midpos = pvapre.pos + Earth::DRi(pvapre.pos) * midvel * imucur.dt / 2;

根据中间时刻位置， 重新计算中间时刻地理参数（除了重力）：

// 重新计算中间时刻地理参数
// recompute rmrn, wie_n, wen_n at k-1/2
Eigen::Vector2d rmrn;
Eigen::Vector3d wie_n, wen_n;
rmrn = Earth::meridianPrimeVerticalRadius(midpos[0]);
wie_n << WGS84_WIE * cos(midpos[0]), 0, -WGS84_WIE * sin(midpos[0]);
wen_n << midvel[1] / (rmrn[1] + midpos[2]), -midvel[0] / (rmrn[0] + midpos[2]),-midvel[1] * tan(midpos[0]) / (rmrn[1] + midpos[2]);

重新计算 k 时刻到 k-1 时刻 n 系旋转矢量：
ω i n n = ω i e n + ω e n n {\omega}_{i n}^{n}={\omega}_{i e}^{n}+{\omega}_{e n}^{n} ωinn​=ωien​+ωenn​

ζ n ( k − 1 ) n ( k ) ≈ ω i n n ∣ t = t k − 1 / 2 Δ t k \left.\boldsymbol{\zeta}_{n(k-1) n(k)} \approx \boldsymbol{\omega}_{i n}^{n}\right|_{t=t_{k-1 / 2}} \Delta t_{k} ζn(k−1)n(k)​≈ωinn​ ​t=tk−1/2​​Δtk​

// 重新计算 k时刻到k-1时刻 n系旋转矢量
// recompute n-frame rotation vector (n(k) with respect to n(k-1)-frame)
temp1 = (wie_n + wen_n) * imucur.dt;
qnn   = Rotation::rotvec2quaternion(temp1);

e 系转动等效旋转矢量 (k-1时刻k时刻，所以取负号)，直接就是地球自转角速率乘以时间差：

// e系转动等效旋转矢量 (k-1时刻k时刻，所以取负号)
// e-frame rotation vector (e(k-1) with respect to e(k)-frame)
temp2 << 0, 0, -WGS84_WIE * imucur.dt;
qee = Rotation::rotvec2quaternion(temp2);

由先前时刻位置，调用 qne()，得到先前n系到e系旋转四元数：

qne = Earth::qne(pvapre.pos);

当前时刻n系到e系旋转四元数 = 两时刻e系旋转四元数 * 先前n系到e系旋转四元数 * 两时刻n系旋转四元数：

qne = qee * qne * qnn;

当前时刻高程 = 先前高程 - 高程方向速度 * 采样间隔（因为北东地，计算出的速度时地向的，所以减）：

pvacur.pos[2] = pvapre.pos[2] - midvel[2] * imucur.dt;

调用 blh() 根据 n 系到 e 系旋转四元数计算经纬度：

pvacur.pos = Earth::blh(qne, pvacur.pos[2]);

6、attUpdate()：姿态更新

先定义解算过程中涉及的中间变量：

Eigen::Quaterniond qne_pre, qne_cur, qne_mid, qnn, qbb;
Eigen::Vector3d temp1, midpos, midvel;

重新计算中间时刻的速度和位置，中间速度是两时刻平均、中间位置相对于是作了一次位置更新：

• 根据两时刻速度，计算平均速度 midvel
• 根据上一时刻位置计算n系到e系转换四元数 qne_pre
• 根据当前时刻位置计算n系到e系转换四元数 qne_cur
• 根据两时刻转换四元数，计算n系到e系平均转换四元数 qne_mid（注意得通过等效旋转矢量，并非直接插值）
• 计算当前中间时刻位置 midpos

// 重新计算中间时刻的速度和位置
// recompute velocity and position at k-1/2
midvel = (pvapre.vel + pvacur.vel) / 2;
qne_pre   = Earth::qne(pvapre.pos);
qne_cur   = Earth::qne(pvacur.pos);
temp1     = Rotation::quaternion2vector(qne_cur.inverse() * qne_pre);
qne_mid   = qne_pre * Rotation::rotvec2quaternion(temp1 / 2).inverse();
midpos[2] = (pvacur.pos[2] + pvapre.pos[2]) / 2;
midpos    = Earth::blh(qne_mid, midpos[2]);

重新计算中间时刻地理参数：

// 重新计算中间时刻地理参数
// recompute rmrn, wie_n, wen_n at k-1/2
Eigen::Vector2d rmrn;
Eigen::Vector3d wie_n, wen_n;
rmrn = Earth::meridianPrimeVerticalRadius(midpos[0]);
wie_n << WGS84_WIE * cos(midpos[0]), 0, -WGS84_WIE * sin(midpos[0]);
wen_n << midvel[1] / (rmrn[1] + midpos[2]), -midvel[0] / (rmrn[0] + midpos[2]),-midvel[1] * tan(midpos[0]) / (rmrn[1] + midpos[2]);

计算 n 系的旋转四元数 k-1 时刻到 k 时刻系旋转：
ω i n n = ω i e n + ω e n n {\omega}_{i n}^{n}={\omega}_{i e}^{n}+{\omega}_{e n}^{n} ωinn​=ωien​+ωenn​

ζ n ( k − 1 ) n ( k ) ≈ ω i n n ∣ t = t k − 1 / 2 Δ t k \left.\boldsymbol{\zeta}_{n(k-1) n(k)} \approx \boldsymbol{\omega}_{i n}^{n}\right|_{t=t_{k-1 / 2}} \Delta t_{k} ζn(k−1)n(k)​≈ωinn​ ​t=tk−1/2​​Δtk​

// 重新计算 k时刻到k-1时刻 n系旋转矢量
// recompute n-frame rotation vector (n(k) with respect to n(k-1)-frame)
temp1 = (wie_n + wen_n) * imucur.dt;
qnn   = Rotation::rotvec2quaternion(temp1);

计算 b 系旋转四元数补偿二阶圆锥误差：
q b k b k − 1 ← ϕ k = Δ θ k + 1 12 Δ θ k − 1 × Δ θ k \boldsymbol{q}_{b_{k}}^{b_{k-1}} \leftarrow \boldsymbol{\phi}_{k}=\Delta \boldsymbol{\theta}_{k}+\frac{1}{12} \Delta \boldsymbol{\theta}_{k-1} \times \Delta \boldsymbol{\theta}_{k} qbk​bk−1​​←ϕk​=Δθk​+121​Δθk−1​×Δθk​

// 计算b系旋转四元数 补偿二阶圆锥误差
// b-frame rotation vector (b(k) with respect to b(k-1)-frame)
// compensate the second-order coning correction term.
temp1 = imucur.dtheta + imupre.dtheta.cross(imucur.dtheta) / 12;
qbb   = Rotation::rotvec2quaternion(temp1);

两时刻n系的旋转四元数 * 上一时刻姿态四元数 * 两时刻b系旋转四元数得到当前姿态：
q b k n k = q n k − 1 n k q b k − 1 n k − 1 q b k b k − 1 \boldsymbol{q}_{b_{k}}^{n_{k}}=\boldsymbol{q}_{n_{k-1}}^{n_{k}} \boldsymbol{q}_{b_{k-1}}^{n_{k-1}} \boldsymbol{q}_{b_{k}}^{b_{k-1}} qbk​nk​​=qnk−1​nk​​qbk−1​nk−1​​qbk​bk−1​​

// 姿态更新完成
// attitude update finish
pvacur.att.qbn   = qnn * pvapre.att.qbn * qbb;
pvacur.att.cbn   = Rotation::quaternion2matrix(pvacur.att.qbn);
pvacur.att.euler = Rotation::matrix2euler(pvacur.att.cbn);

7、噪声传播

在 insPropagation() 函数中，IMU状态更新之后进行。

先要构建 F 矩阵：
F = [ F r r I 3 × 3 0 0 0 0 0 F v r F v v [ ( C b n f b ) × ] 0 C b n 0 C b n diag ⁡ ( f b ) F ϕ r F ϕ v − ( ω i n n × ) − C b n 0 − C b n diag ⁡ ( ω i b b ) 0 0 0 0 − 1 T g b I 3 × 3 0 0 0 0 0 0 0 − 1 T a b I 3 × 3 0 0 0 0 0 0 0 − 1 T g s I 3 × 3 0 0 0 0 0 0 0 − 1 T a s I 3 × 3 ] \mathbf{F}=\left[\begin{array}{ccccccc}\mathbf{F}_{r r} & \mathbf{I}_{3 \times 3} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{F}_{v r} & \mathbf{F}_{v v} & {\left[\left(\mathbf{C}_{b}^{n} \boldsymbol{f}^{b}\right) \times\right]} & \mathbf{0} & \mathbf{C}_{b}^{n} & \mathbf{0} & \mathbf{C}_{b}^{n} \operatorname{diag}\left(\boldsymbol{f}^{b}\right) \\ \mathbf{F}_{\phi r} & \mathbf{F}_{\phi v} & -\left(\boldsymbol{\omega}_{i n}^{n} \times\right) & -\mathbf{C}_{b}^{n} & \mathbf{0} & -\mathbf{C}_{b}^{n} \operatorname{diag}\left(\boldsymbol{\omega}_{i b}^{b}\right) & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \frac{-1}{T_{g b}} \mathbf{I}_{3 \times 3} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \frac{-1}{T_{a b}} \mathbf{I}_{3 \times 3} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \frac{-1}{T_{g s}} \mathbf{I}_{3 \times 3} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \frac{-1}{T_{a s}} \mathbf{I}_{3 \times 3}\end{array}\right] F= ​Frr​Fvr​Fϕr​0000​I3×3​Fvv​Fϕv​0000​0[(Cbn​fb)×]−(ωinn​×)0000​00−Cbn​Tgb​−1​I3×3​000​0Cbn​00Tab​−1​I3×3​00​00−Cbn​diag(ωibb​)00Tgs​−1​I3×3​0​0Cbn​diag(fb)0000Tas​−1​I3×3​​ ​
上面 F 矩阵每一块都是一个 $3\times 3$ 矩阵，分别表示位置、速度、姿态、陀螺仪零偏、加速度计零偏、陀螺仪比例、加速度计比力，共21维。可以很明显的看出左上角几乎是满的，因为位置、速度、姿态之间误差耦合很深；右下的器件误差很稀释，因为我们认为器件与器件之间的量测是相互独立的，处理在对角线上有元素之外，只在与器件相关的位置有元素（陀螺仪和姿态相关、加速度计和速度相关）。

定义了枚举值来索引左上角元素的下标：

enum StateID { P_ID = 0, V_ID = 3, PHI_ID = 6, BG_ID = 9, BA_ID = 12, SG_ID = 15, SA_ID = 18 };

代码排的很整齐，遵循从左往右、从上往下的顺序计算：

// 位置误差
// position error
temp.setZero();
temp(0, 0)                = -pvapre_.vel[2] / rmh;
temp(0, 2)                = pvapre_.vel[0] / rmh;
temp(1, 0)                = pvapre_.vel[1] * tan(pvapre_.pos[0]) / rnh;
temp(1, 1)                = -(pvapre_.vel[2] + pvapre_.vel[0] * tan(pvapre_.pos[0])) / rnh;
temp(1, 2)                = pvapre_.vel[1] / rnh;
F.block(P_ID, P_ID, 3, 3) = temp;
F.block(P_ID, V_ID, 3, 3) = Eigen::Matrix3d::Identity();// 速度误差
// velocity error
temp.setZero();
temp(0, 0) = -2 * pvapre_.vel[1] * WGS84_WIE * cos(pvapre_.pos[0]) / rmh -pow(pvapre_.vel[1], 2) / rmh / rnh / pow(cos(pvapre_.pos[0]), 2);
temp(0, 2) = pvapre_.vel[0] * pvapre_.vel[2] / rmh / rmh - pow(pvapre_.vel[1], 2) * tan(pvapre_.pos[0]) / rnh / rnh;
temp(1, 0) = 2 * WGS84_WIE * (pvapre_.vel[0] * cos(pvapre_.pos[0]) - pvapre_.vel[2] * sin(pvapre_.pos[0])) / rmh +pvapre_.vel[0] * pvapre_.vel[1] / rmh / rnh / pow(cos(pvapre_.pos[0]), 2);
temp(1, 2) = (pvapre_.vel[1] * pvapre_.vel[2] + pvapre_.vel[0] * pvapre_.vel[1] * tan(pvapre_.pos[0])) / rnh / rnh;
temp(2, 0) = 2 * WGS84_WIE * pvapre_.vel[1] * sin(pvapre_.pos[0]) / rmh;
temp(2, 2) = -pow(pvapre_.vel[1], 2) / rnh / rnh - pow(pvapre_.vel[0], 2) / rmh / rmh +2 * gravity / (sqrt(rmrn[0] * rmrn[1]) + pvapre_.pos[2]);
F.block(V_ID, P_ID, 3, 3) = temp;
temp.setZero();
temp(0, 0)                  = pvapre_.vel[2] / rmh;
temp(0, 1)                  = -2 * (WGS84_WIE * sin(pvapre_.pos[0]) + pvapre_.vel[1] * tan(pvapre_.pos[0]) / rnh);
temp(0, 2)                  = pvapre_.vel[0] / rmh;
temp(1, 0)                  = 2 * WGS84_WIE * sin(pvapre_.pos[0]) + pvapre_.vel[1] * tan(pvapre_.pos[0]) / rnh;
temp(1, 1)                  = (pvapre_.vel[2] + pvapre_.vel[0] * tan(pvapre_.pos[0])) / rnh;
temp(1, 2)                  = 2 * WGS84_WIE * cos(pvapre_.pos[0]) + pvapre_.vel[1] / rnh;
temp(2, 0)                  = -2 * pvapre_.vel[0] / rmh;
temp(2, 1)                  = -2 * (WGS84_WIE * cos(pvapre_.pos(0)) + pvapre_.vel[1] / rnh);
F.block(V_ID, V_ID, 3, 3)   = temp;
F.block(V_ID, PHI_ID, 3, 3) = Rotation::skewSymmetric(pvapre_.att.cbn * accel);
F.block(V_ID, BA_ID, 3, 3)  = pvapre_.att.cbn;
F.block(V_ID, SA_ID, 3, 3)  = pvapre_.att.cbn * (accel.asDiagonal());// 姿态误差
// attitude error
temp.setZero();
temp(0, 0) = -WGS84_WIE * sin(pvapre_.pos[0]) / rmh;
temp(0, 2) = pvapre_.vel[1] / rnh / rnh;
temp(1, 2) = -pvapre_.vel[0] / rmh / rmh;
temp(2, 0) = -WGS84_WIE * cos(pvapre_.pos[0]) / rmh - pvapre_.vel[1] / rmh / rnh / pow(cos(pvapre_.pos[0]), 2);
temp(2, 2) = -pvapre_.vel[1] * tan(pvapre_.pos[0]) / rnh / rnh;
F.block(PHI_ID, P_ID, 3, 3) = temp;
temp.setZero();
temp(0, 1)                    = 1 / rnh;
temp(1, 0)                    = -1 / rmh;
temp(2, 1)                    = -tan(pvapre_.pos[0]) / rnh;
F.block(PHI_ID, V_ID, 3, 3)   = temp;
F.block(PHI_ID, PHI_ID, 3, 3) = -Rotation::skewSymmetric(wie_n + wen_n);
F.block(PHI_ID, BG_ID, 3, 3)  = -pvapre_.att.cbn;
F.block(PHI_ID, SG_ID, 3, 3)  = -pvapre_.att.cbn * (omega.asDiagonal());// IMU零偏误差和比例因子误差，建模成一阶高斯-马尔科夫过程
// imu bias error and scale error, modeled as the first-order Gauss-Markov process
F.block(BG_ID, BG_ID, 3, 3) = -1 / options_.imunoise.corr_time * Eigen::Matrix3d::Identity();
F.block(BA_ID, BA_ID, 3, 3) = -1 / options_.imunoise.corr_time * Eigen::Matrix3d::Identity();
F.block(SG_ID, SG_ID, 3, 3) = -1 / options_.imunoise.corr_time * Eigen::Matrix3d::Identity();
F.block(SA_ID, SA_ID, 3, 3) = -1 / options_.imunoise.corr_time * Eigen::Matrix3d::Identity();

其中：
F r r = [ − v D R M + h 0 v N R M + h v E tan ⁡ φ R N + h − v D + v N tan ⁡ φ R N + h v E R N + h 0 0 0 ] \mathbf{F}_{r r}=\left[\begin{array}{ccc}-\frac{v_{D}}{R_{M}+h} & 0 & \frac{v_{N}}{R_{M}+h} \\ \frac{v_{E} \tan \varphi}{R_{N}+h} & -\frac{v_{D}+v_{N} \tan \varphi}{R_{N}+h} & \frac{v_{E}}{R_{N}+h} \\ 0 & 0 & 0\end{array}\right] Frr​= ​−RM​+hvD​​RN​+hvE​tanφ​0​0−RN​+hvD​+vN​tanφ​0​RM​+hvN​​RN​+hvE​​0​ ​

temp.setZero();
temp(0, 0) = -pvapre_.vel[2] / rmh;
temp(0, 2) = pvapre_.vel[0] / rmh;
temp(1, 0) = pvapre_.vel[1] * tan(pvapre_.pos[0]) / rnh;
temp(1, 1) = -(pvapre_.vel[2] + pvapre_.vel[0] * tan(pvapre_.pos[0])) / rnh;
temp(1, 2) = pvapre_.vel[1] / rnh;
F.block(P_ID, P_ID, 3, 3) = temp;

F v r = [ − 2 v E ω e cos ⁡ φ R M + h − v E 2 sec ⁡ 2 φ ( R M + h ) ( R N + h ) 0 v N v D ( R M + h ) 2 − v E 2 tan ⁡ φ ( R N + h ) 2 2 ω e ( v N cos ⁡ φ − v D sin ⁡ φ ) R M + h + v N v E sec ⁡ 2 φ ( R M + h ) ( R N + h ) 0 v E v D + v N v E tan ⁡ φ ( R N + h ) 2 2 ω e v E sin ⁡ φ R M + h 0 − v E 2 ( R N + h ) 2 − v N 2 ( R M + h ) 2 + 2 g p R M R N + h ] \mathbf{F}_{v r}=\left[\begin{array}{ccc}\frac{-2 v_{E} \omega_{e} \cos \varphi}{R_{M}+h}-\frac{v_{E}^{2} \sec ^{2} \varphi}{\left(R_{M}+h\right)\left(R_{N}+h\right)} & 0 & \frac{v_{N} v_{D}}{\left(R_{M}+h\right)^{2}}-\frac{v_{E}^{2} \tan \varphi}{\left(R_{N}+h\right)^{2}} \\ \frac{2 \omega_{e}\left(v_{N} \cos \varphi-v_{D} \sin \varphi\right)}{R_{M}+h}+\frac{v_{N} v_{E} \sec ^{2} \varphi}{\left(R_{M}+h\right)\left(R_{N}+h\right)} & 0 & \frac{v_{E} v_{D}+v_{N} v_{E} \tan \varphi}{\left(R_{N}+h\right)^{2}} \\ \frac{2 \omega_{e} v_{E} \sin \varphi}{R_{M}+h} & 0 & -\frac{v_{E}^{2}}{\left(R_{N}+h\right)^{2}}-\frac{v_{N}^{2}}{\left(R_{M}+h\right)^{2}}+\frac{2 g_{p}}{\sqrt{R_{M} R_{N}+h}}\end{array}\right] Fvr​= ​RM​+h−2vE​ωe​cosφ​−(RM​+h)(RN​+h)vE2​sec2φ​RM​+h2ωe​(vN​cosφ−vD​sinφ)​+(RM​+h)(RN​+h)vN​vE​sec2φ​RM​+h2ωe​vE​sinφ​​000​(RM​+h)2vN​vD​​−(RN​+h)2vE2​tanφ​(RN​+h)2vE​vD​+vN​vE​tanφ​−(RN​+h)2vE2​​−(RM​+h)2vN2​​+RM​RN​+h ​2gp​​​ ​

temp.setZero();
temp(0, 0) = -2 * pvapre_.vel[1] * WGS84_WIE * cos(pvapre_.pos[0]) / rmh -pow(pvapre_.vel[1], 2) / rmh / rnh / pow(cos(pvapre_.pos[0]), 2);
temp(0, 2) = pvapre_.vel[0] * pvapre_.vel[2] / rmh / rmh - pow(pvapre_.vel[1], 2) * tan(pvapre_.pos[0]) / rnh / rnh;
temp(1, 0) = 2 * WGS84_WIE * (pvapre_.vel[0] * cos(pvapre_.pos[0]) - pvapre_.vel[2] * sin(pvapre_.pos[0])) / rmh +pvapre_.vel[0] * pvapre_.vel[1] / rmh / rnh / pow(cos(pvapre_.pos[0]), 2);
temp(1, 2) = (pvapre_.vel[1] * pvapre_.vel[2] + pvapre_.vel[0] * pvapre_.vel[1] * tan(pvapre_.pos[0])) / rnh / rnh;
temp(2, 0) = 2 * WGS84_WIE * pvapre_.vel[1] * sin(pvapre_.pos[0]) / rmh;
temp(2, 2) = -pow(pvapre_.vel[1], 2) / rnh / rnh - pow(pvapre_.vel[0], 2) / rmh / rmh +2 * gravity / (sqrt(rmrn[0] * rmrn[1]) + pvapre_.pos[2]);
F.block(V_ID, P_ID, 3, 3) = temp;

F v v = [ v D R M + h − 2 ( ω e sin ⁡ φ + v E tan ⁡ φ R N + h ) v N R M + h 2 ω e sin ⁡ φ + v E tan ⁡ φ R N + h v D + v N tan ⁡ φ R N + h 2 ω e cos ⁡ φ + v E R N + h − 2 v N R M + h − 2 ( ω e cos ⁡ φ + v E R N + h ) 0 ] \mathbf{F}_{v v}=\left[\begin{array}{ccc}\frac{v_{D}}{R_{M}+h} & -2\left(\omega_{e} \sin \varphi+\frac{v_{E} \tan \varphi}{R_{N}+h}\right) & \frac{v_{N}}{R_{M}+h} \\ 2 \omega_{e} \sin \varphi+\frac{v_{E} \tan \varphi}{R_{N}+h} & \frac{v_{D}+v_{N} \tan \varphi}{R_{N}+h} & 2 \omega_{e} \cos \varphi+\frac{v_{E}}{R_{N}+h} \\ -\frac{2 v_{N}}{R_{M}+h} & -2\left(\omega_{e} \cos \varphi+\frac{v_{E}}{R_{N}+h}\right) & 0\end{array}\right] Fvv​= ​RM​+hvD​​2ωe​sinφ+RN​+hvE​tanφ​−RM​+h2vN​​​−2(ωe​sinφ+RN​+hvE​tanφ​)RN​+hvD​+vN​tanφ​−2(ωe​cosφ+RN​+hvE​​)​RM​+hvN​​2ωe​cosφ+RN​+hvE​​0​ ​

temp.setZero();
temp(0, 0) = pvapre_.vel[2] / rmh;
temp(0, 1) = -2 * (WGS84_WIE * sin(pvapre_.pos[0]) + pvapre_.vel[1] * tan(pvapre_.pos[0]) / rnh);
temp(0, 2) = pvapre_.vel[0] / rmh;
temp(1, 0) = 2 * WGS84_WIE * sin(pvapre_.pos[0]) + pvapre_.vel[1] * tan(pvapre_.pos[0]) / rnh;
temp(1, 1) = (pvapre_.vel[2] + pvapre_.vel[0] * tan(pvapre_.pos[0])) / rnh;
temp(1, 2) = 2 * WGS84_WIE * cos(pvapre_.pos[0]) + pvapre_.vel[1] / rnh;
temp(2, 0) = -2 * pvapre_.vel[0] / rmh;
temp(2, 1) = -2 * (WGS84_WIE * cos(pvapre_.pos(0)) + pvapre_.vel[1] / rnh);
F.block(V_ID, V_ID, 3, 3)   = temp;

F ϕ r = [ − ω e sin ⁡ φ R M + h 0 v E ( R N + h ) 2 0 0 − v N ( R M + h ) 2 − ω e cos ⁡ φ R M + h − v E sec ⁡ 2 φ ( R M + h ) ( R N + h ) 0 − v E tan ⁡ φ ( R N + h ) 2 ] \mathbf{F}_{\phi r}=\left[\begin{array}{ccc}-\frac{\omega_{e} \sin \varphi}{R_{M}+h} & 0 & \frac{v_{E}}{\left(R_{N}+h\right)^{2}} \\ 0 & 0 & -\frac{v_{N}}{\left(R_{M}+h\right)^{2}} \\ -\frac{\omega_{e} \cos \varphi}{R_{M}+h}-\frac{v_{E} \sec ^{2} \varphi}{\left(R_{M}+h\right)\left(R_{N}+h\right)} & 0 & -\frac{v_{E} \tan \varphi}{\left(R_{N}+h\right)^{2}}\end{array}\right] Fϕr​= ​−RM​+hωe​sinφ​0−RM​+hωe​cosφ​−(RM​+h)(RN​+h)vE​sec2φ​​000​(RN​+h)2vE​​−(RM​+h)2vN​​−(RN​+h)2vE​tanφ​​ ​

temp.setZero();
temp(0, 0) = -WGS84_WIE * sin(pvapre_.pos[0]) / rmh;
temp(0, 2) = pvapre_.vel[1] / rnh / rnh;
temp(1, 2) = -pvapre_.vel[0] / rmh / rmh;
temp(2, 0) = -WGS84_WIE * cos(pvapre_.pos[0]) / rmh - pvapre_.vel[1] / rmh / rnh / pow(cos(pvapre_.pos[0]), 2);
temp(2, 2) = -pvapre_.vel[1] * tan(pvapre_.pos[0]) / rnh / rnh;
F.block(PHI_ID, P_ID, 3, 3) = temp;

F ϕ v = [ 0 1 R N + h 0 − 1 R M + h 0 0 0 − tan ⁡ φ R N + h 0 ] \mathbf{F}_{\phi v}=\left[\begin{array}{ccc}0 & \frac{1}{R_{N}+h} & 0 \\ -\frac{1}{R_{M}+h} & 0 & 0 \\ 0 & -\frac{\tan \varphi}{R_{N}+h} & 0\end{array}\right] Fϕv​= ​0−RM​+h1​0​RN​+h1​0−RN​+htanφ​​000​ ​

temp.setZero();
temp(0, 1) = 1 / rnh;
temp(1, 0) = -1 / rmh;
temp(2, 1) = -tan(pvapre_.pos[0]) / rnh;
F.block(PHI_ID, V_ID, 3, 3)   = temp;

IMU零偏误差和比例因子误差，建模成一阶高斯-马尔科夫过程，：
− 1 T g s I 3 × 3 \frac{-1}{T_{g s}} \mathbf{I}_{3 \times 3} Tgs​−1​I3×3​

// IMU零偏误差和比例因子误差，建模成一阶高斯-马尔科夫过程
// imu bias error and scale error, modeled as the first-order Gauss-Markov process
F.block(BG_ID, BG_ID, 3, 3) = -1 / options_.imunoise.corr_time * Eigen::Matrix3d::Identity();
F.block(BA_ID, BA_ID, 3, 3) = -1 / options_.imunoise.corr_time * Eigen::Matrix3d::Identity();
F.block(SG_ID, SG_ID, 3, 3) = -1 / options_.imunoise.corr_time * Eigen::Matrix3d::Identity();
F.block(SA_ID, SA_ID, 3, 3) = -1 / options_.imunoise.corr_time * Eigen::Matrix3d::Identity();

然后构建系统噪声驱动矩阵：
G 18 21 × 18 = [ 0 0 0 0 0 0 C b n 0 0 0 0 0 0 C b n 0 0 0 0 0 0 I 3 × 3 0 0 0 0 0 0 I 3 × 3 0 0 0 0 0 0 I 3 × 3 0 0 0 0 0 0 I 3 × 3 ] \underset{21 \times 18}{\mathbf{G}_{18}}=\left[\begin{array}{cccccc}\mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{C}_{b}^{n} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{C}_{b}^{n} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{I}_{3 \times 3} & \mathbf{0} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I}_{3 \times 3} & \mathbf{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I}_{3 \times 3} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{0} & \mathbf{I}_{3 \times 3}\end{array}\right] 21×18G18​​= ​0Cbn​00000​00Cbn​0000​000I3×3​000​0000I3×3​00​00000I3×3​0​000000I3×3​​ ​

// 系统噪声驱动矩阵
// system noise driven matrix
G.block(V_ID, VRW_ID, 3, 3)    = pvapre_.att.cbn;
G.block(PHI_ID, ARW_ID, 3, 3)  = pvapre_.att.cbn;
G.block(BG_ID, BGSTD_ID, 3, 3) = Eigen::Matrix3d::Identity();
G.block(BA_ID, BASTD_ID, 3, 3) = Eigen::Matrix3d::Identity();
G.block(SG_ID, SGSTD_ID, 3, 3) = Eigen::Matrix3d::Identity();
G.block(SA_ID, SASTD_ID, 3, 3) = Eigen::Matrix3d::Identity();

系统传播噪声的状态转移矩阵：
Φ k / k − 1 = I + F k − 1 Δ t k \boldsymbol{\Phi}_{k / k-1}=\boldsymbol{I}+\boldsymbol{F}_{k-1} \Delta t_{k} Φk/k−1​=I+Fk−1​Δtk​

// 状态转移矩阵
// compute the state transition matrix
Phi.setIdentity();
Phi = Phi + F * imucur.dt; 

系统传播噪声：
Q k = ( Φ k / k − 1 G k − 1 q k − 1 G k − 1 T Φ k / k − 1 T + G k q k G k T ) Δ t k / 2 \boldsymbol{Q}_{k}=\left(\begin{array}{c}\boldsymbol{\Phi}_{k / k-1} \boldsymbol{G}_{k-1} \boldsymbol{q}_{k-1} \boldsymbol{G}_{k-1}^{T} \boldsymbol{\Phi}_{k / k-1}^{T} \\ +\boldsymbol{G}_{k} \boldsymbol{q}_{k} \boldsymbol{G}_{k}^{T}\end{array}\right) \Delta t_{k} / 2 Qk​=(Φk/k−1​Gk−1​qk−1​Gk−1T​Φk/k−1T​+Gk​qk​GkT​​)Δtk​/2

// 计算系统传播噪声
// compute system propagation noise
Qd = G * Qc_ * G.transpose() * imucur.dt;
Qd = (Phi * Qd * Phi.transpose() + Qd) / 2;

EKF 预测传播系统协方差和系统误差状态：
x k / k − 1 = Φ k / k − 1 x k − 1 P k / k − 1 = Φ k / k − 1 P k − 1 Φ k / k − 1 T + Q k \begin{aligned} \boldsymbol{x}_{k / k-1} & =\boldsymbol{\Phi}_{k / k-1} \boldsymbol{x}_{k-1} \\ \boldsymbol{P}_{k / k-1} & =\boldsymbol{\Phi}_{k / k-1} \boldsymbol{P}_{k-1} \boldsymbol{\Phi}_{k / k-1}^{T}+\boldsymbol{Q}_{k}\end{aligned} xk/k−1​Pk/k−1​​=Φk/k−1​xk−1​=Φk/k−1​Pk−1​Φk/k−1T​+Qk​​

EKFPredict(Phi, Qd);

void GIEngine::EKFPredict(Eigen::MatrixXd &Phi, Eigen::MatrixXd &Qd) {assert(Phi.rows() == Cov_.rows());assert(Qd.rows() == Cov_.rows());// 传播系统协方差和误差状态// propagate system covariance and error stateCov_ = Phi * Cov_ * Phi.transpose() + Qd;dx_  = Phi * dx_;
}

八、GNSS 量测更新、系统状态反馈

1、gnssUpdate()：GNSS 量测更新

先将 IMU 位置 pvacur_.pos 转到 GNSS 天线相位中心位置 antenna_pos：
r ^ G = r ^ I + D R − 1 C ^ b n l b \hat{\boldsymbol{r}}_{G}=\hat{\boldsymbol{r}}_{I}+\boldsymbol{D}_{R}^{-1} \hat{\boldsymbol{C}}_{b}^{n} \boldsymbol{l}^{b} r^G​=r^I​+DR−1​C^bn​lb

// IMU位置转到GNSS天线相位中心位置
// convert IMU position to GNSS antenna phase center position
Eigen::Vector3d antenna_pos;
Eigen::Matrix3d Dr, Dr_inv;
Dr_inv      = Earth::DRi(pvacur_.pos);
Dr          = Earth::DR(pvacur_.pos);
antenna_pos = pvacur_.pos + Dr_inv * pvacur_.att.cbn * options_.antlever;

计算位置观测向量：IMU 预测天线位置减去 GNSS 观测位置：
z r = D R ( r ^ G − r ~ G ) \boldsymbol{z}_{r}=\boldsymbol{D}_{R}\left(\hat{\boldsymbol{r}}_{G}-\tilde{\boldsymbol{r}}_{G}\right) zr​=DR​(r^G​−r~G​)

// GNSS位置测量新息
// compute GNSS position innovation
Eigen::MatrixXd dz;
dz = Dr * (antenna_pos - gnssdata.blh);

构造 GNSS 位置观测矩阵：
H r = [ I 3 0 3 ( C b n l b ) × 0 3 0 3 0 3 0 3 ] \boldsymbol{H}_{r}=\left[\begin{array}{lllllll}\boldsymbol{I}_{3} & 0_{3} & \left(\boldsymbol{C}_{b}^{n} \boldsymbol{l}^{b}\right) \times & 0_{3} & 0_{3} & 0_{3} & 0_{3}\end{array}\right] Hr​=[I3​​03​​(Cbn​lb)×​03​​03​​03​​03​​]

// 构造GNSS位置观测矩阵
// construct GNSS position measurement matrix
Eigen::MatrixXd H_gnsspos;
H_gnsspos.resize(3, Cov_.rows());
H_gnsspos.setZero();
H_gnsspos.block(0, P_ID, 3, 3)   = Eigen::Matrix3d::Identity();
H_gnsspos.block(0, PHI_ID, 3, 3) = Rotation::skewSymmetric(pvacur_.att.cbn * options_.antlever);

位置观测噪声阵，就是用数据文件中读取到的 GNSS 位置标准差平方得到协方差，组成成协方差阵：

// 位置观测噪声阵
// construct measurement noise matrix
Eigen::MatrixXd R_gnsspos;
R_gnsspos = gnssdata.std.cwiseProduct(gnssdata.std).asDiagonal();

得到观测向量z，观测矩阵H, 观测噪声矩阵R后，调用 EKFUpdate()，量测更新：

EKFUpdate(dz, H_gnsspos, R_gnsspos);

最后，GNSS更新之后设置为不可用：

gnssdata.isvalid = false;

2、EKFUpdate()：EKF 更新协方差和误差状态

判断矩阵维度是否合理，不合理直接退出程序：

assert(H.cols() == Cov_.rows());
assert(dz.rows() == H.rows());
assert(dz.rows() == R.rows());
assert(dz.cols() == 1);

计算 Kalman 滤波增益系数 K：
K k = P k / k − 1 H k T ( H k P k / k − 1 H k T + R k ) − 1 \boldsymbol{K}_{k}=\boldsymbol{P}_{k / k-1} \boldsymbol{H}_{k}^{T}\left(\boldsymbol{H}_{k} \boldsymbol{P}_{k / k-1} \boldsymbol{H}_{k}^{T}+\boldsymbol{R}_{k}\right)^{-1} Kk​=Pk/k−1​HkT​(Hk​Pk/k−1​HkT​+Rk​)−1

// 计算Kalman增益
// Compute Kalman Gain
auto temp = H * Cov_ * H.transpose() + R;
Eigen::MatrixXd K = Cov_ * H.transpose() * temp.inverse();

更新系统误差状态和协方差：
P k = ( I − K k H k ) P k / k − 1 ( I − K k H k ) T + K k R k K k T K k = P k / k − 1 H k T ( H k P k / k − 1 H k T + R k ) − 1 \begin{array}{l}\boldsymbol{P}_{k}=\left(\boldsymbol{I}-\boldsymbol{K}_{k} \boldsymbol{H}_{k}\right) \boldsymbol{P}_{k / k-1}\left(\boldsymbol{I}-\boldsymbol{K}_{k} \boldsymbol{H}_{k}\right)^{T}+\boldsymbol{K}_{k} \boldsymbol{R}_{k} \boldsymbol{K}_{k}^{T} \\ \boldsymbol{K}_{k}=\boldsymbol{P}_{k / k-1} \boldsymbol{H}_{k}^{T}\left(\boldsymbol{H}_{k} \boldsymbol{P}_{k / k-1} \boldsymbol{H}_{k}^{T}+\boldsymbol{R}_{k}\right)^{-1}\end{array} Pk​=(I−Kk​Hk​)Pk/k−1​(I−Kk​Hk​)T+Kk​Rk​KkT​Kk​=Pk/k−1​HkT​(Hk​Pk/k−1​HkT​+Rk​)−1​

// 更新系统误差状态和协方差
// update system error state and covariance
Eigen::MatrixXd I;
I.resizeLike(Cov_);
I.setIdentity();
I = I - K * H;
// 如果每次更新后都进行状态反馈，则更新前dx_一直为0，下式可以简化为：dx_ = K * dz;
// if state feedback is performed after every update, dx_ is always zero before the update
// the following formula can be simplified as : dx_ = K * dz;
dx_  = dx_ + K * (dz - H * dx_);
Cov_ = I * Cov_ * I.transpose() + K * R * K.transpose();

3、stateFeedback()：状态反馈

想清楚卡尔曼滤波到底算的是什么，考虑到底是加还是减。零偏、比例因子残差是加、速度位置残差是减，反馈之后误差状态置 0：

void GIEngine::stateFeedback() {Eigen::Vector3d vectemp;// 位置误差反馈// posisiton error feedbackEigen::Vector3d delta_r = dx_.block(P_ID, 0, 3, 1);Eigen::Matrix3d Dr_inv  = Earth::DRi(pvacur_.pos);pvacur_.pos -= Dr_inv * delta_r;// 速度误差反馈// velocity error feedbackvectemp = dx_.block(V_ID, 0, 3, 1);pvacur_.vel -= vectemp;// 姿态误差反馈// attitude error feedbackvectemp                = dx_.block(PHI_ID, 0, 3, 1);Eigen::Quaterniond qpn = Rotation::rotvec2quaternion(vectemp);pvacur_.att.qbn        = qpn * pvacur_.att.qbn;pvacur_.att.cbn        = Rotation::quaternion2matrix(pvacur_.att.qbn);pvacur_.att.euler      = Rotation::matrix2euler(pvacur_.att.cbn);// IMU零偏误差反馈// IMU bias error feedbackvectemp = dx_.block(BG_ID, 0, 3, 1);imuerror_.gyrbias += vectemp;vectemp = dx_.block(BA_ID, 0, 3, 1);imuerror_.accbias += vectemp;// IMU比例因子误差反馈// IMU sacle error feedbackvectemp = dx_.block(SG_ID, 0, 3, 1);imuerror_.gyrscale += vectemp;vectemp = dx_.block(SA_ID, 0, 3, 1);imuerror_.accscale += vectemp;// 误差状态反馈到系统状态后,将误差状态清零// set 'dx' to zero after feedback error state to system statedx_.setZero();
}

九、KF-GINS常见问题

复制自PPT

KF-GINS能够达到怎么样的定位精度？

组合导航算法精度更受IMU等级、以及测试时GNSS定位质量影响。组合导航算法相对成熟，对于同样的设备只要算法正确实现，算法几乎不会对定位精度产生较大影响。

初始导航状态和初始导航状态标准差如何给定？

• 初始位置(和速度)可由GNSS给定，初始姿态(和速度)可从参考结果中获取；

• 位置速度标准差可由GNSS给定，姿态标准差可给经验值，车载领域一般横滚俯仰小，航向大一些

IMU数据输入到程序之前，需要扣除重力加速度吗？

不需要，惯性导航算法中补偿了重力加速度

INS机械编排中旋转效应等补偿项，对于低端IMU是否需要补偿？

低端IMU测量噪声更大，简化的IMU积分算法对低端IMU精度产生的影响较小

组合导航中GNSS信号丢失期间进行纯惯导解算，这时IMU误差项可以补偿吗？

GNSS丢失期间IMU误差项不更新，但是可以利用之前估计的IMU误差项继续补偿

IMU数据，如何从速率形式转到增量形式？

一般采用更高频率速率数据积分得到增量数据，参考：新手入门系列4——MEMS IMU原始数

据采集和时间同步的那些坑(i2Nav网站)

IMU零偏和比例因子建模时相关时间如何给定？

建模为一阶高斯-马尔可夫过程，实际中一般根据经验设置相关时间，MEMS设置1h

GNSS/INS组合导航中是否需要考虑惯性系和车体系的转换？

不需要，GNSS/INS组合导航不受载体限制，不需要考虑车体系

初始化拓展

• 动态初始对准，GNSS位置差分速度(或者GNSS直接输出速度)，位置差分计算初始航向

• 快速航向初始化 ，轨迹匹配方法快速获取准确初始航向

• 静态粗对准，适用于高精度惯导，双矢量法找到初始姿态

观测信息拓展

• 直接构建观测向量、观测模型和噪声矩阵，调用EKFUpdate更新和stateFeedback反馈

• GNSS速度观测信息、NHC约束信息(对于车载)、零速信息修正

状态信息拓展

• 如果需要增广系统状态(如里程计增广比例因子[2])，则修改RANK(NOISERANK)，添加StateID, NoiseID
• 协方差、状态转移矩阵、观测信息对应修改；添加观测信息，进行更新反馈

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！