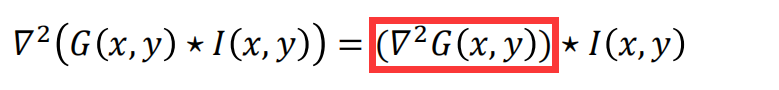国科大人工智能学院《计算机视觉》课 —底层视觉—深度学习与卷积神经网络、图像底层特征提取
提纲:
- 深度学习与卷积神经网络
- 图像底层特征提取:边缘、特征点
零、计算机视觉
- 计算机视觉的研究目标:使计算机具有 通过一幅或多幅图像 认知周围环境信息的能力
- 计算机视觉的研究主题:特征提取与匹配、图像分割、目标识别、三维重建、视觉跟踪、行为分析
一、深度学习的发展历史:人工神经网络、浅层学习、深度学习
要理清楚老师讲的这块的“来龙去脉”,是层层递进的。
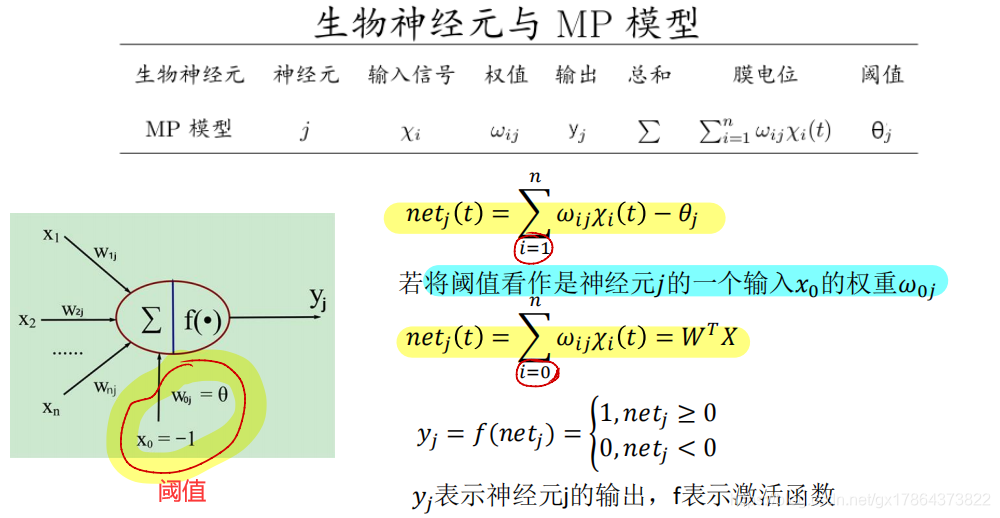
- 人工神经网络:多输入单输出、兴奋性神经元和抑制性神经元、阈值特性
- 生物神经元 —> MP模型
- 感知机的本质是MP模型。
- 浅层学习:单层感知机
- 感知机(单层线性神经网络)只对线性问题具有分类能力。
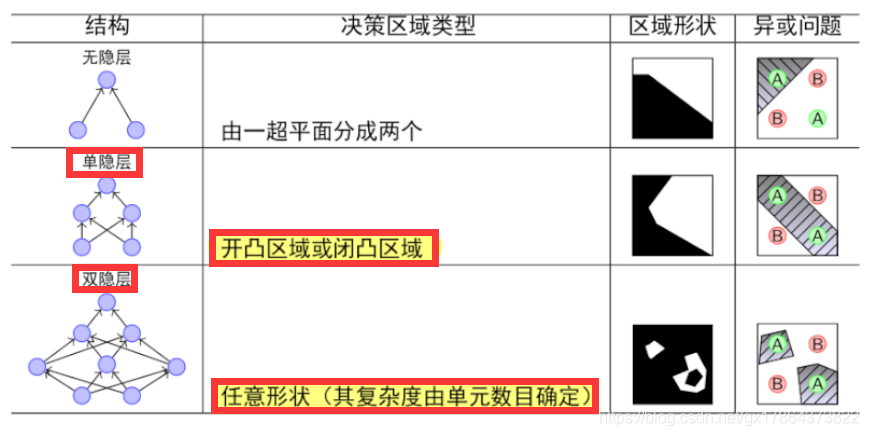
- 深度学习:多层感知机(单隐层感知机、双隐层感知机)
- 多层感知机:在输入层和输出层之间加入隐层,以形成能够将样本正确分类的凸域。
- 随着隐层层数的增多,凸域可以形成任意的形状,所以可以解决任何复杂的分类问题。
- “双隐层感知器就能解决任何复杂的分类问题”
- 但对于多层感知机来说,其隐层的权值很难训练(因为隐层节点不存在期望的输出,所以无法通过感知器的学习规则来训练多层感知器)。“心有余而力不足”(虽然武力高强,但却无力可施)~
- 所以产生了BP算法:误差逆传播。
- 以BP算法实现的多层感知器网络就是 BP网络。
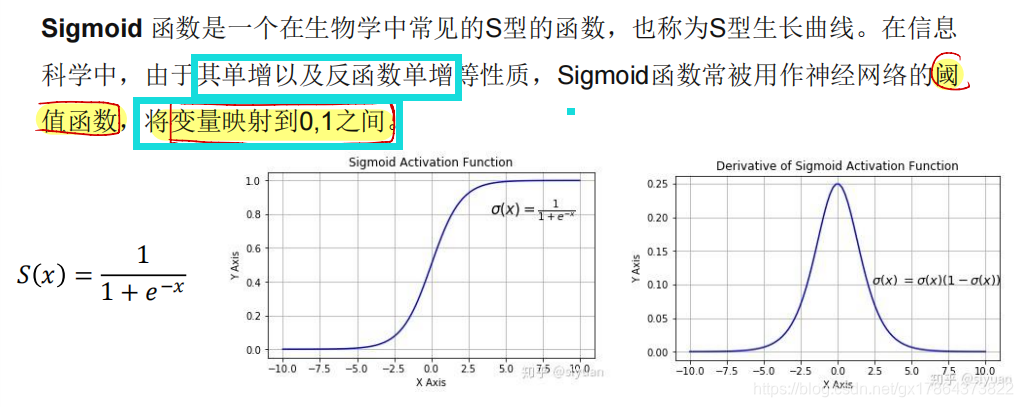
- 算法采用Sigmoid函数进行非线性映射,有效的解决了非线性分类和学习的问题。
- sigmoid函数缺点:梯度消失
梯度消失:Sigmoid函数趋近0和1的时候变化率会变得平坦,即Sigmoid的梯度趋近于0。神经网络使用Sigmoid激活函数进行反向传播时,输出接近0或1的神经元其梯度趋近于0。这些神经元叫饱和神经元。所以,饱和神经元的权值不会更新。并且,与此类神经元相连的神经元的权重也会更新的很慢。
- 梯度消失问题的解决方案:无监督预训练 对权值进行初始化 + 有监督训练 微调
- ReLU激活函数:增大了收敛速度,从根本上解决了梯度消失的问题。
- DNN:语音识别、图像识别(极大地降低了其识别错误率)
- AlexNet:构建的CNN网络
二、深度学习的常用模型
- CNN(Convolutional Neural Network)卷积神经网络
- 当图像像素作为神经网络输入数据时面临的问题:
- 权值共享:降低训练参数
- 局部感受野:卷积核的大小来控制局部感受野的大小
感受野:某个神经元能看到的输入图像的区域(全连接 -> 局部连接)
- 卷积
- 池化(下采样):降低平移敏感性、降维
-
理解卷积运算
-
全连接 —> 局部连接:感受野
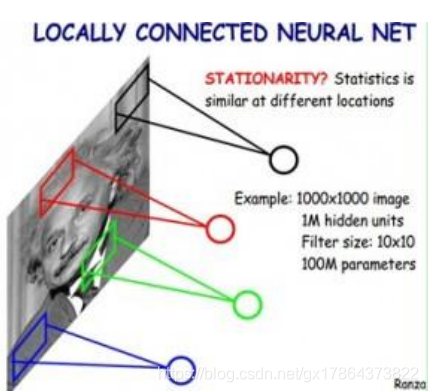
-
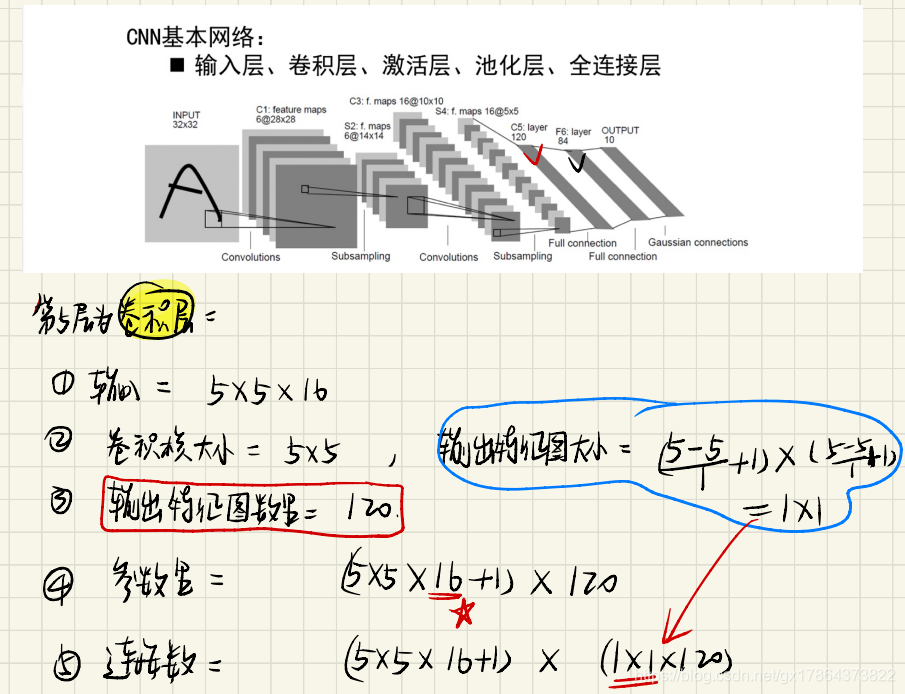
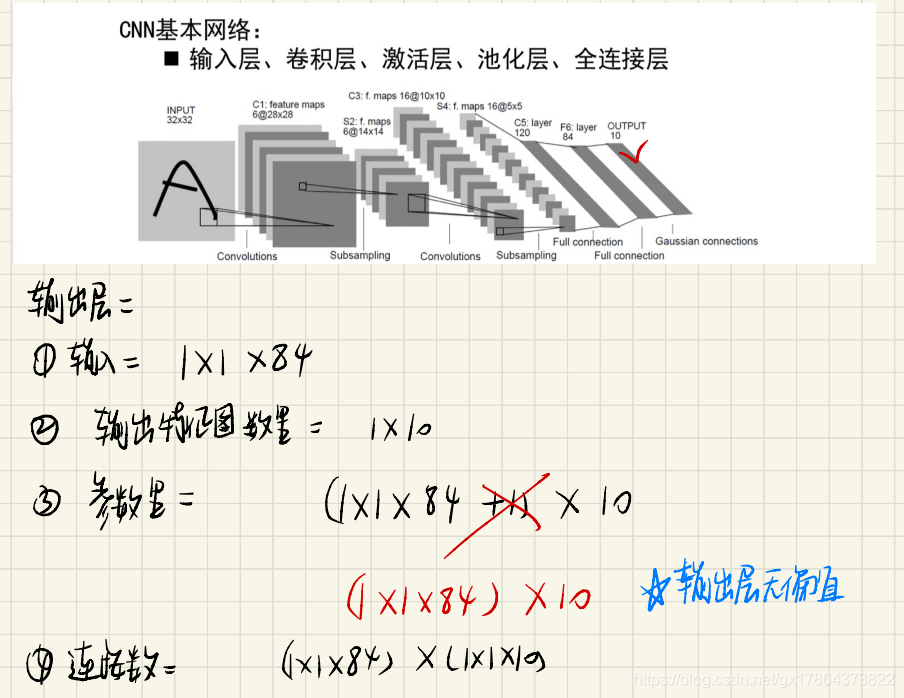
CNN基本结构:输入层、卷积层、激活层、池化层、全连接层
- CNN的优点:通过感受野和权值共享减少了神经网络需训练的参数个数。
- 以LeNet-5为例,要会计算每层的 特征图大小、参数个数和连接数。
-
CNN中常用的激活函数
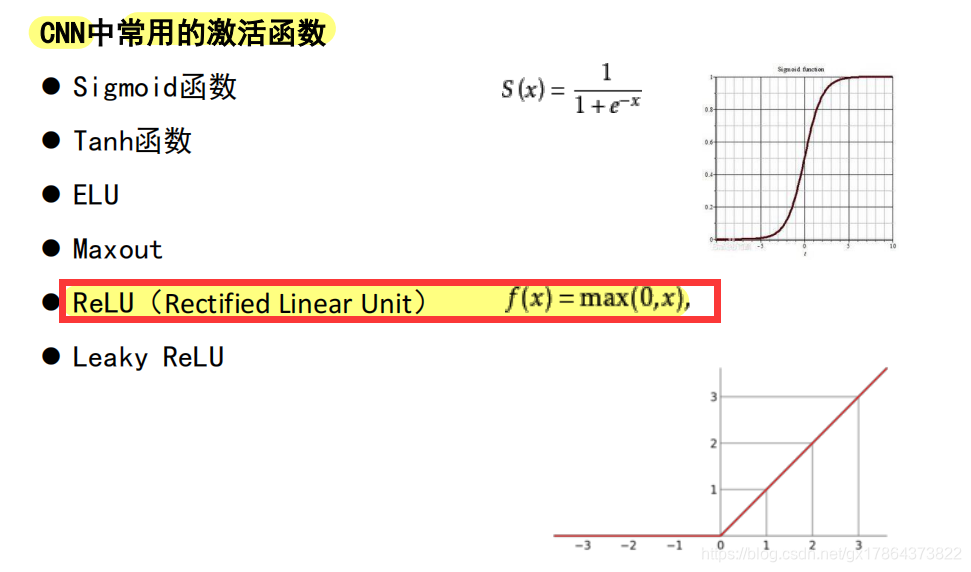
-
开发平台:Caffe、Torch、TensorFlow、MXNet
三、图像底层特征提取
1. 特征提取:边缘和轮廓
- 边缘和轮廓能反映图像的内容。(类似于 素描 )
2. 边缘提取:
- 边缘的定义:是图像中亮度突然变化的区域 / 图像灰度构成的曲面上的陡峭区域 / 像素灰度存在阶跃变化或屋脊状变化的像素的集合
- 为什么要提取边缘?
边缘特征对于图像的变化不敏感:几何变化、灰度变化、光照方向变化
- 对于灰度图像如何提取边缘?
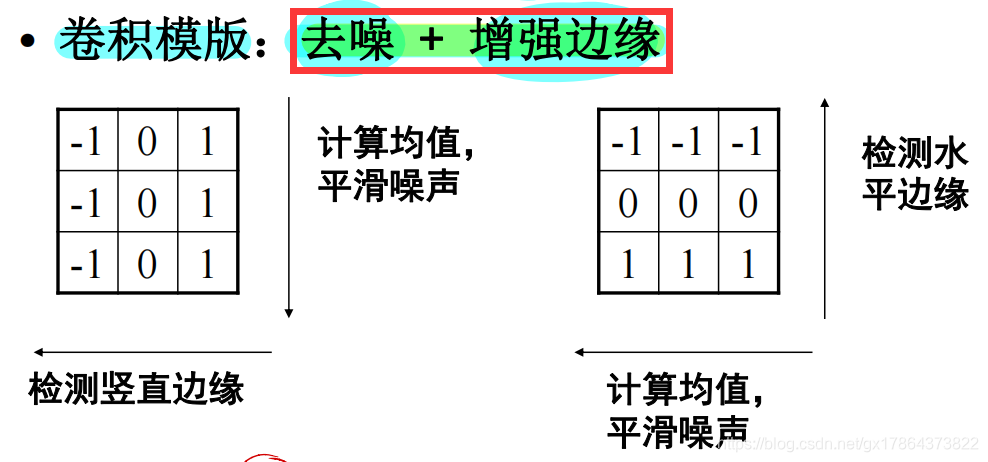
- 抑制噪声:低通滤波(噪声的频率高)、平滑、去噪、模糊
- 边缘特征增强:高通滤波、锐化
- 边缘定位
- 提取边缘的方法
使用微分滤波器提取边缘(微分算子):
- 一阶微分滤波器:梯度算子
- 二阶微分滤波器:LoG
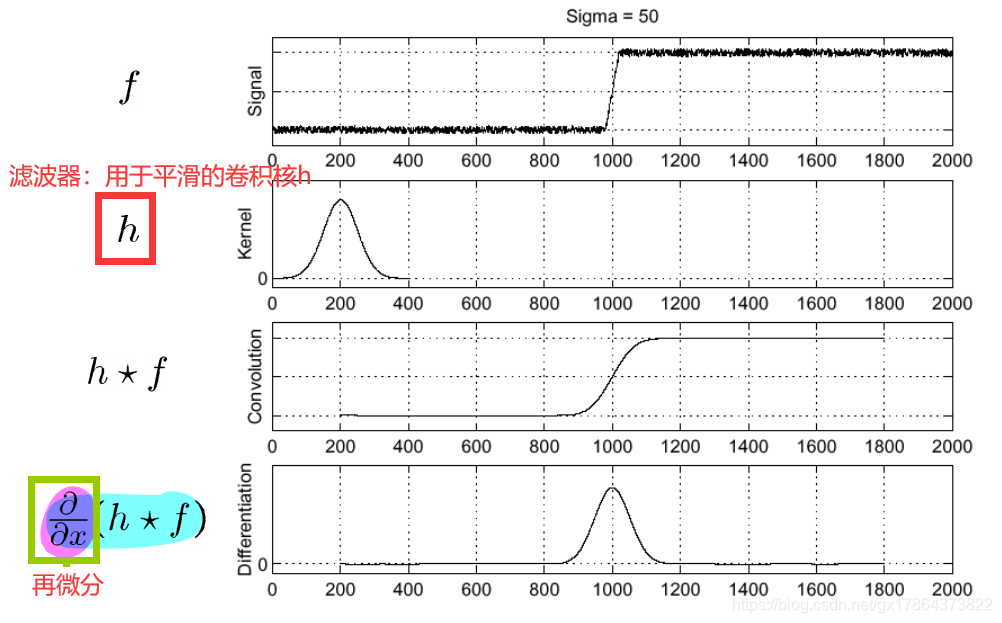
但仅仅直接一阶微分或者二阶微分,噪声的影响太大了。
所以要首先进行滤波。
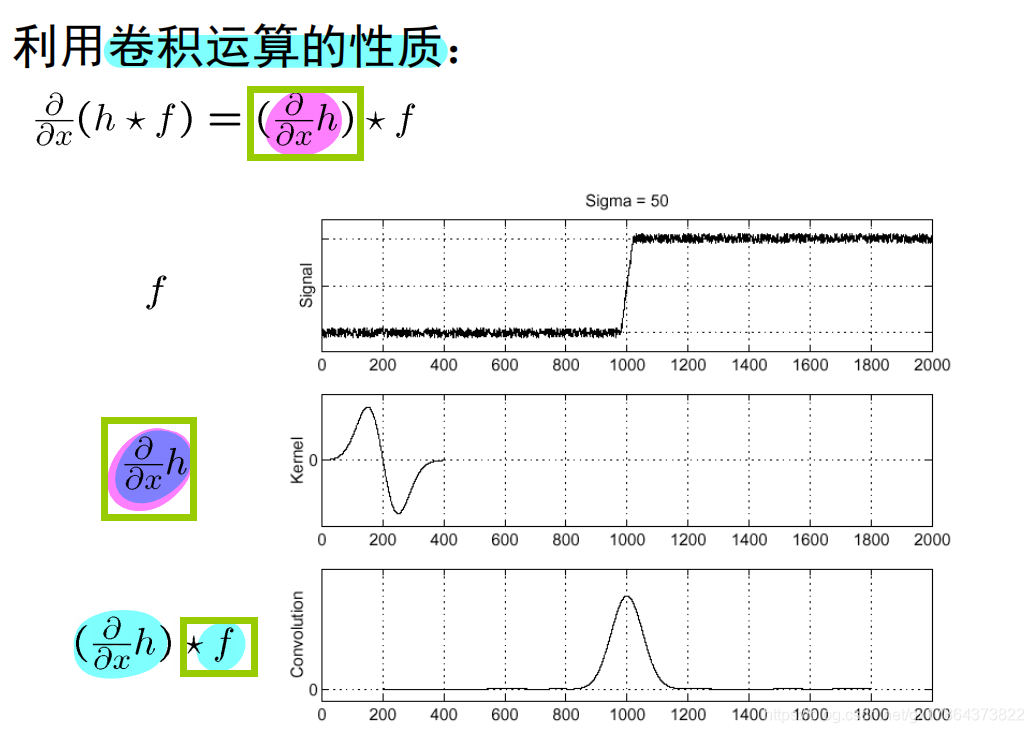
如果再利用 卷积运算的性质,则变为:
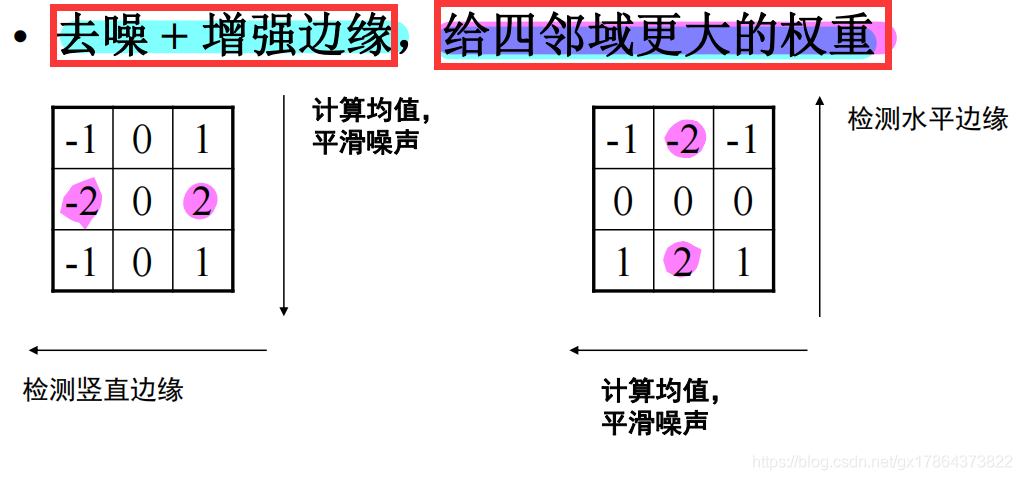
图像梯度算子(在数字图像上计算一阶微分)的近似:Sober算子、Prewitt算子、Roberts算子
- Prewitt算子:近似一阶微分
- Sobel算子:近似一阶微分
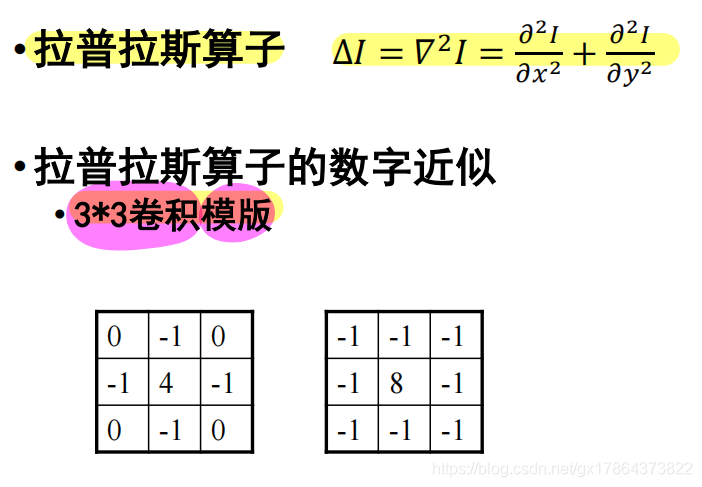
在数字图像上计算二阶微分:
- 拉普拉斯算子的数字近似:3×3卷积模板
- 但!实际中几乎不单独使用拉普拉斯算子。
因为二次求导数对噪声很敏感,所以通常要配合滤波器同时使用 —> LoG。
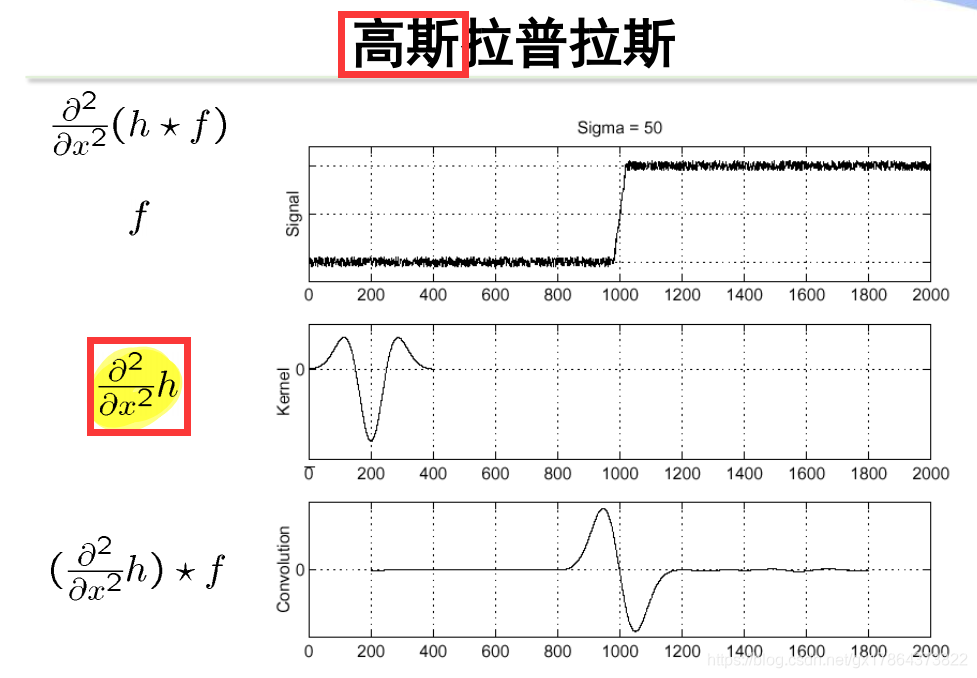
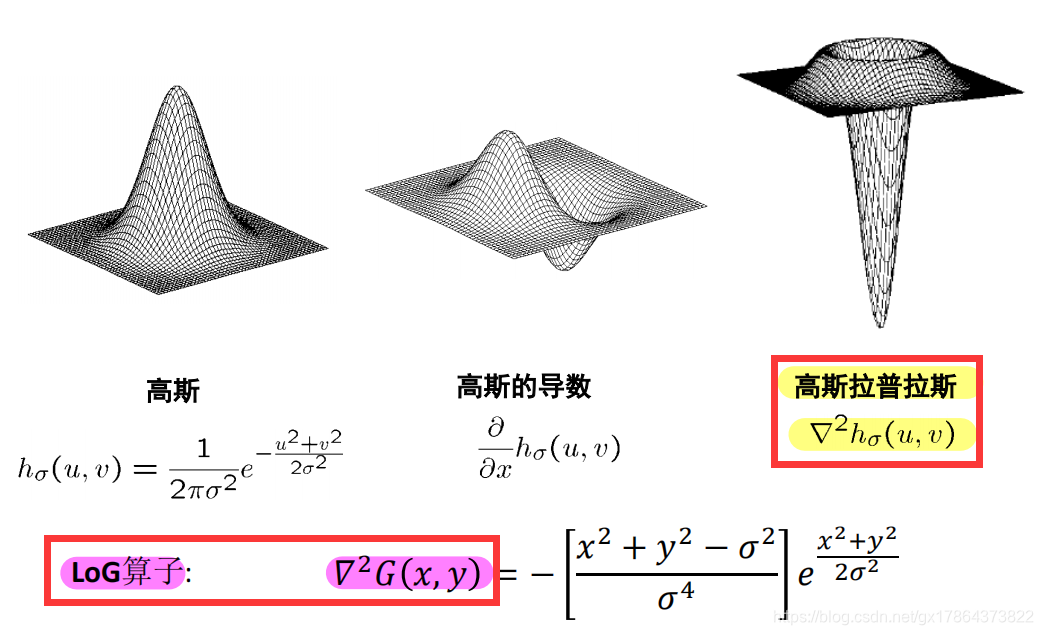
LoG(Laplacian of Gaussian):
- 首先用Gauss函数对图像进行平滑,抑制噪声
- 再对经过平滑的图像使用Laplacian算子
- 利用卷积的性质:LoG算子 = Gaussian算子 + Laplacian二阶微分
二维边缘微分滤波器:
- LoG 也称为 Mexican hat(因为其形状)。
LoG检测到的边缘的特点:
Canny算子:Canny边缘检测器
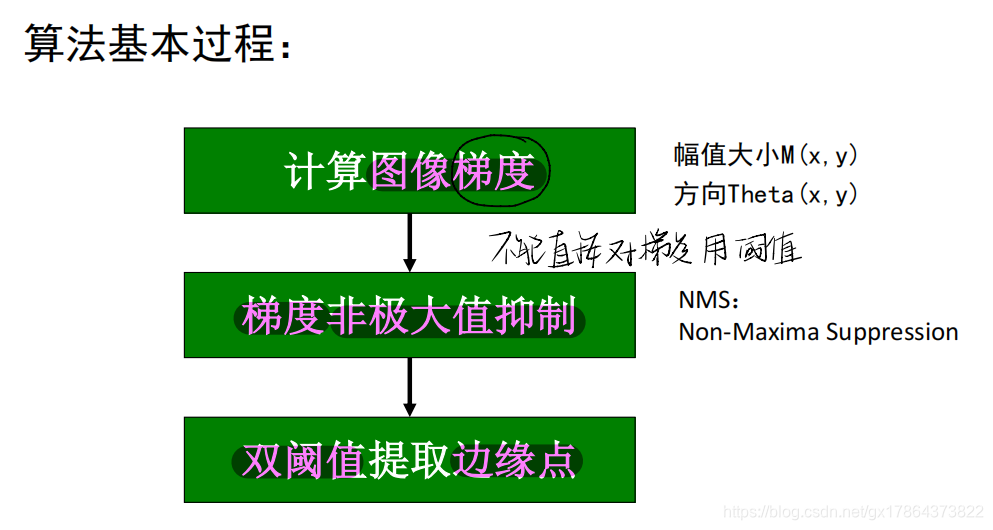
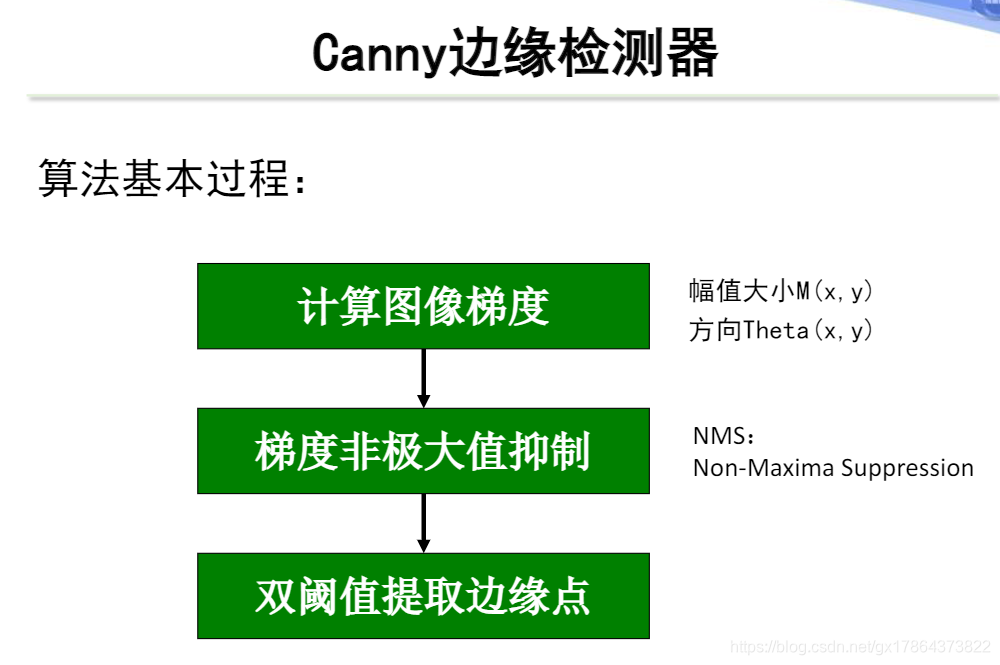
- Canny边缘检测算法的基本过程:计算图像梯度、梯度非极大值抑制、双阈值提取边缘点
Step1:计算图像梯度(高斯函数的一阶导数)
Step2:非极大值抑制NMS(保留梯度方向上的极大值点)
Step3:双阈值提取边缘(对NMS结果 使用阈值 进行 二值化)- 阈值越大,得到的边缘点越少。
Canny算子的优点:参数较少、计算效率、得到的边缘连续完整
参数的选择:Gauss滤波(Canny边缘检测也要先把原始图像进行高斯滤波后再计算其梯度幅值图像)的尺度、双阈值的选择
Canny算子的流程:
- 原始图像
- 原始图像经过高斯平滑
- 梯度幅值图像
- 梯度幅值经过非极大值抑制来二值化图像
- 低阈值边缘图像、高阈值边缘图像
- Canny输出边缘图像
3. 图像特征点提取:
- 提取点特征的作用:运动目标跟踪、物体识别、图像配准、全景图像拼接、三维重建
- 角点定义
- 角点的检测算法:Harris角点、FAST
Harris角点检测的基本思想:
- 从图像的局部小窗口观察图像特征
- 角点定义:窗口内任意方向的移动都导致图像灰度的明显变化
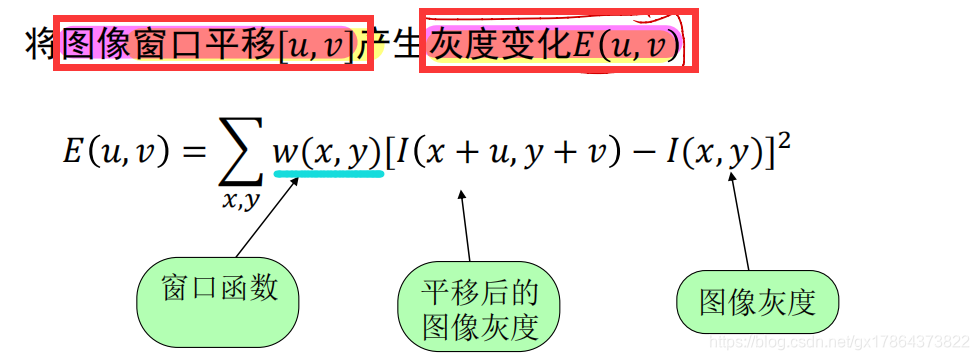
Harris检测的数学表达:
经过对如上公式的泰勒展开等变化,对于局部微小的移动量[u,v],可以近似得到下面的表达:
但此时也并非是通过直接求解E(u,v)的值来判断角点。
是通过对窗口内的像素的x方向上的梯度与y方向上的梯度进行统计分析。
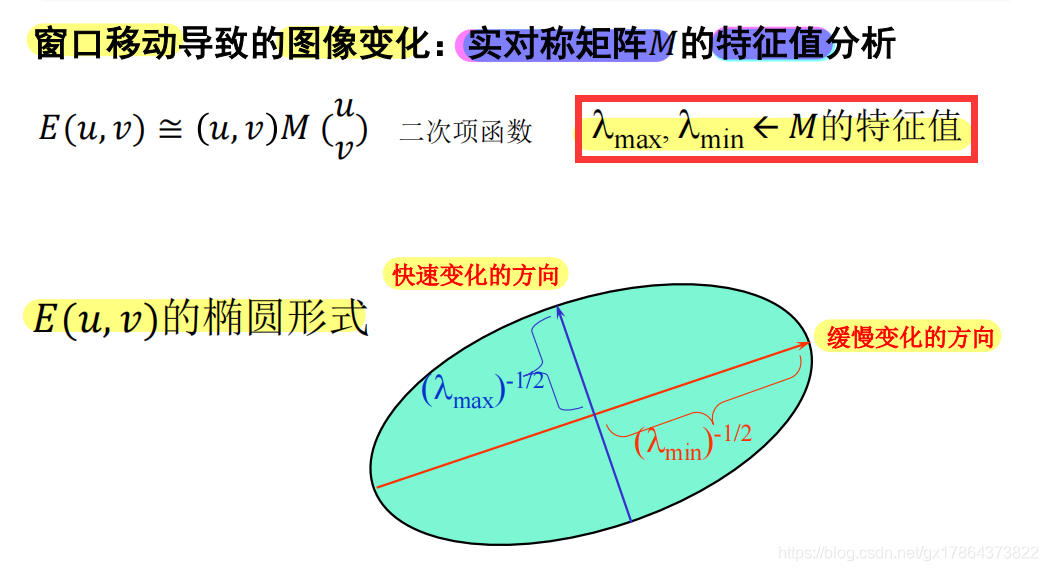
即为对实对称矩阵M进行特征值分析。
总结:
- 统计局部区域的变化,就看梯度分布。
- 所以,怎么更好的去拟合分布呢?用特征值。
- 但怎么更好的描述特征值大或小呢?用角点响应函数R。
对每一个窗口计算得到一个分数R(角点响应函数),根据R的大小来判定窗口内是否存在harris特征角。
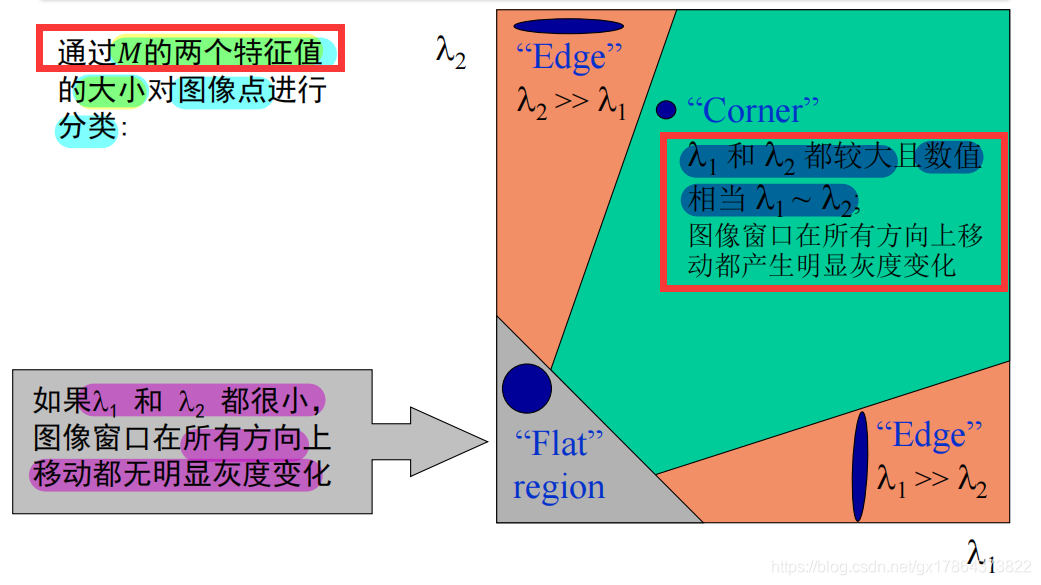
(使用M的特征值表达图像点局部灰度变化的情况,定义角点响应函数R。)
- R只与M的特征值有关。
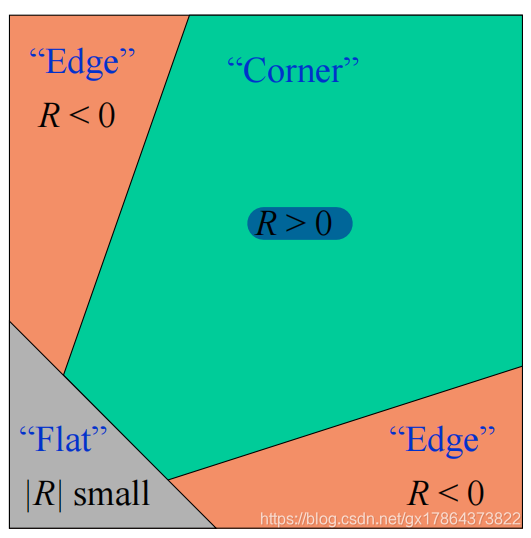
- 角点:R为大数值正数;边缘:R为大数值负数;平坦区:R为小数值。
- 增大k的值,降低角点灵敏度,减少被检测角点的数量。
Harris角点检测算法:
- 对角点响应函数R进行阈值处理:R > threshold
- 提取R的局部极大值
Harris角点的性质:
- 旋转不变性:角点响应函数R对图像的旋转具有不变性
- 对于图像灰度的仿射变化具有部分的不变性
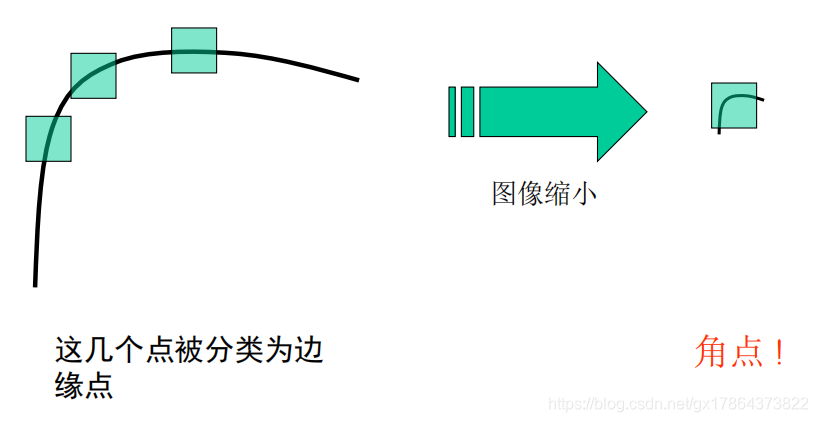
- 对于图像几何尺度变化不具有不变性
FAST(Features from Accelerated Segment Test):
- FAST的假设(不搞小区域):若该点的灰度值比 其周围领域内 足够多的像素点灰度值大或小,则该点可能为角点。
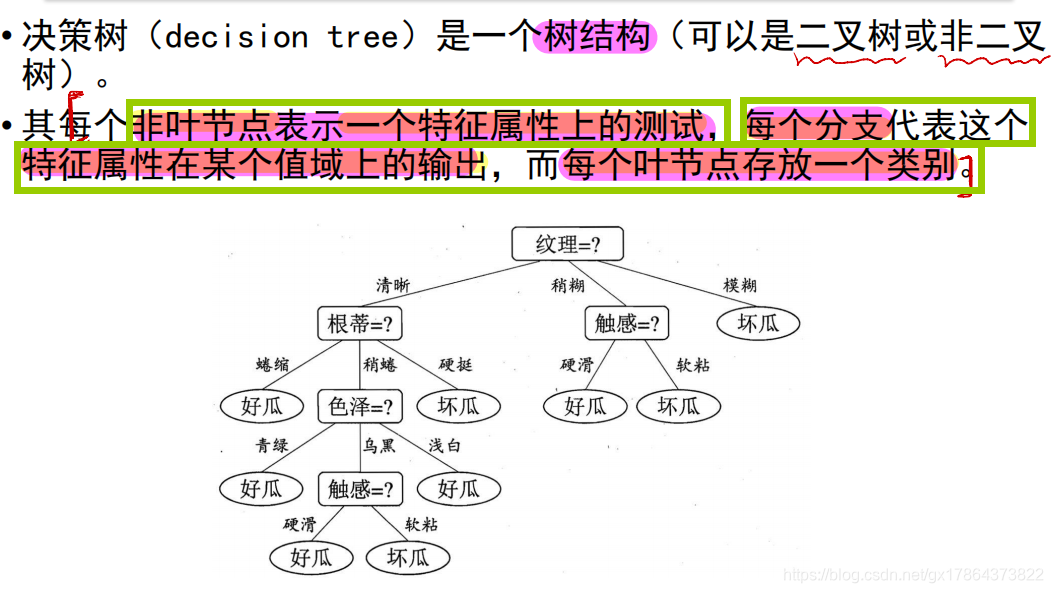
决策树:
- FAST没有尺度不变性和旋转不变性。
老师第二节课提问的问题:
- 以下问题是怎么解决的?

- 局部感受野:某个神经元能看到的输入图像的区域 — 卷积核的大小变化
- 权值共享:降低训练参数
- 卷积
- 池化/下采样:降维、降低平移敏感度
- Canny边缘检测分为几大块?
- 不能直接对梯度用阈值
- 讲讲Harris:
- 统计局部区域的变化:看梯度分布。
- 所以怎么更好的去分布拟合?看特征值

本章节考过的题目:
- 详述Canny边缘检测算法的实现过程
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!