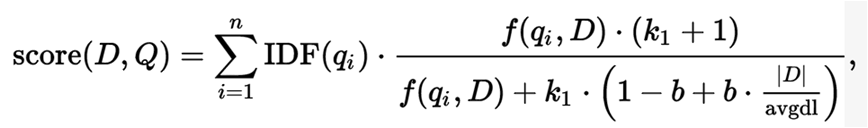Term weight algorithm in IR

1 TF-IDF

2 BM25

f是TD-IDF中的TF，|D|是文档D的长度，avgdl是语料库全部文档的平均长度。k1和b是参数。usually chosen, in absence of an advanced optimization, as $k_1 \in [1.2, 2.0]$ and b = 0.75 。

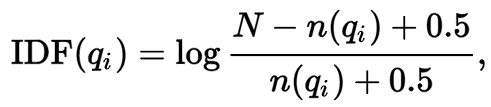
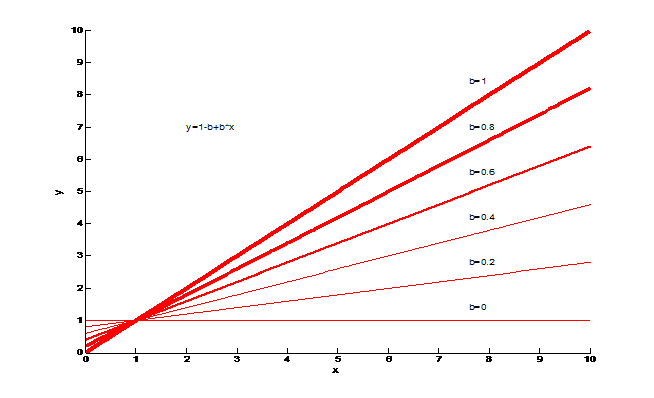
b的相关性

令： y=1-b+b*x， x表示|D|/avgdl, x与y的关系如上图。
b越大，文档长度对相关性得分的影响越大，反之越小。b越大时，当文档长度大于平均长度，那么相关性得分越小；反之越大。
这可以理解为，当文档较长时，包含qi的机会越大，因此，同等fi的情况下，长文档与qi的相关性应该比短文档与qi的相关性弱。

K的相关性

令： y=(tf*(k+1))./(tf+k)， k与y的关系如下图。

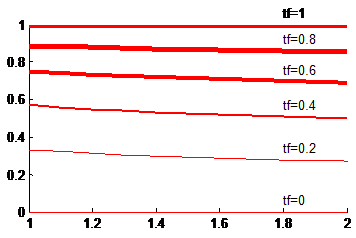
从图表明, k对相似度的影响不大。

3 DFR(divergence form randomness)

Basic Randomness Models

The DFR models are based on this simple idea: “The more the divergence of the within-document term-frequency from its frequency within the collection, the more the information carried by the word t in the document d”. In other words the term-weight is inversely related to the probability of term-frequency within the document d obtained by a model M of randomness:

$$\displaystyle \textrm{weight} (t\vert d) \propto -\log \textrm{Prob}_{M} \left (t\in d\vert\textrm{Collection}\right)$$
(8)
where the subscript M stands for the type of model of randomness employed to compute the probability. The basic models are derived in the following table.

Basic DFR Models
D	Divergence approximation of the binomial
P	Approximation of the binomial
BE	Bose-Einstein distribution
G	Geometric approximation of the Bose-Einstein
I(n)	Inverse Document Frequency model
I(F)	Inverse Term Frequency model
I(ne)	Inverse Expected Document Frequency model

If the model M is the binomial distribution, then the basic model is P and computes the value:

$$\displaystyle -\log \textrm{Prob}_{P}(t\in d\vert \textrm{Collection})=-\log \left(\begin {array}{c} TF\ tf \end{array}\right )p^{tf}q^{TF -tf}$$
where:

• TF is the term-frequency of the term t in the Collection
• tf is the term-frequency of the term t in the document d
• N is the number of documents in the Collection
• p is 1/N and q=1-p

Similarly, if the model M is the geometric distribution, then the basic model is G and computes the value:

$$-log Prob_G(t\in d|Collection)=-log((\frac{1}{1+\lambda})(\frac{\lambda}{1+\lambda}))$$
where λ = F/N.

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！