栈及其应用（表达式求值、括号匹配）

一、栈（stack）

1、栈的特点

  栈(Stack)是一种线性存储结构，它具有如下特点：

【Note】：
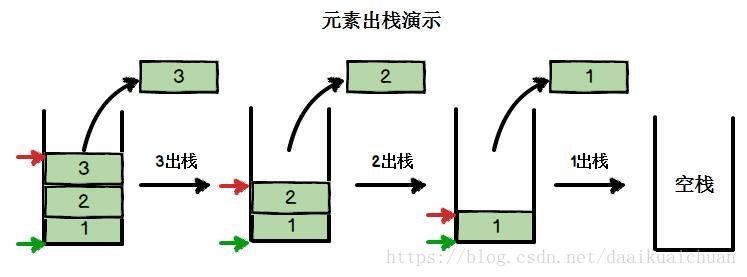
（1）栈中的数据元素遵守”先进后出”(First In Last Out)的原则，简称FILO结构。
（2）限定只能在栈顶进行插入和删除操作。

  栈在计算机中应用相当广泛，包括递归的调用和返回、二叉树和森林的遍历、调用子程序及从子程序返回、表达式的转换和求值、CPU的中断处理等等。

2、栈的相关概念

（1）栈顶（top()）与栈底：允许元素插入与删除的一端称为栈顶，另一端称为栈底。
（2）压栈( push() )：栈的插入操作，叫做进栈，也称压栈、入栈。
（3）弹栈( pop() )：栈的删除操作，也叫做出栈。

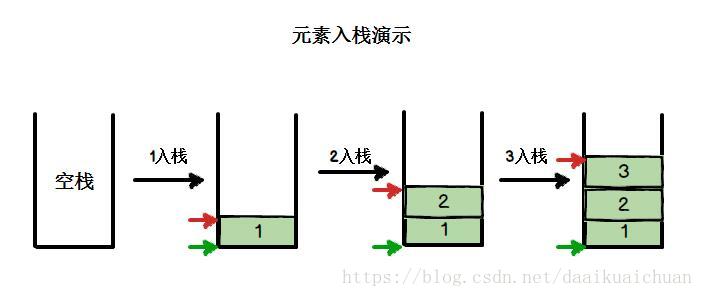
  栈的实现可以使用数组和链表。

二、栈的应用之表达式求值

1、逆波兰表达式简介

  假定给定一个只 包含 加、减、乘、除，和括号的算术表达式，你怎么编写程序计算出其结果。问题是：在表达式中，括号，以及括号的多层嵌套 的使用，运算符的优先级不同等因素，使得一个算术表达式在计算时，运算顺序往往因表达式的内容而定，不具规律性。 这样很难编写出统一的计算指令。
  使用逆波兰算法可以轻松解决。他的核心思想是将普通的中缀表达式转换为后缀表达式。

  转换为后缀表达式的好处是：

• 去除原来表达式中的括号，因为括号只指示运算顺序，不是完成计算必须的元素。

• 使得运算顺序有规律可寻，计算机能编写出代码完成计算。虽然后缀表达式不利于人阅读，但利于计算机处理。

2、将中缀表达式转换成后缀式（逆波兰表达式）

1. 从左到右读进中序表达式的每个字符。

2. 如果读到的字符为操作数，则直接输出到后缀表达式中。

3. 如果遇到“)”，则弹出栈内的运算符，直到弹出到一个“(”,两者相互抵消。

4. “(”的优先级在栈内比任何运算符都小，任何运算符都可以压过它，不过在栈外却是优先级最高者。

5. 当运算符准备进入栈内时，必须和栈顶的运算符比较，如果外面的运算符优先级高于栈顶的运算符的优先级，则压栈；如果优先级低于或等于栈顶的运算符的优先级，则弹栈。直到栈顶的运算符的优先级低于外面的运算符优先级或者栈为空时，再把外面的运算符压栈。

6. 中缀表达式读完后，如果运算符栈不为空，则将其内的运算符逐一弹出，输出到后缀表达式中。

//比较lhs的优先级是否不高于rhs，rhs表示栈顶的符号
bool priority(const char &lhs, const char &rhs)
{if (rhs == '(')//左括号在栈外优先级最高return false;if (lhs == '+' || lhs == '-')return true;if ((lhs == '*' || lhs == '/') && (rhs == '*' || rhs == '/'))return true;return false;
}
//将中缀表达式转换成后缀式（逆波兰表达式）
string exchange(const string &str)
{vector<char> vec;string res;stack<char> st;//操作符堆栈for (int i = 0; i < str.size(); ++i){if (isdigit(str[i]))//如果是数字，直接输出到后序表达式中{vec.push_back(str[i]);}else//如果是符号,需要与栈顶的元素进行比较{if (st.empty() || str[i] == '(')//小括号在栈外优先级最高，直接压栈st.push(str[i]);else{if (str[i] == ')')//遇到右括号，则弹栈，直到遇到左括号，两者相互抵消{while (!st.empty() && st.top() != '('){vec.push_back(st.top());st.pop();}st.pop();}else//遇到的是其他操作符{if (priority(str[i], st.top()))//优先级比栈顶元素低{while (!st.empty()){vec.push_back(st.top());st.pop();}st.push(str[i]);}else//优先级比栈顶元素高，压栈{st.push(str[i]);}}}}}while (!st.empty())//如果堆栈不为空，则将其中的元素全部弹出{vec.push_back(st.top());st.pop();}for (auto v : vec)res += v;return res;
}

3、后缀表达式求值

  后缀表达式具有和前缀表达式类似的好处，没有优先级的问题。

1. 直接读取表达式，如果遇到数字就压栈。

2. 如果遇到运算符，就弹出两个数进行运算，随后再将运算结果压栈。

//定义四则运算
int operate(int first, int second, char op)
{int res = 0;switch (op){case '+':res = first + second;break;case '-':res = first - second;break;case '*':res = first*second;break;case '/':res = first / second;break;default:break;}return res;
}int calculate(string input)
{stack<int> st;//操作数堆栈for (auto &s : input){if (isdigit(s))//如果是数字就压栈{st.push(s - '0');}else//遇到字符就弹出两个操作数进行运算{int a = st.top();st.pop();int b = st.top();st.pop();st.push(operate(b, a, s));}}return st.empty() ? 0 : st.top();//最后的结果为栈顶元素
}

int main(int argc, char const *argv[])
{string str = "1+(3+4)*5-2";cout << exchange(str) << endl;cout << calculate(exchange(str)) << endl;system("pause");return 0;
}

三、栈的应用之括号匹配

  ​括号匹配在很多字符串处理的场景中时常被用到，诸如各大IDE括号不匹配的错误提示，编译器编译时检查应该成对出现的括号是否符合要求等，在这里我们就直接使用一种比较常规，但效率不差的方法去解决括号匹配的问题就行了。

  Description: 给定一个字符串，其中的字符只包含三种括号：花括号{ }、中括号[ ]、圆括号( )，即它仅由 “( ) [ ] { }” 这六个字符组成。设计算法，判断该字符串是否有效，即字符串中括号是否匹配。括号匹配要求括号必须以正确的顺序配对，如“{ [ ] ( ) }” 或 “[ ( { } [ ] ) ]” 等为正确的格式，而 “[ ( ] )” 或 “{ [ ( ) }” 或 “( { } ] )” 均为不正确的格式。

  ​定义一个栈，遇到左括号就压栈，当遇到一个右括号时，首先栈顶元素是否是左括号，如果是的则对栈进行pop操作表明顶部元素已被匹配，否则为不匹配情况，直接返回false。当整个字符串遍历结束，我们就可以通过判断该栈是否为空来判断整个字符串中的符号是否匹配。

  具体代码如下：

#include 
#include 
#include 
using namespace std;
int main(int argc, char const *argv[])
{string str;getline(cin,str);stack<char> st;int l = str.size();int flag = 1;for (int i=0 ; iswitch(str[i]){case '(' : st.push(str[i]) ; break;case '[' : st.push(str[i]) ; break;case '{' : st.push(str[i]) ; break;case ')' : if(st.top() == '(')st.pop();elseflag = 0; break;case ']' : if(st.top() == '[')st.pop();elseflag = 0; break;case '}' : if(st.top() == '{')st.pop();elseflag = 0; break;}}if(!flag){cout << "no" << endl;}else{if(!st.empty()){cout << "no" << endl;}else{cout << "yes" << endl;}}system("pause");return 0;
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！