【图像压缩】有损压缩实现无损预测

updating...

1 绪论

一篇很好的结合对比学习与特征压缩的工作。

本文贡献：

1.公式化面向下游预测任务压缩的概念

2.描述了在增强不变性任务上高表现所需要的比特数。

3.提出无监督目标函数训练压缩器近似最优码率。

4.结合zero-shot方法CLIP，在ImageNet上，减少了1000x的码率。

2 率失真（RD）理论

有损压缩中，通常是的重建。失真有效条件：，形式为的失真，，有限。

3 高预测表现的最小码率

描述保证下游任务高表现表示的最小码率。

论点分三步：1）定义当从中间表示预测下游任务时能够控制下游任务表现的失真项。2）当任务满足不变性条件的时候简化并验证失真项。3）应用RD理论。

3.1 最差预测表现的失真项

所有下游分类任务（是否小狗，是否手写...）：

使用log损失的贝叶斯风险（代表下确界-最小交叉熵，代表原图像，代表某个下游分类任务）：

是中间表示，使用而非预测也对应一个贝叶斯风险。定义最差情况过度风险（worst-case excess risk）（代表上确界）：

如果，则可以实现无损预测：使用和使用的结果相同。使用限定可以确保，

在（2）可以使用之前，有两个问题需要解决：1）不清楚对RD理论而言是否有效；2）最差过度风险假设在所有分类下游任务中取上界，不能枚举实现。

3.2 不变任务

定义1：一组关于等价关系的感兴趣不变任务集，记作，是所有满足的随机变量。

即针对某个数据增强无反应（预测结果相同）的所有下游任务构成。

3.3 不变任务预测的RD理论

关于的最大不变量是满足以下条件的任意函数：

是若干等价类的集合，代表一个下游任务，该下游任务对数据增强具有不变性。图2是示例。

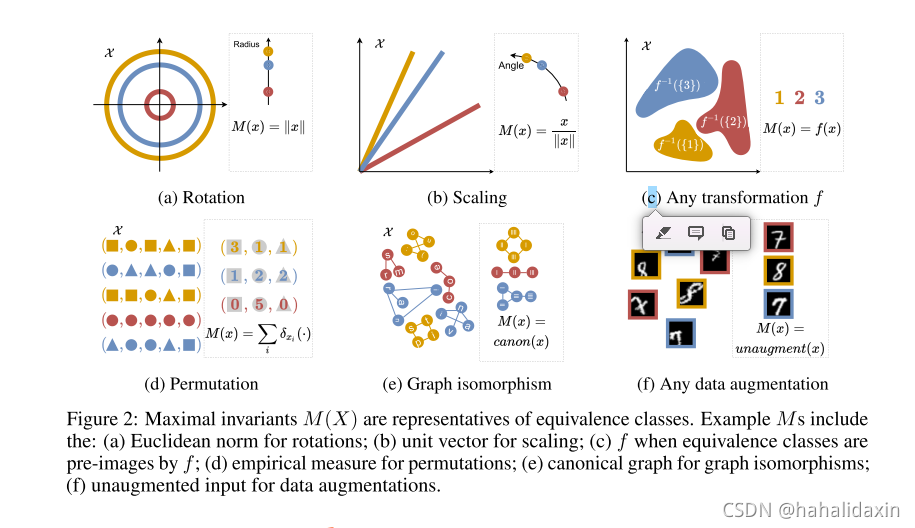
最大不变量去除了对任务而言不变的所有信息（比如a中去除了对任务结果无影响的角度信息），但保留了执行不变性任务所需要的最少信息（如a中的长度信息）。

Appx.B.2证明在弱条件下，存在最大不变任务（则必有最差情况任务），且达到（2）的下确界，简化为从预测的贝叶斯风险，该失真是一个有效失真。于是无需枚举不变任务就可以量化下游表现。

 命题1：等价关系，最大不变量（最多可数多个值），满足，则是一个有效失真项，且。

定理2：（Rate-Invariance）假设条件Prop.1成立，令，代表对于任意都满足的传输需要的最小可达码率。如果则，否则：

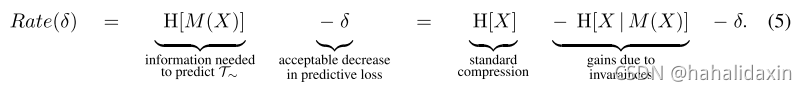
为实现无损预测，需要码率，直觉上来看，这是因为包含了无损预测任意所需要的最小信息。另外，由上式，在所有下游任务log损失表现上减可以节省正好个比特。在右侧，以不同方式分解得到另一种解释：1）对于离散是无损压缩所需要的最少码率，2）是因为期望任务的不变性所减少的信息。如图3。

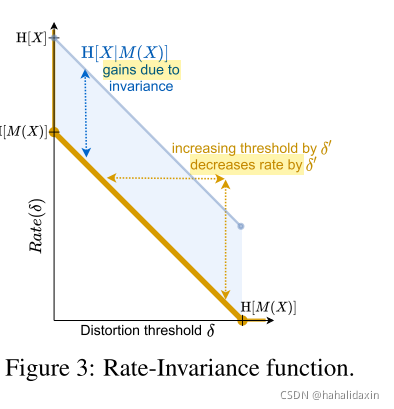
4 不变的神经网络压缩器的无监督训练

目的是找到一个压缩器能够在不变失真项约束下最小化（1）中的RD函数，为了实现这一目的，可以优化以下拉格朗日方程式：

为解决不可用问题，可以把增强图像作为新输入，是的表示，未增强图像作为最大不变任务。与相等，于是可以重写目标函数：

接下来介绍（7）的两种可行的变分界限，可以使用随机梯度下降优化编码器参数。两种优化都使用了标准有损压缩界限，区别在于如何找的上界，第一种使用重建损失，需要由增强图片重建；第二种使用判别损失，尝试辨识哪一个是输入的增强版本。

4.1 变分不变压缩器（Variational Invariant Compressor）

VIC包括编码器，熵模型和解码器，给定数据样本，应用数据增强，压缩得到中间表示，解码器尝试从中间表示重建未增强版本。目标函数：

是熵瓶颈，作为的上界，确保移除不需要的信息。，确保VIC保留不变性任务需要的信息（在代码中使用的mse loss?）。

4.2 瓶颈InfoNCE（BINCE）

第二种无需恢复图像，包括两部分：一个熵瓶颈，一个InfoNCE目标（对比自监督学习）。算法如下：

对每个数据点，数据增强，经过编码器获得中间表示。应用不同增强，送入编码器获得正样本。在中取样n次，应用数据增强，获得n个负样本。共同构成序列。将以上取样过程简化为，引入判别器，目标函数为：

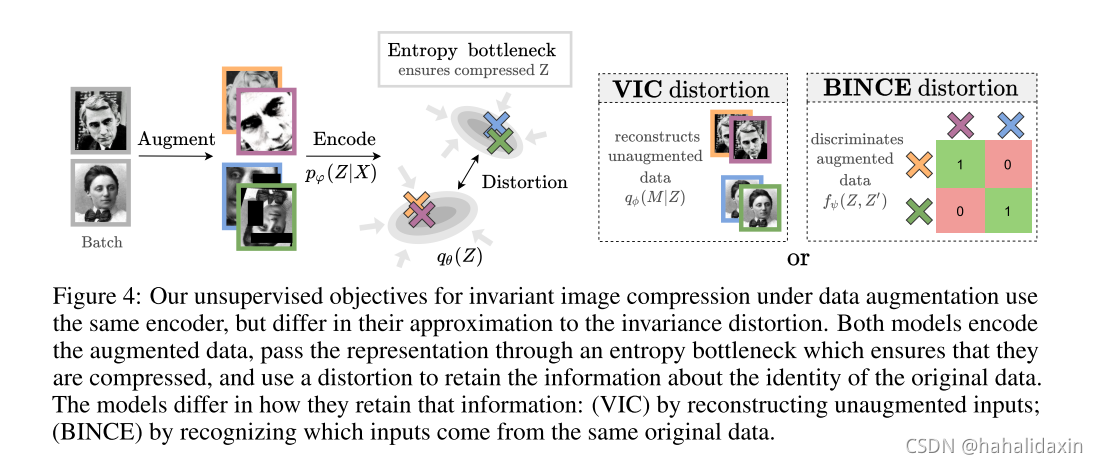
5 实验

关注两个问题:1）框架可以以什么代价达到什么压缩码率2）可以训练一个通用目的的预测编码器吗

5.1 合成简单实验提供视觉直觉

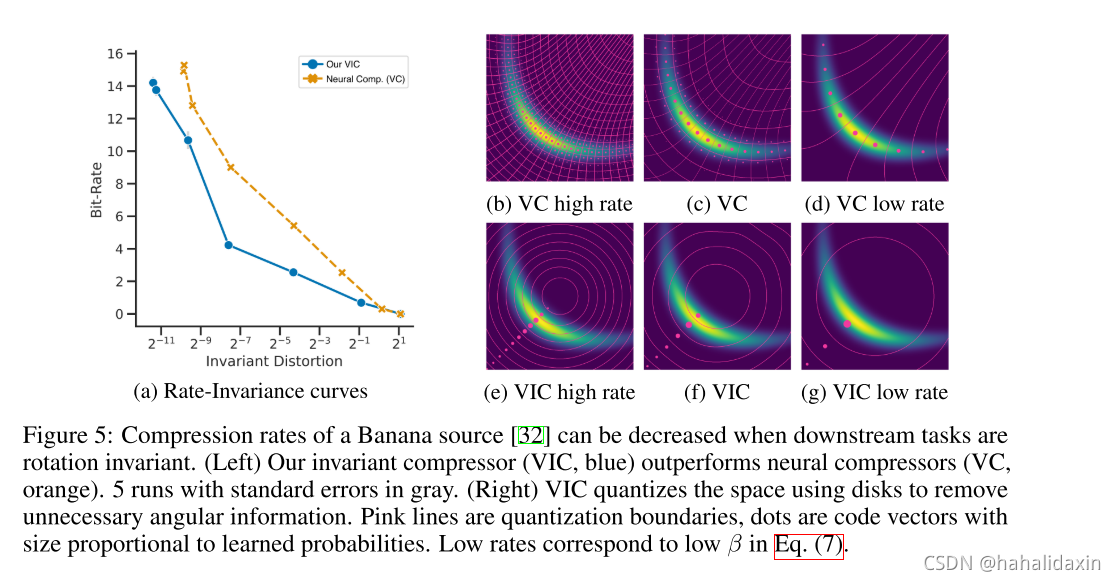
压缩样本来自2维香蕉分布，假设旋转不变性任务为判断一个点是否在单位圆中，比较VC与VIC，两者都使用MSE优化。

码率提升从何而来？对于旋转不变性任务，我们的方法通过学习磁盘形状的量化，丢弃了不必要的角度信息，VIC只保留角度信息，足以将所有随机旋转点映射到最大不变量（粉色点），相比之下，VC企图重构所有图像信息，需要更精细的量化分区。

5.2 对照实验评估

压缩STL10数据集，同时增强（翻转，颜色抖动，裁剪）训练与测试集，保证满足任务不变性的假设。

与标准压缩方法相比BINCE与VIC表现如何？将PNG无损压缩作为baseline，比较下游任务精度与压缩码率。

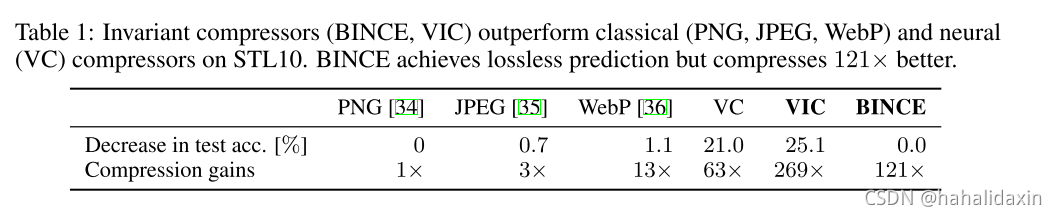
该从表示预测还是重建图像预测？对于VIC，从中间表示而非重建图像预测，提高了9%精确率。这表明不变性重建对于标准图像预测器不是很友好。

增强的分布重要吗？ 50%时间应用增强训练VIC，在测试的时候改变概率，结果相差不大。

5.3 使用预训练自监督模型的一个零次学习（zero-shot）压缩器

CLIP保留了与详细的字幕相关的图像信息，满足，通过一个对比损失，可以保证使用图片表示预测文字表示，反之亦然。这表示CLIP保留了与caption相关的图片的信息，并可能变成一个通用的图像分类压缩器。

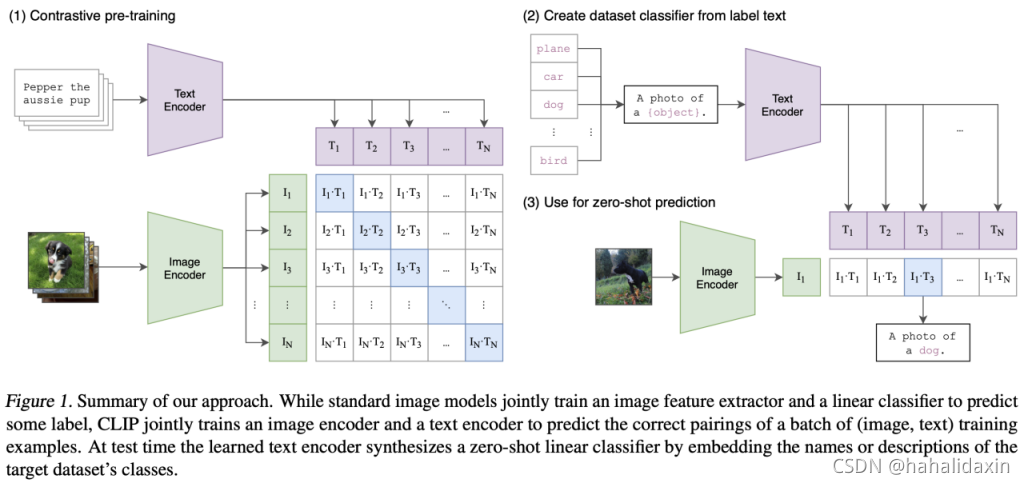
结合BINCE方法，分两步构建新的BINCE压缩器，第一步，下载并固定CLIP参数，第二步，在小数据集MSCOCO上训练一个熵瓶颈压缩CLIP的表示。在8个（不同分类任务，不同图片大小）训练期间未曾谋面（zero-shot）的数据集上测试压缩器。训练策略如下：

可以使用预训练自监督学习获得一个通用压缩器吗？见图2，其中PCam是生物组织数据集。

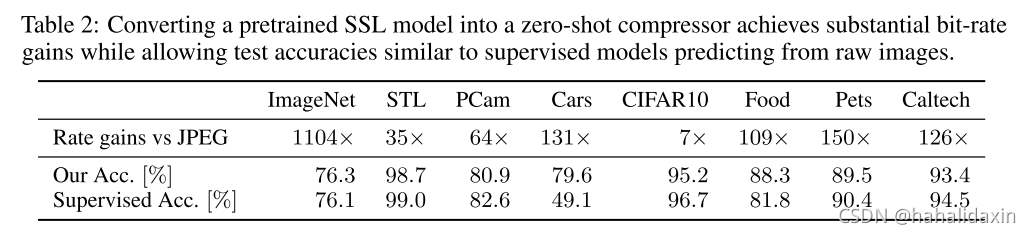
CLIP压缩器保留了所有需要的信息，在这些任务上达到0误差。通过统计训练测试集中压缩表示相同而分类标签不同的样本数以估计过度贝叶斯风险，我们发现在这些数据集上达到了无损预测。

熵瓶颈的作用是什么？比较预训练CLIP，与我们的CLIP压缩器（包含使用不同训练得到的熵瓶颈）。使用低训练熵瓶颈，在没影响预测的情况下平均提升6x码率，提升11x损失不大，高提升16x码率影响开始明显。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！