All mistakes are not equal: Comprehensive Hierarchy Aware Multi-label Predictions (CHAMP)
All mistakes are not equal: Comprehensive Hierarchy Aware Multi-label Predictions (CHAMP)
abstract
这篇论文考虑层级多标签分类(HMC)已存在的问题:每个样本可以存在多个标签;标签基于一颗领域内的层级树。基于所有错误不平等的直觉,我们提出Comprehensive hierarchy aware multi-label predictions(CHAMP),根据层次结构树的严重性对错误预测进行惩罚。基于此的单标签的工作有,而多标签的工作很少,主要原因是没有明确的先验方法来量化多标签设置中错误预测的严重性。多模态(text、audio、image)做实验。
因为没有办法直接量化预测值和真实值之间的距离,所以多标签一直用BCE做loss损失,本论文引入简单的距离公式解决这一问题,且效果提升较多。
preliminaries and problem setting
{ ( x i , y i ) : i = 1 , . . . , n } \{(x_i,y_i):i=1,...,n\} {(xi,yi):i=1,...,n}有标签的训练样本,其中 x i ∈ ∣ R d x_i\in|R^d xi∈∣Rd是输入样本, y i ∈ { 0 , 1 } L y_i\in \{0,1\}^L yi∈{0,1}L是对应的标签向量,L是标签的数量。
τ \tau τ是包含L个节点的层级树
目标是训练一个预测模型 ζ \zeta ζ以x为输入,输出一个L维的向量 y ˉ ∈ [ 0 , 1 ] L \bar y\in[0,1]^L yˉ∈[0,1]L,给定阈值以后,将 y ˉ \bar y yˉ给出最后的输出。
metrics
precision、recall、AUPRC(area under the precision-recall curve)、precison@K、F1@K
介绍几个概念,将会帮助后续量化错误预测的严重性
树上的两个节点 j , j ′ ∈ ∣ L ∣ j,j^{'}\in |L| j,j′∈∣L∣, d i s t ( j , j ′ ) dist(j,j^{'}) dist(j,j′)代表两个节点之间的距离
树上的节点集合 S ⊆ ∣ L ∣ S\subseteq|L| S⊆∣L∣, d i s t ( j , S ) ≡ min j ′ ∈ S d i s t ( j , j ′ ) dist(j,S) \equiv \min_{j^{'}\in S} dist(j,j^{'}) dist(j,S)≡minj′∈Sdist(j,j′)
标签 j ′ j^{'} j′的影响范围是--------没看懂,幸好没影响我后续的理解。。。
method
BCE L x , y ( τ ) = − ∑ j = 1 L { y j log y ˉ j + ( 1 − y j ) log ( 1 − y ˉ j ) } L_{x,y}(\tau)=-\sum_{j=1}^L\{y_j\log\bar y_j+(1-y_j)\log (1-\bar y_j)\} Lx,y(τ)=−∑j=1L{yjlogyˉj+(1−yj)log(1−yˉj)}
修改版的BCE L ~ x , y ( τ ) = − ∑ j = 1 L { y j log y ˉ j + ( 1 + s S ( j ) ) ( 1 − y j ) log ( 1 − y ˉ j ) } \tilde L_{x,y}(\tau)=-\sum_{j=1}^L\{y_j\log\bar y_j+(1+s_S(j))(1-y_j)\log (1-\bar y_j)\} L~x,y(τ)=−∑j=1L{yjlogyˉj+(1+sS(j))(1−yj)log(1−yˉj)},其中S是真实标签 S = { j ′ : y j ′ = 1 } S=\{j^{'}:y_{j^{'}}=1\} S={j′:yj′=1}, s S ( j ) s_S(j) sS(j)代表了标签j的假阳预测的严重性。
给了两种严重性的定义方式:hard 和soft,其中 d i s t m a x = m a x k , k ′ ∈ ∣ L ∣ d i s t ( k , k ′ ) dist_{max}=max_{k,k^{'}\in |L|}dist(k,k^{'}) distmax=maxk,k′∈∣L∣dist(k,k′)
s S h a r d ( j ) = β d i s t ( j , S ) d i s t m a x s_S^{hard}(j)=\beta \frac {dist(j,S)}{dist_{max}} sShard(j)=βdistmaxdist(j,S),只考虑与最近的真实标签的距离
s S s o f t ( j ) = β d i s t h a r m o n i c ( j , S ) d i s t m a x s_S^{soft}(j)=\beta \frac {dist_{harmonic}(j,S)}{dist_{max}} sSsoft(j)=βdistmaxdistharmonic(j,S),考虑所有的真实标签的距离
其中 d i s t h a r m o n i c ( j , S ) = ∣ S ∣ ∑ j ′ ∈ S d i s t ( j , j ′ ) − 1 dist_{harmonic}(j,S)=\frac {|S|}{\sum_{j^{'}\in S}dist(j,j^{'})^{-1}} distharmonic(j,S)=∑j′∈Sdist(j,j′)−1∣S∣
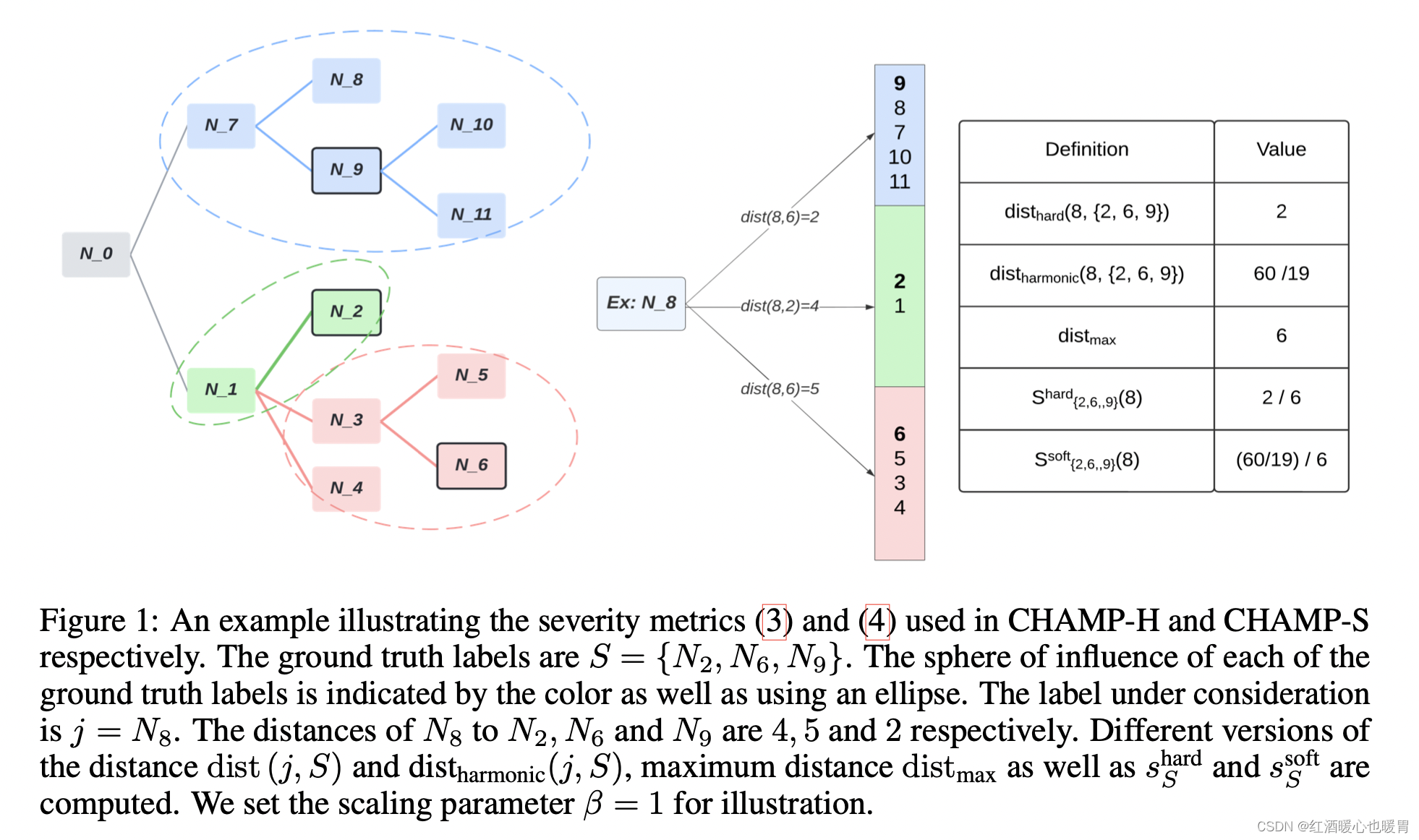
这张图里面不理解不同颜色的圈,但是不影响计算。。
而且右侧dist(8,6)应该是dist(8,9)
真实标签是2、6、9,预测标签是8
8和9的距离是7、9,所以dist(8,9)=2
8和2的距离是7、0、1、2,所以dist(8,2)=4
8和6的距离是7、0、1、3、6,所以dist(8,6)=5,所以 d i s t h a r d ( 8 , { 2 , 6 , 9 } ) = 2 dist_{hard}(8,\{2,6,9\})=2 disthard(8,{2,6,9})=2
最大距离是10与6之间的距离9、7、0、1、3、6,所以 d i s t m a x = 6 dist_{max}=6 distmax=6
这样就可以算出 s { 2 、 6 、 9 } h a r d ( 8 ) = 2 / 6 s^{hard}_{\{2、6、9\}}(8)=2/6 s{2、6、9}hard(8)=2/6
d i s t h a r m o n i c ( j , S ) = 3 1 2 + 1 4 + 1 5 = 60 19 dist_{harmonic}(j,S)=\frac{3}{\frac{1}{2}+\frac{1}{4}+\frac{1}{5}}=\frac {60}{19} distharmonic(j,S)=21+41+513=1960
这样就可以算出 s { 2 、 6 、 9 } s o f t ( 8 ) = ( 60 / 19 ) / 6 s^{soft}_{\{2、6、9\}}(8)=(60/19)/6 s{2、6、9}soft(8)=(60/19)/6
Results
code
论文中提供了tensorflow版本的代码,但是缺少get_distance部分的代码,我按照自己的理解,简单进行了实现
def get_distance(node1, node2, kid2parent):i = 1tmp = [node1, node2]while node1 in dict_kid2parent:i = i + 1node1 = dict_kid2parent[node1]tmp.append(node1)j = 1while node2 in dict_kid2parent:j = j + 1node2 = dict_kid2parent[node2]tmp.append(node2)b = dict(Counter(tmp))num = len([key for key,value in b.items()if value > 1])return i + j - num*2dict_idx2labels = {1:"N_2", 2:'N_3', 3:'N_4', 4:'N_5', 5:'N_6', 6:'N_7', 7:"N_8", 8:"N_9", 9:"N_10", 10:"N_11", 0:"N_1"}
dict_kid2parent = {'N_10':'N_9', 'N_11':'N_9', 'N_9':'N_7', 'N_8':'N_7', "N_5":"N_3", "N_6":"N_3", "N_3":"N_1", "N_4":"N_1", "N_2":"N_1"}
get_distance('N_8', 'N_9', dict_kid2parent)
#2
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!