[Modern Robotics] 2 -旋转与角速度

Modern Robotics

• 旋转矩阵
• • 旋转矩阵与特殊正交群
  • 旋转矩阵的性质
  • 旋转矩阵的使用
• 角速度
• 旋转的指数坐标表示
• • 线性微分方程的一些必要结论
  • 旋转的指数坐标
  • 旋转的矩阵对数

旋转矩阵

旋转矩阵与特殊正交群

在上篇文章中说过，旋转矩阵 $R$ 的9个变量中，只有3个是独立的，这说明矩阵有6个显式的约束。如下条件应满足：
(a) 坐标系的轴 x b ^ , y b ^ , z b ^ \hat{x_b}, \hat{y_b}, \hat{z_b} xb​^​,yb​^​,zb​^​ 应为单位向量：
(3.17) r 11 2 + r 21 2 + r 31 2 = 1 r 12 2 + r 22 2 + r 32 2 = 1 r 13 2 + r 23 2 + r 33 2 = 1 r_{11}^2 + r_{21}^2 + r_{31}^2 = 1 \\ r_{12}^2 + r_{22}^2 + r_{32}^2 = 1 \\ r_{13}^2 + r_{23}^2 + r_{33}^2 = 1 \tag{3.17} r112​+r212​+r312​=1r122​+r222​+r322​=1r132​+r232​+r332​=1(3.17)
(b) 三个坐标轴互相垂直：
(3.18) r 11 r 12 + r 21 r 22 + r 31 r 32 = 0 r 12 r 13 + r 22 r 23 + r 32 r 33 = 0 r 11 r 13 + r 21 r 23 + r 31 r 33 = 0 r_{11}r_{12} + r_{21}r_{22} + r_{31}r_{32} = 0 \\ r_{12}r_{13} + r_{22}r_{23} + r_{32}r_{33} = 0 \\ r_{11}r_{13} + r_{21}r_{23} + r_{31}r_{33} = 0 \tag{3.18} r11​r12​+r21​r22​+r31​r32​=0r12​r13​+r22​r23​+r32​r33​=0r11​r13​+r21​r23​+r31​r33​=0(3.18)
如上的六个约束条件可表示为：
(3.19) R T R = I R^TR = I \tag{3.19} RTR=I(3.19)
其中， R T R^T RT是矩阵转置，$I$ 为单位阵。

同样对于右手旋转矩阵，还有如下性质：
$$detR=1\text{\hspace{1em}(3.21)}$$

所有的 $3\times 3$ 实数矩阵组成了特殊正交群 $SO(3)$，定义如下：满足
(i) R T R = I R^TR = I RTR=I
(ii) $detR=1$

类似的也有特殊正交群 $SO(2)$，对于$R\in SO(2)$，有：
R = [ r 11 r 12 r 21 r 22 ] = [ c o s θ − s i n θ s i n θ c o s θ ] . R = \left[ \begin{matrix} r_{11} & r_{12} \\ r_{21} & r_{22} \end{matrix} \right] = \left[ \begin{matrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{matrix} \right]. R=[r11​r21​​r12​r22​​]=[cosθsinθ​−sinθcosθ​].
其中$\theta \in [0,2\pi )$。$SO(2)$的元素代表的是平面方向，$SO(3)$的元素表示的是空间方向。

旋转矩阵的性质

$SO(2)$ 与 $SO(3)$ 之所以称之为群，是因为他们满足数学上对群的如下定义要求：
(1) 封闭性： $AB$ 也属于群。
(2) 结合律：$(AB)C=A(BC)$
(3) 幺元： 存在单位阵，使$AI=IA=A$
(4) 逆： 群存在 A − 1 A^{-1} A−1，使得 A A − 1 = A − 1 A = I AA^{-1} = A^{-1}A = I AA−1=A−1A=I

并且有如下性质：
(1) 对于任意$R\in SO(3)$，它的逆 R − 1 R^{-1} R−1 也是旋转矩阵，且有 R − 1 = R T R^{-1} = R^T R−1=RT。
(2) 两个旋转矩阵的乘积仍然是旋转矩阵。
(3) 旋转矩阵相乘满足结合律，不满足交换律。
(4) 对于任意向量 x ∈ R 3 ， R ∈ S O ( 3 ) x \in \mathbb{R}^3，R\in SO(3) x∈R3，R∈SO(3)，向量 $y=Rx$ 与 $x$ 有相同的长度或模。

旋转矩阵的使用

对于一个旋转矩阵$R$，有三个主要用处：
(1) 描述一个方向
(2) 改变一个向量或坐标系的参考坐标系
(3) 旋转一个向量或坐标系

对于第一种情况，$R$ 矩阵用来描述一个坐标系。对于第二种，第三种情况，$R$ 矩阵认为是一个操作，作用于一个向量或坐标系（改变其参考坐标系或者旋转它）。

如图3.7所示， { a } \{a\} {a}， { b } \{b\} {b}， { c } \{c\} {c} 坐标系有相同的原点，图示用来说明方向。假设 { a } \{a\} {a} 坐标系与 { s } \{s\} {s} 坐标系是重合的。则此三个坐标系相对于 { s } \{s\} {s} 的方向可表示为：
R a = [ 1 0 0 0 1 0 0 0 1 ] ， R b = [ 0 − 1 0 1 0 0 0 0 1 ] ， R c = [ 0 − 1 0 0 0 − 1 1 0 0 ] R_a = \left[ \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 &1 \end{matrix} \right]， R_b = \left[ \begin{matrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 &1 \end{matrix} \right]， R_c = \left[ \begin{matrix} 0 & -1 & 0 \\ 0 & 0 & -1 \\ 1 & 0 &0 \end{matrix} \right] Ra​=⎣⎡​100​010​001​⎦⎤​，Rb​=⎣⎡​010​−100​001​⎦⎤​，Rc​=⎣⎡​001​−100​0−10​⎦⎤​
对于空间一个 $p$ 点，其在三个坐标系中的坐标为：
p a = [ 1 1 0 ] ， p b = [ 1 − 1 0 ] ， p c = [ 0 − 1 − 1 ] . p_a = \left[ \begin{matrix} 1 \\ 1 \\ 0 \end{matrix} \right]， p_b = \left[ \begin{matrix} 1 \\ -1 \\ 0 \end{matrix} \right]， p_c = \left[ \begin{matrix} 0 \\ -1 \\ -1 \end{matrix} \right]. pa​=⎣⎡​110​⎦⎤​，pb​=⎣⎡​1−10​⎦⎤​，pc​=⎣⎡​0−1−1​⎦⎤​.
同时注意到， { b } \{b\} {b} 是 { a } \{a\} {a} 绕着 z a ^ \hat{z_a} za​^​ 旋转90°得到的， { c } \{c\} {c} 是绕着 { b } \{b\} {b}坐标系的 y b ^ \hat{y_b} yb​^​ 旋转 -90°得到的。

(1) 描述方向
当我们描述 R c R_c Rc​ 时，默认的是 { c } \{c\} {c} 相对于 { s } \{s\} {s} 的方向。为突出相对性，写成 R s c R_{sc} Rsc​。
例如：
R a c = [ 0 − 1 0 0 0 − 1 1 0 0 ] ， R c a = [ 0 0 1 − 1 0 0 0 − 1 0 ] R_{ac} = \left[ \begin{matrix} 0 & -1 & 0 \\ 0 & 0 & -1 \\ 1 & 0 &0 \end{matrix} \right]， R_{ca} = \left[ \begin{matrix} 0 & 0 & 1 \\ -1 & 0 & 0 \\ 0 & -1 &0 \end{matrix} \right] Rac​=⎣⎡​001​−100​0−10​⎦⎤​，Rca​=⎣⎡​0−10​00−1​100​⎦⎤​
简单的计算发现， R a c R c a = I R_{ac}R_{ca} = I Rac​Rca​=I，这说明 R a c = R c a − 1 R_{ac} = R_{ca}^{-1} Rac​=Rca−1​，又根据旋转矩阵的性质，有 R a c = R c a T R_{ac} = R_{ca}^{T} Rac​=RcaT​。事实上，对于任意的两个坐标系 { d } \{d\} {d}, { e } \{e\} {e}，
R d e = R e d − 1 = R e d T R_{de} = R_{ed}^{-1} = R_{ed}^T Rde​=Red−1​=RedT​

(2) 改变参考坐标系
旋转矩阵 R a b R_{ab} Rab​ 描述的是 { b } \{b\} {b} 坐标系在 { a } \{a\} {a}中的方向， R b c R_{bc} Rbc​ 描述的是 { c } \{c\} {c} 坐标系在 { b } \{b\} {b}中的方向，直接计算可得到：
(3.22) R a c = R a b R b c R_{ac} = R_{ab}R_{bc} \tag{3.22} Rac​=Rab​Rbc​(3.22)
这里可以把 R a b R_{ab} Rab​ 看作一个数学操作，把 { c } \{c\} {c}的参考坐标系从 { b } \{b\} {b} 改为 { a } \{a\} {a}。
下标去除规则可帮助我们记住这个性质：
R a b R b c = R a b / R b / c = R a c R_{ab}R_{bc} = R_{a{b\mkern-7mu/}}R_{{b\mkern-7mu/c}} =\quad R_{ac} Rab​Rbc​=Rab/​Rb/c​=Rac​
一个旋转矩阵是由三个单位向量组成的集合，于是一个向量的参考坐标系也可以通过旋转矩阵来改变：
R a b p b = R a b / p b / = p a R_{ab}p_{b} = R_{a{b\mkern-7mu/}}p_{{b\mkern-7mu/}} = \quad p_{a} Rab​pb​=Rab/​pb/​=pa​

(3) 旋转一个向量或坐标系
图3.8展示了一个坐标系 { c } \{c\} {c}，其最初与 { s } \{s\} {s} 坐标系一致。如果我们将 { c } \{c\} {c} 坐标系绕着 w ^ \hat{w} w^ 单位轴旋转$\theta$ 角度，得到 { c ′ } \{c'\} {c′}坐标系，其坐标轴为 x ′ ^ , y ′ ^ , z ′ ^ {\hat{x'}, \hat{y'}, \hat{z'}} x′^,y′^​,z′^。旋转矩阵为 R = R s c ′ R = R_{sc'} R=Rsc′​，代表了 { c ′ } \{c'\} {c′} 的原点相对于 { s } \{s\} {s} 的方向。我们换个角度，也可以认为这个旋转使得 { s } \{s\} {s}变到 { c ′ } \{c'\} {c′}。我们看待旋转矩阵的角度转变成一个操作，而不是方向了，写成：
R = R o t ( w ^ , θ ) R = Rot(\hat{w}, \theta) R=Rot(w^,θ)

典型的绕坐标轴旋转的矩阵如下：
R o t ( x ^ , θ ) = [ 1 0 0 0 c o s θ − s i n θ 0 s i n θ c o s θ ] ， R o t ( y ^ , θ ) = [ c o s θ 0 s i n θ 0 1 0 − s i n θ 0 c o s θ ] ， R o t ( z ^ ， θ ) = [ c o s θ − s i n θ 0 s i n θ c o s θ 0 0 0 1 ] . Rot(\hat{x}, \theta) = \left[ \begin{matrix} 1 & 0 & 0 \\ 0 & cos\theta & -sin\theta \\ 0 & sin\theta &cos\theta \end{matrix} \right]， Rot(\hat{y}, \theta) = \left[ \begin{matrix} cos\theta & 0 & sin\theta \\ 0 & 1 & 0 \\ -sin\theta & 0 &cos\theta \end{matrix} \right]， Rot(\hat{z}，\theta) = \left[ \begin{matrix} cos\theta& -sin\theta & 0 \\ sin\theta & cos\theta & 0 \\ 0 & 0 & 1 \end{matrix} \right]. Rot(x^,θ)=⎣⎡​100​0cosθsinθ​0−sinθcosθ​⎦⎤​，Rot(y^​,θ)=⎣⎡​cosθ0−sinθ​010​sinθ0cosθ​⎦⎤​，Rot(z^，θ)=⎣⎡​cosθsinθ0​−sinθcosθ0​001​⎦⎤​.

更一般的，对于 w ^ = ( w 1 ^ , w 2 ^ , w 3 ^ ) \hat{w} = (\hat{w_1}, \hat{w_2}, \hat{w_3}) w^=(w1​^​,w2​^​,w3​^​)，有：
R o t ( w ^ , θ ) = [ c θ + w 1 ^ 2 ( 1 − c θ ) w 1 ^ w 2 ^ ( 1 − c θ ) − w 3 ^ s θ w 1 ^ w 3 ^ ( 1 − c θ ) + w 2 ^ s θ w 1 ^ w 2 ^ ( 1 − c θ ) + w 3 ^ s θ c θ + w 2 ^ 2 ( 1 − c θ ) w 2 ^ w 3 ^ ( 1 − c θ ) − w 1 ^ s θ w 1 ^ w 3 ^ ( 1 − c θ ) − w 2 ^ s θ w 2 ^ w 3 ^ ( 1 − c θ ) + w 1 ^ s θ c θ + w 3 ^ 2 ( 1 − c θ ) ] Rot(\hat{w}, \theta) = \left[ \begin{matrix} c_\theta+\hat{w_1}^2(1-c_\theta) & \hat{w_1}\hat{w_2}(1-c_\theta) - \hat{w_3}s_\theta & \hat{w_1}\hat{w_3}(1-c_\theta) + \hat{w_2}s_\theta \\ \hat{w_1}\hat{w_2}(1-c_\theta) + \hat{w_3}s_\theta & c_\theta+\hat{w_2}^2(1-c_\theta) & \hat{w_2}\hat{w_3}(1-c_\theta) - \hat{w_1}s_\theta \\ \hat{w_1}\hat{w_3}(1-c_\theta) - \hat{w_2}s_\theta & \hat{w_2}\hat{w_3}(1-c_\theta) + \hat{w_1}s_\theta & c_\theta+\hat{w_3}^2(1-c_\theta) \end{matrix} \right] Rot(w^,θ)=⎣⎡​cθ​+w1​^​2(1−cθ​)w1​^​w2​^​(1−cθ​)+w3​^​sθ​w1​^​w3​^​(1−cθ​)−w2​^​sθ​​w1​^​w2​^​(1−cθ​)−w3​^​sθ​cθ​+w2​^​2(1−cθ​)w2​^​w3​^​(1−cθ​)+w1​^​sθ​​w1​^​w3​^​(1−cθ​)+w2​^​sθ​w2​^​w3​^​(1−cθ​)−w1​^​sθ​cθ​+w3​^​2(1−cθ​)​⎦⎤​
其中， s θ = s i n θ , c θ = c o s θ s_\theta = sin\theta, c_\theta = cos\theta sθ​=sinθ,cθ​=cosθ。对于任意的$R\in SO(3)$ 可以通过单位阵绕着某个 w ^ \hat{w} w^ 旋转 $\theta$ 角度得到。并且有 R o t ( w ^ , θ ) = R o t ( − w ^ , − θ ) Rot(\hat{w},\theta) = Rot(-\hat{w}, -\theta) Rot(w^,θ)=Rot(−w^,−θ)。

现在， R s b R_{sb} Rsb​ 表示的是 { b } \{b\} {b} 相对于 { s } \{s\} {s} 的方向，我们想要将 { b } \{b\} {b} 绕着一个单位轴 w ^ \hat{w} w^ 旋转$\theta$ 角度，如 R = R o t ( w ^ , θ ) R = Rot(\hat{w}, \theta) R=Rot(w^,θ)。为了区分清楚，我们需要指定 w ^ \hat{w} w^ 是相对于 { s } \{s\} {s}的坐标还是相对于 { b } \{b\} {b}的坐标。设 { b ′ } \{b'\} {b′} 坐标系是绕 w s ^ = w ^ \hat{w_s} = \hat{w} ws​^​=w^ 旋转$\theta$ 角得到的新坐标系，且旋转轴 w ^ \hat{w} w^ 是在 { s } \{s\} {s} 坐标下。设 { b ′ ′ } \{b''\} {b′′} 是绕 w b ^ = w ^ \hat{w_b} = \hat{w} wb​^​=w^ 旋转$\theta$ 角得到的新坐标系，且旋转轴 w ^ \hat{w} w^ 是在 { b } \{b\} {b} 坐标下。则有：
R s b ′ = R R s b R s b ′ ′ = R s b R R_{sb'} = RR_{sb} \\ R_{sb''} = R_{sb}R Rsb′​=RRsb​Rsb′′​=Rsb​R
另外，把 R = R o t ( w ^ , θ ) R = Rot(\hat{w}, \theta) R=Rot(w^,θ) 乘在前面，产生了绕 { s } \{s\} {s} 中的 w ^ \hat{w} w^ 旋转，与之相反的是产生了绕 { b } \{b\} {b} 中的 w ^ \hat{w} w^的旋转。见图3.9。

对于旋转一个向量 $v$，需要注意的是只会涉及一个坐标系，在表示 $v$ 向量坐标的坐标系中， w ^ \hat{w} w^ 也同样在这个坐标系中。于是有：
v ′ = R v v' = Rv v′=Rv

角速度

如图3.10所示，假设有一个坐标系 { x ^ , y ^ , z ^ } \{\hat{x}, \hat{y}, \hat{z}\} {x^,y^​,z^} 固定于旋转刚体上， x ^ , y ^ , z ^ \hat{x}, \hat{y}, \hat{z} x^,y^​,z^ 均为单位向量。先从 x ^ ˙ \dot{\hat{x}} x^˙ 开始，当前只有 x ^ \hat{x} x^ 轴的方向可以随着时间变化。如果我们对时间 $t$ 到$t+\Delta t$ 的刚体考察，整个坐标系的改变可以认为是绕着通过坐标系原点的某根单位轴 w ^ \hat{w} w^ 旋转了 $\Delta \theta$。

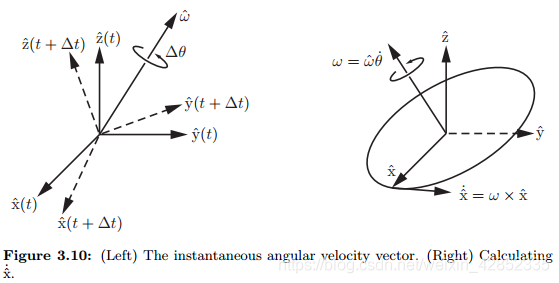
当$\Delta t$ 趋近于0时，$\Delta \theta /\Delta t$ 便变成了旋转的变化率 θ ˙ \dot{\theta} θ˙，且 w ^ \hat{w} w^ 可以认为是瞬时的旋转轴。事实上， w ^ \hat{w} w^ 与 θ ˙ \dot{\theta} θ˙ 可以结合起来表达角速度：
(3.25) w = w ^ θ ˙ w = \hat{w}\dot{\theta} \tag{3.25} w=w^θ˙(3.25)
参照图3.10(b)，有：
x ^ ˙ = w × x ^ y ^ ˙ = w × y ^ z ^ ˙ = w × z ^ \dot{\hat{x}} = w \times \hat{x} \\ \dot{\hat{y}} = w \times \hat{y} \\ \dot{\hat{z}} = w \times \hat{z} x^˙=w×x^y^​˙​=w×y^​z^˙=w×z^
为了表达这些等式，我们需要选择一个表述 $w$ 的坐标系。我们可以选择任何坐标系，但是有两个自然的旋转， { s } \{s\} {s} 与 { b } \{b\} {b}。

(a) 先从固定坐标系 { s } \{s\} {s} 开始。
使$R(t)$作为 $t$ 时刻刚体坐标系相对于固定坐标系的方向。 R ˙ ( t ) \dot{R}(t) R˙(t) 是其随时间的变化率。$R(t)$ 的第一列，记为 r 1 ( t ) r_1(t) r1​(t)，描述了 x ^ \hat{x} x^ 在固定坐标系中的方向，同理 r 2 ( t ) ， r 3 ( t ) r_2(t)， r_3(t) r2​(t)，r3​(t) 描述了
y ^ ， z ^ \hat{y}， \hat{z} y^​，z^ 在固定坐标系中的方向。在某个特定时刻 $t$，在固定坐标系下的角速度 w s ∈ R 3 w_s \in \mathbb{R}^3 ws​∈R3，则有：
r i ˙ = w s × r i , i = 1 , 2 , 3. \dot{r_i} = w_s \times r_i, \quad i=1,2,3. ri​˙​=ws​×ri​,i=1,2,3.
写成矩阵形式：
(3.29) R ˙ = [ w s × r 1 w s × r 2 w s × r 3 ] = w s × R \dot{R} = \left[ \begin{matrix} w_s \times r_1 & w_s \times r_2 & w_s \times r_3 \end{matrix} \right] = w_s \times R \tag{3.29} R˙=[ws​×r1​​ws​×r2​​ws​×r3​​]=ws​×R(3.29)
为了去除等式右边的叉积，介绍一种新记法， w s × R w_s \times R ws​×R 等同于 [ w s ] R [w_s]R [ws​]R，其中 [ w s ] [w_s] [ws​] 是 w s ∈ R 3 w_s \in \mathbb{R}^3 ws​∈R3 的反对称矩阵表达。

有如下定义，给定一个向量 x = [ x 1 , x 2 , x 3 ] T ∈ R 3 x = [x_1,x_2, x_3]^T \in \mathbb{R}^3 x=[x1​,x2​,x3​]T∈R3, 定义
[ x ] = [ 0 − x 3 x 2 x 3 0 − x 1 − x 2 x 1 0 ] [x] = \left[ \begin{matrix} 0 & -x_3 & x_2 \\ x_3 & 0 & -x_1 \\ -x_2 & x_1 & 0 \end{matrix} \right] [x]=⎣⎡​0x3​−x2​​−x3​0x1​​x2​−x1​0​⎦⎤​
$[x]$ 矩阵是一个$3\times 3$ 的反对称矩阵，即：
[ x ] = − [ x ] T [x] = -[x]^T [x]=−[x]T
$3\times 3$ 的实反对称阵集合称作 $so(3)$。

定理
给定任意 w ∈ R 3 ， R ∈ S O ( 3 ) w \in \mathbb{R}^3，R \in SO(3) w∈R3，R∈SO(3)，下列等式成立：
(3.31) R [ w ] R T = [ R w ] R[w] R^T = [Rw] \tag{3.31} R[w]RT=[Rw](3.31)

有了反对称矩阵的表示，重写式(3.29)如下：
(3.33) [ w s ] R = R ˙ [w_s]R = \dot{R} \tag{3.33} [ws​]R=R˙(3.33)
两边右乘 R − 1 R^{-1} R−1，有：
(3.34) [ w s ] = R ˙ R − 1 [w_s] = \dot{R}R^{-1} \tag{3.34} [ws​]=R˙R−1(3.34)

(b) 下面使 w b w_b wb​ 作为 $w$ 在刚体坐标系中的坐标表达。
w s w_s ws​ 与 w b w_b wb​ 是同一个角速度 $w$ 在不同坐标系下的向量表示，依据下标消除原则，且有 w s = R s b w b w_s = R_{sb}w_b ws​=Rsb​wb​：
(3.35) w b = R s b − 1 w s = R − 1 w s = R T w s w_b = R_{sb}^{-1}w_s = R^{-1}w_s = R^Tw_s \tag{3.35} wb​=Rsb−1​ws​=R−1ws​=RTws​(3.35)
用反对称阵表示：
(3.36) [ w b ] = [ R T w s ] = R T [ w s ] R = R T ( R ˙ R T ) R = R T R ˙ = R − 1 R ˙ [w_b] = [R^Tw_s] =R^T[w_s]R =R^T(\dot{R}R^T)R =R^T\dot{R} =R^{-1}\dot{R} \tag{3.36} [wb​]=[RTws​]=RT[ws​]R=RT(R˙RT)R=RTR˙=R−1R˙(3.36)
总体来说，用$R(t)$ 表示相对于固定坐标系的坐标系方向，旋转的坐标系的角速度为$w$，有：
R ˙ R − 1 = [ w s ] R − 1 R ˙ = [ w b ] \dot{R}R^{-1} = [w_s] \\ R^{-1}\dot{R} = [w_b] R˙R−1=[ws​]R−1R˙=[wb​]
其中， w s ∈ R 3 w_s \in \mathbb{R}^3 ws​∈R3 是 $w$ 在固定坐标系下的向量坐标表示， [ w s ] ∈ s o ( 3 ) [w_s] \in so(3) [ws​]∈so(3) 是它的 $3\times 3$ 矩阵表示， w b ∈ R 3 w_b \in \mathbb{R}^3 wb​∈R3 是 $w$ 在刚体坐标系下的向量坐标表示， [ w b ] ∈ s o ( 3 ) [w_b] \in so(3) [wb​]∈so(3) 是它的 $3\times 3$ 矩阵表示。

值得注意的是 w b w_b wb​ 不是相对于移动坐标系的角速度，反之， w b w_b wb​ 是相对于刚体上的固定坐标系 { b } \{b\} {b}的角速度。
最后，对于任意的坐标系 { d } \{d\} {d} 下的角速度，可以得到在另一个坐标系 { c } \{c\} {c}下的表达。如果我们知道 R c d R_{cd} Rcd​，那么有：
w c = R c d w d w_c = R_{cd}w_d wc​=Rcd​wd​

旋转的指数坐标表示

指数坐标以旋转轴（单位向量 w ^ \hat{w} w^）和绕这根轴的角度 $\theta$ 来表达。 向量 w ^ θ ∈ R 3 \hat{w}\theta \in \mathbb{R}^3 w^θ∈R3 作为旋转的三参数指数坐标。而将 w ^ , θ \hat{w}, \theta w^,θ 分开写是轴-角的表示方法。
对于一个旋转矩阵 $R$，与其对应的指数坐标表示 w ^ θ \hat{w}\theta w^θ 等价于：

1. 如果与 { s } \{s\} {s}初始是一致的坐标系绕轴 w ^ \hat{w} w^ 旋转了 $\theta$ 角度，那么此坐标系相对了 { s } \{s\} {s} 的方向可以用$R$ 来表示。
2. 如果与 { s } \{s\} {s}初始是一致的坐标系绕 w ^ θ \hat{w}\theta w^θ 旋转了单位时间（ w ^ θ \hat{w}\theta w^θ由这个时间间隔组成），那么此坐标系相对了 { s } \{s\} {s} 的方向可以用$R$ 来表示。
3. 如果与 { s } \{s\} {s}初始是一致的坐标系绕 w ^ \hat{w} w^ 旋转了 $\theta$ 时间，那么此坐标系相对了 { s } \{s\} {s} 的方向可以用$R$ 来表示。
   最后两种视角要求我们以线性微分方程来考虑指数坐标。

线性微分方程的一些必要结论

从一个简单的标量线性微分方程开始：
(3.39) x ˙ ( t ) = a x ( t ) \dot{x}(t) = ax(t) \tag{3.39} x˙(t)=ax(t)(3.39)
其中，$x(t)\in \mathbb{R},a\in \mathbb{R}$，给定初值为 x ( 0 ) = x 0 x(0) = x_0 x(0)=x0​。
式（3.39）有解：
x ( t ) = e a t x 0 x(t) = e^{at}x_0 x(t)=eatx0​
指数级数展开为：
e a t = 1 + a t + ( a t ) 2 2 ! + ( a t ) 3 3 ! + ⋯   . e^{at} = 1+ at + \frac{(at)^2}{2!} + \frac{(at)^3}{3!} +\cdots. eat=1+at+2!(at)2​+3!(at)3​+⋯.
现在考虑线性微分方程：
(3.40) x ˙ ( t ) = A x ( t ) \dot{x}(t) = Ax(t) \tag{3.40} x˙(t)=Ax(t)(3.40)
其中， x ( t ) ∈ R n , A ∈ n × n x(t)\in\mathbb{R}^n, A\in\mathbb{n \times n} x(t)∈Rn,A∈n×n 是常量，给定初值条件 x ( 0 ) = x 0 x(0)=x_0 x(0)=x0​。由以上的标量结果，我们猜想方程是解为：
(3.41) x ( t ) = e A t x 0 x(t) = e^{At}x_0 \tag{3.41} x(t)=eAtx0​(3.41)
其中，矩阵的级数展开定义为：
(3.42) e A t = I + A t + ( A t ) 2 2 ! + ( A t ) 3 3 ! + ⋯   . e^{At} = I+ At + \frac{(At)^2}{2!} + \frac{(At)^3}{3!} +\cdots. \tag{3.42} eAt=I+At+2!(At)2​+3!(At)3​+⋯.(3.42)
对于任意的方阵， A B = ̸ B A AB =\not BA AB≠​BA，但是对任意的方阵$A$， 任意的标量 $t$，始终有：
(3.44) A e A t = e A t A Ae^{At} = e^{At}A \tag{3.44} AeAt=eAtA(3.44)
所以有：
x ˙ ( t ) = A e A t x 0 = e A t A x 0 \dot{x}(t) = Ae^{At}x_0 = e^{At}Ax_0 x˙(t)=AeAtx0​=eAtAx0​
由于矩阵指数是一种无穷级数，可定义一种闭环表达。如 A = P D P − 1 A = PDP^{-1} A=PDP−1，对于 D ∈ R n × n D\in \mathbb{R}^{n\times n} D∈Rn×n，可逆矩阵 P ∈ R n × n P \in \mathbb{R}^{n \times n} P∈Rn×n，则有：
(3.45) e A t = I + A t + ( A t ) 2 2 ! + ⋯ = I + ( P D P − 1 ) t + ( P D P − 1 ) ( P D P − 1 ) t 2 2 ! + ⋯ = P ( I + D t + ( D t ) 2 2 ! + ⋯   ) P − 1 = P e D t P − 1 \begin{aligned} e^{At} &= I + At + \frac{(At)^2}{2!} + \cdots \\ &= I + (PDP^{-1})t + (PDP^{-1})(PDP^{-1})\frac{t^2}{2!} + \cdots \\ &= P(I +Dt + \frac{(Dt)^2}{2!}+\cdots)P^{-1} \\ &= Pe^{Dt}P^{-1} \end{aligned} \tag{3.45} eAt​=I+At+2!(At)2​+⋯=I+(PDP−1)t+(PDP−1)(PDP−1)2!t2​+⋯=P(I+Dt+2!(Dt)2​+⋯)P−1=PeDtP−1​(3.45)
倘若 $D$ 是对角阵， D = d i a g { d 1 , d 2 , . . . , d n } D = diag\{d_1, d_2, ...,d_n\} D=diag{d1​,d2​,...,dn​}，其矩阵指数为：
(3.46) e D t = [ e d 1 t 0 ⋯ 0 0 e d 2 t ⋯ 0 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ e d n t ] . e^{Dt} = \left[ \begin{matrix} e^{d_1t} & 0 & \cdots & 0 \\ 0 & e^{d_2t} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & e^{d_nt} \end{matrix} \right]. \tag{3.46} eDt=⎣⎢⎢⎢⎡​ed1​t0⋮0​0ed2​t⋮0​⋯⋯⋱⋯​00⋮edn​t​⎦⎥⎥⎥⎤​.(3.46)

定理
线性微分方程 x ( t ) ˙ = A x ( t ) \dot{x(t)} = Ax(t) x(t)˙​=Ax(t)，初值为 x ( 0 ) = x 0 x(0) = x_0 x(0)=x0​，其中 A ∈ R n × n A \in \mathbb{R}^{n \times n} A∈Rn×n 是常量， x ( t ) ∈ R n x(t) \in \mathbb{R}^n x(t)∈Rn，有解：
(3.47) x ( t ) = e A t x 0 x(t) = e^{At}x_0 \tag{3.47} x(t)=eAtx0​(3.47)
其中：
(3.48) e A t = I + t A + t 2 2 ! A 2 + t 3 3 ! A 3 + ⋯   . e^{At} = I + tA + \frac{t^2}{2!}A^2 + \frac{t^3}{3!}A^3 + \cdots. \tag{3.48} eAt=I+tA+2!t2​A2+3!t3​A3+⋯.(3.48)
矩阵 e A t e^{At} eAt 进一步满足以下条件：

1. d ( e A t ) / d t = A e A t = e A t A d(e^{At})/dt = Ae^{At} = e^{At}A d(eAt)/dt=AeAt=eAtA.
2. 如果 A = P D P − 1 A = PDP^{-1} A=PDP−1, 则有 e A t = P e D t P − 1 e^{At} = Pe^{Dt}P^{-1} eAt=PeDtP−1.
3. 如果 $AB=BA$，则有 e A e B = e A + B e^Ae^B = e^{A+B} eAeB=eA+B.
4. ( e A ) − 1 = e − A (e^A)^{-1} = e^{-A} (eA)−1=e−A.

其中，第4个性质可由第三个中令 $B=-A$ 得到。即 e A e − A = I e^{A}e^{-A} = I eAe−A=I，则有第四个性质。

旋转的指数坐标

旋转的指数坐标可以两种视角看待：

1. 绕单位旋转轴 w ^ \hat{w} w^ ( w ^ ∈ R 3 , ∣ ∣ w ^ ∣ ∣ = 1 \hat{w} \in \mathbb{R}^3, ||\hat{w}|| = 1 w^∈R3,∣∣w^∣∣=1)旋转了角度 $\theta \in \mathbb{R}$。
2. 将上述两者相乘，得到三维向量 w ^ θ ∈ R 3 \hat{w}\theta \in \mathbb{R}^3 w^θ∈R3。

当我们表达机器人关节的运动时，第一种更具优势，可以把绕轴旋转的角度分离。

如图3.11所示，三维向量 $p(0)$ 绕着 w ^ \hat{w} w^ 旋转了 $\theta$ 角度，这里我们假设所有的量都是在固定坐标系下的表示。此次旋转过程还可以通过将 $p(0)$ 绕着 w ^ \hat{w} w^ 轴，以恒定速度 $1rad/s$ 从 $t=0$ 到 $t=\theta$ 旋转到达。以 $p(t)$ 来表示向量的路径，则速度 p ˙ ( t ) \dot{p}(t) p˙​(t) 为：
(3.49) p ˙ = w ^ × p \dot{p} = \hat{w} \times p \tag{3.49} p˙​=w^×p(3.49)
证明过程：$p(t)$ 与 w ^ \hat{w} w^ 间的恒定夹角为 $\varphi$，注意到$p$ 的轨迹为一个绕着 w ^ \hat{w} w^ 半径为 $||p||sin\varphi$ 的圆弧。速度 p ˙ \dot{p} p˙​ 与路径相切，由此推导。
同样上式可以表示为：
(3.50) p ˙ = [ w ^ ] p \dot{p} = [\hat{w}]p \tag{3.50} p˙​=[w^]p(3.50)
初值条件为$p(0)$。这是 x ˙ = A x \dot{x} = Ax x˙=Ax 形式的微分方程，解为：
(3.50) p ( t ) = e [ w ^ ] t p ( 0 ) p(t) = e^{[\hat{w}]t}p(0) \tag{3.50} p(t)=e[w^]tp(0)(3.50)
由于$t,\theta$ 是可交换的，等式也可以写为：
p ( θ ) = e [ w ^ ] θ p ( 0 ) p(\theta) = e^{[\hat{w}]\theta}p(0) p(θ)=e[w^]θp(0)
对矩阵指数 e [ w ^ ] θ e^{[\hat{w}]\theta} e[w^]θ 级数展开，直接的有 [ w ^ ] 3 = − [ w ^ ] [\hat{w}]^3 = -[\hat{w}] [w^]3=−[w^]， [ w ^ ] 4 = − [ w ^ ] 2 [\hat{w}]^4 = -[\hat{w}]^2 [w^]4=−[w^]2， [ w ^ ] 5 = [ w ^ ] [\hat{w}]^5 = [\hat{w}] [w^]5=[w^]，则有：
e [ w ^ ] θ = I + [ w ^ ] θ + [ w ^ ] 2 θ 2 2 ! + [ w ^ ] 3 θ 3 3 ! + ⋯ = I + ( θ − θ 3 3 ! + θ 5 5 ! − ⋯   ) [ w ^ ] + ( θ 2 2 ! − θ 4 4 ! + θ 6 6 ! − ⋯   ) [ w ^ ] 2 \begin{aligned} e^{[\hat{w}]\theta} &= I + [\hat{w}]\theta + [\hat{w}]^2\frac{\theta^2}{2!} + [\hat{w}]^3\frac{\theta^3}{3!} + \cdots \\ &= I + (\theta - \frac{\theta^3}{3!} + \frac{\theta^5}{5!} - \cdots)[\hat{w}] + (\frac{\theta^2}{2!} - \frac{\theta^4}{4!} +\frac{\theta^6}{6!} - \cdots)[\hat{w}]^2 \end{aligned} e[w^]θ​=I+[w^]θ+[w^]22!θ2​+[w^]33!θ3​+⋯=I+(θ−3!θ3​+5!θ5​−⋯)[w^]+(2!θ2​−4!θ4​+6!θ6​−⋯)[w^]2​
同时有：
s i n θ = θ − θ 3 3 ! + θ 5 5 ! − ⋯ c o s θ = 1 − θ 2 2 ! − θ 4 4 ! − ⋯ sin\theta = \theta - \frac{\theta^3}{3!} + \frac{\theta^5}{5!} - \cdots \\ cos\theta = 1 - \frac{\theta^2}{2!} - \frac{\theta^4}{4!} - \cdots sinθ=θ−3!θ3​+5!θ5​−⋯cosθ=1−2!θ2​−4!θ4​−⋯

定理
给定一个向量 w ^ θ ∈ R 3 \hat{w}\theta \in \mathbb{R}^3 w^θ∈R3，$\theta$ 为任意标量， w ^ ∈ R 3 \hat{w} \in \mathbb{R}^3 w^∈R3 是单位向量， [ w ^ θ ] [\hat{w}\theta] [w^θ]的矩阵指数为 [ w ^ ] θ = [ w ^ θ ] ∈ s o ( 3 ) [\hat{w}]\theta = [\hat{w}\theta] \in so(3) [w^]θ=[w^θ]∈so(3)：
(3.51) R o t ( w ^ , θ ) = e [ w ^ ] θ = I + s i n θ [ w ^ ] + ( 1 − c o s θ ) [ w ^ ] 2 ∈ S O ( 3 ) Rot(\hat{w},\theta) = e^{[\hat{w}]\theta} = I + sin\theta[\hat{w}] + (1-cos\theta)[\hat{w}]^2 \in SO(3) \tag{3.51} Rot(w^,θ)=e[w^]θ=I+sinθ[w^]+(1−cosθ)[w^]2∈SO(3)(3.51)
上式也即罗德里格斯旋转公式。
可以看到，使用矩阵指数来创造一个绕轴 w ^ \hat{w} w^旋转的矩阵。进一步的， e [ w ^ ] θ p e^{[\hat{w}]\theta}p e[w^]θp 具有把 p ∈ R 3 p \in \mathbb{R}^3 p∈R3 绕着固定轴 w ^ \hat{w} w^ 旋转$\theta$ 角度的效果。

类似的，考虑由三个列向量组成的旋转矩阵$R$，旋转矩阵 R ′ = e [ w ^ ] θ R = R o t ( w ^ , θ ) R R' = e^{[\hat{w}]\theta}R = Rot(\hat{w}, \theta)R R′=e[w^]θR=Rot(w^,θ)R，是将$R$ 绕着固定坐标系里的 w ^ \hat{w} w^ 旋转$\theta$ 角后的方向。而 R ′ ′ = R e [ w ^ ] θ = R R o t ( w ^ , θ ) R'' = Re^{[\hat{w}]\theta} = RRot(\hat{w}, \theta) R′′=Re[w^]θ=RRot(w^,θ)，是将$R$ 在刚体坐标系里的 w ^ \hat{w} w^ 旋转$\theta$ 角后的方向。

下一步的任务是证明对于任意的 $R\in SO(3)$，总是能找到一个单位向量 w ^ \hat{w} w^ 和一个标量 $\theta$，使得 R = e [ w ^ ] θ R = e^{[\hat{w}]\theta} R=e[w^]θ。

旋转的矩阵对数

如果 w ^ θ \hat{w}\theta w^θ 表示旋转矩阵 $R$ 的指数坐标，那么反对称阵 [ w ^ θ ] = [ w ^ ] θ [\hat{w}\theta] = [\hat{w}]\theta [w^θ]=[w^]θ 是旋转矩阵的矩阵对数。正如矩阵指数给出了以角速度 [ w ^ ] θ [\hat{w}]\theta [w^]θ 旋转一秒的旋转矩阵$R\in SO(3)$，矩阵对数用来寻找恒定的角速度 [ w ^ ] θ ∈ s o ( 3 ) [\hat{w}]\theta \in so(3) [w^]θ∈so(3)，在这样的角速度下，旋转一秒使 $I$ 转到 $R$。或者说：
e x p : [ w ^ ] θ ∈ s o ( 3 ) → R ∈ S O ( 3 ) l o g : R ∈ S O ( 3 ) → [ w ^ ] θ ∈ s o ( 3 ) exp: [\hat{w}]\theta \in so(3) \to R \in SO(3) \\ log: R \in SO(3) \to [\hat{w}]\theta \in so(3) exp:[w^]θ∈so(3)→R∈SO(3)log:R∈SO(3)→[w^]θ∈so(3)
将 e [ w ^ ] θ e^{[\hat{w}]\theta} e[w^]θ展开得到：
[ c θ + w 1 ^ 2 ( 1 − c θ ) w 1 ^ w 2 ^ ( 1 − c θ ) − w 3 ^ s θ w 1 ^ w 3 ^ ( 1 − c θ ) + w 2 ^ s θ w 1 ^ w 2 ^ ( 1 − c θ ) + w 3 ^ s θ c θ + w 2 ^ 2 ( 1 − c θ ) w 2 ^ w 3 ^ ( 1 − c θ ) − w 1 ^ s θ w 1 ^ w 3 ^ ( 1 − c θ ) − w 2 ^ s θ w 2 ^ w 3 ^ ( 1 − c θ ) + w 1 ^ s θ c θ + w 3 ^ 2 ( 1 − c θ ) ] \left[ \begin{matrix} c_\theta+\hat{w_1}^2(1-c_\theta) & \hat{w_1}\hat{w_2}(1-c_\theta) - \hat{w_3}s_\theta & \hat{w_1}\hat{w_3}(1-c_\theta) + \hat{w_2}s_\theta \\ \hat{w_1}\hat{w_2}(1-c_\theta) + \hat{w_3}s_\theta & c_\theta+\hat{w_2}^2(1-c_\theta) & \hat{w_2}\hat{w_3}(1-c_\theta) - \hat{w_1}s_\theta \\ \hat{w_1}\hat{w_3}(1-c_\theta) - \hat{w_2}s_\theta & \hat{w_2}\hat{w_3}(1-c_\theta) + \hat{w_1}s_\theta & c_\theta+\hat{w_3}^2(1-c_\theta) \end{matrix} \right] ⎣⎡​cθ​+w1​^​2(1−cθ​)w1​^​w2​^​(1−cθ​)+w3​^​sθ​w1​^​w3​^​(1−cθ​)−w2​^​sθ​​w1​^​w2​^​(1−cθ​)−w3​^​sθ​cθ​+w2​^​2(1−cθ​)w2​^​w3​^​(1−cθ​)+w1​^​sθ​​w1​^​w3​^​(1−cθ​)+w2​^​sθ​w2​^​w3​^​(1−cθ​)−w1​^​sθ​cθ​+w3​^​2(1−cθ​)​⎦⎤​

其中， w ^ = ( w ^ 1 , w ^ 2 , w ^ 3 ) \hat{w} = (\hat{w}_1, \hat{w}_2,\hat{w}_3) w^=(w^1​,w^2​,w^3​)，让上述矩阵等于$R\in SO(3)$，有：
r 32 − r 23 = 2 w ^ 1 s i n θ r 13 − r 31 = 2 w ^ 2 s i n θ r 21 − r 12 = 2 w ^ 3 s i n θ r_{32} - r_{23} = 2\hat{w}_1sin\theta \\ r_{13} - r_{31} = 2\hat{w}_2sin\theta \\ r_{21} - r_{12} = 2\hat{w}_3sin\theta r32​−r23​=2w^1​sinθr13​−r31​=2w^2​sinθr21​−r12​=2w^3​sinθ
只要 s i n θ = ̸ 0 sin \theta =\not 0 sinθ≠​0（或者说$\theta$不是$\pi$的整数倍），可以得到：
w ^ 1 = 1 2 s i n θ ( r 32 − r 23 ) w ^ 2 = 1 2 s i n θ ( r 13 − r 31 ) w ^ 3 = 1 2 s i n θ ( r 21 − r 12 ) \hat{w}_1 = \frac{1}{2sin\theta}(r_{32} - r_{23}) \\ \hat{w}_2 = \frac{1}{2sin\theta}(r_{13} - r_{31}) \\ \hat{w}_3 = \frac{1}{2sin\theta}(r_{21} - r_{12}) w^1​=2sinθ1​(r32​−r23​)w^2​=2sinθ1​(r13​−r31​)w^3​=2sinθ1​(r21​−r12​)
也可以用反对称阵表达为：
(3.53) [ w ^ ] = [ 0 − w ^ 3 w ^ 2 w ^ 3 0 − w ^ 1 − w ^ 2 w ^ 1 0 ] = 1 2 s i n θ ( R − R T ) [\hat{w}] = \left[ \begin{matrix} 0 & -\hat{w}_3 & \hat{w}_2 \\ \hat{w}_3 & 0 & -\hat{w}_1 \\ -\hat{w}_2 & \hat{w}_1 & 0 \end{matrix} \right] = \frac{1}{2sin\theta}(R - R^T) \tag{3.53} [w^]=⎣⎡​0w^3​−w^2​​−w^3​0w^1​​w^2​−w^1​0​⎦⎤​=2sinθ1​(R−RT)(3.53)

回忆下， w ^ \hat{w} w^ 表示的是给定旋转矩阵 $R$ 的旋转轴。由于$sin\theta$ 在分母上，如果 $\theta$ 是 $\pi$ 的整数倍时， [ w ^ ] [\hat{w}] [w^] 便不好定义，这个情况后面再说。先假设 s i n θ = ̸ 0 sin\theta =\not0 sinθ≠​0，然后找到$\theta$ 的表达式。取式(3.52)矩阵的迹trace，且有 w ^ 1 2 + w ^ 2 2 + w ^ 3 2 = 1 \hat{w}_1^2 + \hat{w}_2^2 + \hat{w}_3^2 = 1 w^12​+w^22​+w^32​=1：
(3.54) t r R = r 11 + r 22 + r 33 = 1 + 2 c o s θ tr R = r_{11} + r_{22} + r_{33} = 1+2cos\theta \tag{3.54} trR=r11​+r22​+r33​=1+2cosθ(3.54)
对于满足$1+2cos\theta =trR$ 的，且不是$\pi$的整数倍的$\theta$， [ w ^ ] [\hat{w}] [w^] 矩阵可以由式（3.53）表示。
而对于$\theta =k\pi$ 的情况，先不要管 w ^ \hat{w} w^，我们先使 $R=I$，那么 w ^ \hat{w} w^ 就没有定义。当$k$ 是奇数时，由式（3.51)，有：
(3.55) R = e [ w ^ ] π = I + 2 [ w ^ ] 2 R = e^{[\hat{w}]\pi} = I +2[\hat{w}]^2 \tag{3.55} R=e[w^]π=I+2[w^]2(3.55)
对角线上的元素为：
(3.56) w ^ i = ± r i i + 1 2 , i = 1 , 2 , 3 \hat{w}_i = \pm\sqrt{\frac{r_{ii}+1}{2}}, i=1,2,3 \tag{3.56} w^i​=±2rii​+1​ ​,i=1,2,3(3.56)
非对角元素有如下等式：
(3.57) 2 w ^ 1 w ^ 2 = r 12 , 2 w ^ 2 w ^ 3 = r 23 , 2 w ^ 1 w ^ 3 = r 13 , 2\hat{w}_1\hat{w}_2 = r_{12},\\ 2\hat{w}_2\hat{w}_3 = r_{23},\\ \tag{3.57} 2\hat{w}_1\hat{w}_3 = r_{13}, 2w^1​w^2​=r12​,2w^2​w^3​=r23​,2w^1​w^3​=r13​,(3.57)
从等式（3.55）我们知道$R$必须是对称阵： r 12 = r 21 r_{12} = r_{21} r12​=r21​， r 23 = r 32 r_{23} = r_{32} r23​=r32​， r 13 = r 31 r_{13} = r_{31} r13​=r31​。式（3.56）和式（3.57）可能都需要来求取 w ^ \hat{w} w^。一旦找到解，则 R = e [ w ^ ] θ R = e^{[\hat{w}]\theta} R=e[w^]θ，其中 $\theta =\pm \pi ,\pm 3\pi ，\cdots$
我们把$\theta$ 的取值限制在$[0，\pi ]$，那么下面的算法可用于旋转矩阵的对数。

算法
给定一个$R\in SO(3)$，找到一个$\theta \in [0,\pi ]$ 和一个单位旋转轴 w ^ ∈ R 3 \hat{w} \in \mathbb{R}^3 w^∈R3, ∣ ∣ w ^ ∣ ∣ = 1 ||\hat{w}|| = 1 ∣∣w^∣∣=1 ，那么 e [ w ^ ] θ = R e^{[\hat{w}]\theta} = R e[w^]θ=R。反对称阵 [ w ^ ] θ ∈ s o ( 3 ) [\hat{w}]\theta \in so(3) [w^]θ∈so(3) 是矩阵的对数。

1. 如果 $R=I$， 那么 $\theta =0$， w ^ \hat{w} w^ 无定义。

2. 如果 $trR=-1$，那么 $\theta =\pi$。 w ^ \hat{w} w^ 取下列三个值的任一个均可：
   (3.58) w ^ = 1 2 ( 1 + r 33 ) [ r 13 r 23 1 + r 33 ] \hat{w} = \frac{1}{\sqrt{2(1+r_{33})}} \left[ \begin{matrix} r_{13} \\ r_{23} \\ 1+r_{33} \end{matrix} \right] \tag{3.58} w^=2(1+r33​) ​1​⎣⎡​r13​r23​1+r33​​⎦⎤​(3.58)
   或：
   (3.59) w ^ = 1 2 ( 1 + r 22 ) [ r 12 1 + r 22 r 32 ] \hat{w} = \frac{1}{\sqrt{2(1+r_{22})}} \left[ \begin{matrix} r_{12} \\ 1+r_{22} \\ r_{32} \end{matrix} \right] \tag{3.59} w^=2(1+r22​) ​1​⎣⎡​r12​1+r22​r32​​⎦⎤​(3.59)
   或：
   (3.60) w ^ = 1 2 ( 1 + r 11 ) [ 1 + r 11 r 21 r 31 ] \hat{w} = \frac{1}{\sqrt{2(1+r_{11})}} \left[ \begin{matrix} 1+r_{11} \\ r_{21} \\ r_{31} \end{matrix} \right] \tag{3.60} w^=2(1+r11​) ​1​⎣⎡​1+r11​r21​r31​​⎦⎤​(3.60)

3. 否则 θ = c o s − 1 ( 1 2 ( t r R − 1 ) ) ∈ [ 0 , π ) \theta = cos^{-1}(\frac{1}{2}(tr R-1))\in[0, \pi) θ=cos−1(21​(trR−1))∈[0,π)，且：
   (3.61) [ w ^ ] = 1 2 s i n θ ( R − R T ) [\hat{w}] = \frac{1}{2sin\theta}(R-R^T) \tag{3.61} [w^]=2sinθ1​(R−RT)(3.61)
   由于每个$R\in SO(3)$ 满足上述三个条件中的一个，所以对于每一个 $R$ 都存在一个矩阵对数 [ w ^ ] θ [\hat{w}]\theta [w^]θ，即指数坐标 w ^ θ \hat{w}\theta w^θ。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！