利用梯度算法,求解线性模型(y=wx+b)的最优参数w,b
一、损失函数
![]()
代码实现:
# y = wx + b 接收参数b,w和点(x,y)def compute_error_for_line_given_points(b, w, points):totalError = 0for i in range(0, len(points)):x = points[i, 0]y = points[i, 1]totalError += (y - (w * x + b)) ** 2return totalError / float(len(points))二、梯度下降算法

以上图为例:在该点的梯度为:![]()
![]()
导数大于0,说明是在上升,小于0是在下降。
所以在如上该点处,如果要往回走,就需取得导数的负方向。
所以 w=w-a![]()
三、利用梯度下降求使损失函数最小的 w和b值
![]()
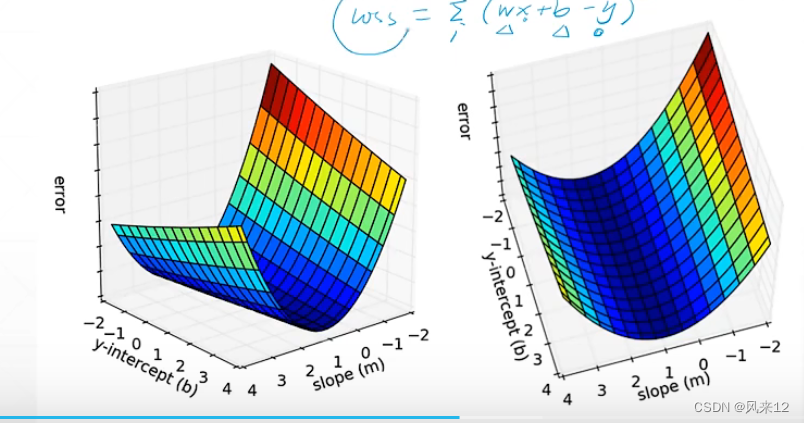
自变量为w和b。
![]() 分别计算loss 对w和b的偏微分。
分别计算loss 对w和b的偏微分。
![]() =2(wx+b-y)x
=2(wx+b-y)x
![]()
得到了一个所有点下面的avg梯度信息以后,用这个梯度信息*学习率。
def step_gradient(b_current, w_current, points, learningRate):b_gradient = 0w_gradient = 0N = float(len(points))for i in range(0, len(points)):x = points[i, 0]y = points[i, 1]b_gradient += -(2/N) * (y - ((w_current * x) + b_current))w_gradient += -(2/N) * x * (y - ((w_current * x) + b_current))new_b = b_current - (learningRate * b_gradient)new_m = w_current - (learningRate * w_gradient)return [new_b, new_m]循环迭代梯度信息

四、第二种代码实现方式
x_data=[1.0,2.0,3.0]
y_data=[2.0,4.0,6.0]w=1.0def forward(x):return x*w#zip() 函数将对象中对应的元素打包成一个个元组,然后返回由这些元组组成的列表。
def cost(xs,ys):cost=0for x,y in zip(xs,ys):y_pred=forward(x)cost+=(y_pred-y)**2return cost/len(xs)def gradient(xs,ys):grad=0for x,y in zip(xs,ys):grad+=2*x*(x*w-y)return grad/len(xs)print("Predict (befor traing)",4,forward(4))
#range(100)指的是默认从0开始,步长为1,不包括100
for epoch in range(100):cost_val=cost(x_data,y_data)grad_val=gradient(x_data,y_data)w-=0.01*grad_valprint('Epoch:',epoch,'w=',w,'loss=',cost_val)print('Predict(after training',4,forward(4))输出结果: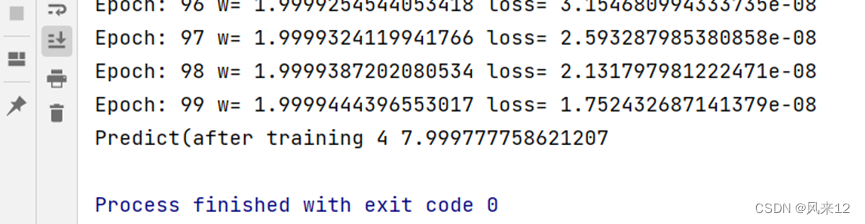
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!