遥感物理基础

绪论

• 广义遥感：泛指一切非接触的远距离感知/探测，通过对收集/感知的信息 (重力、磁力、声波、地震波、电磁波)，进行分析、处理，在不与物体物理接触情况下识别目标(位置、属性、分布、运动规律等)的一种探测方式。

• 遥感图像的像素值：某一时刻 t，在不同波长 \lambda 和不同极化（偏振）方向 p 上所收集到的位于坐标 (x,y) 的目标物的电磁波辐射能量：图像能量 = 目标反射+目标发散

  $$L(x,y,t,\lambda,p)=[1-\beta(x,y,t,\lambda,p)]\cdot E(\lambda)+\beta(x,y,t,\lambda,p)\cdot I(x,y,t,\lambda)$$

   

  其中\beta为反射率，t为摄像时间，p为极化偏振方向

一、地物的反射特性

1.1 电磁波及其性质

• 电磁波谱：电磁波依据波长大小依次排练

• 大气窗口：大气通过率较高的谱段

• 基于电磁波谱的遥感分类：

  • 紫外 0.05-0.38

  • 可见光 0.4-0.76

  • 红外 0.76-1000

    • 近红外NIR：0.76-1.35

    • 短波红外SWIR：1.35-3

    • 中红外MIR：3-8

    • 热红外TIR：8-15

    • 远红外RFIR：15-1000

  • 微波：1mm-1000m

• 电磁波的来源：任何高于绝对零度的物质都会向外界辐射电磁波，其波长与物体内部活动有关

• 太阳光谱

  • 太阳常数：指不受大气影响，在距离太阳一个天文单位内 (日地平均距离处)，垂直于太阳光辐射的方向上，单位面积单位时间黑体所接收的太阳辐射能量：I_{0}\approx 1360\text{W}/m^{2}

• 地球光谱

  • 在中红外部分，遥感信号既有太阳反射部分也有地球发射部分

  • 在中红外部分观测地表温度需要去除太阳反射部分的能量

1.2 表征电磁波的物理量及转换

详细参考辐射基础系列

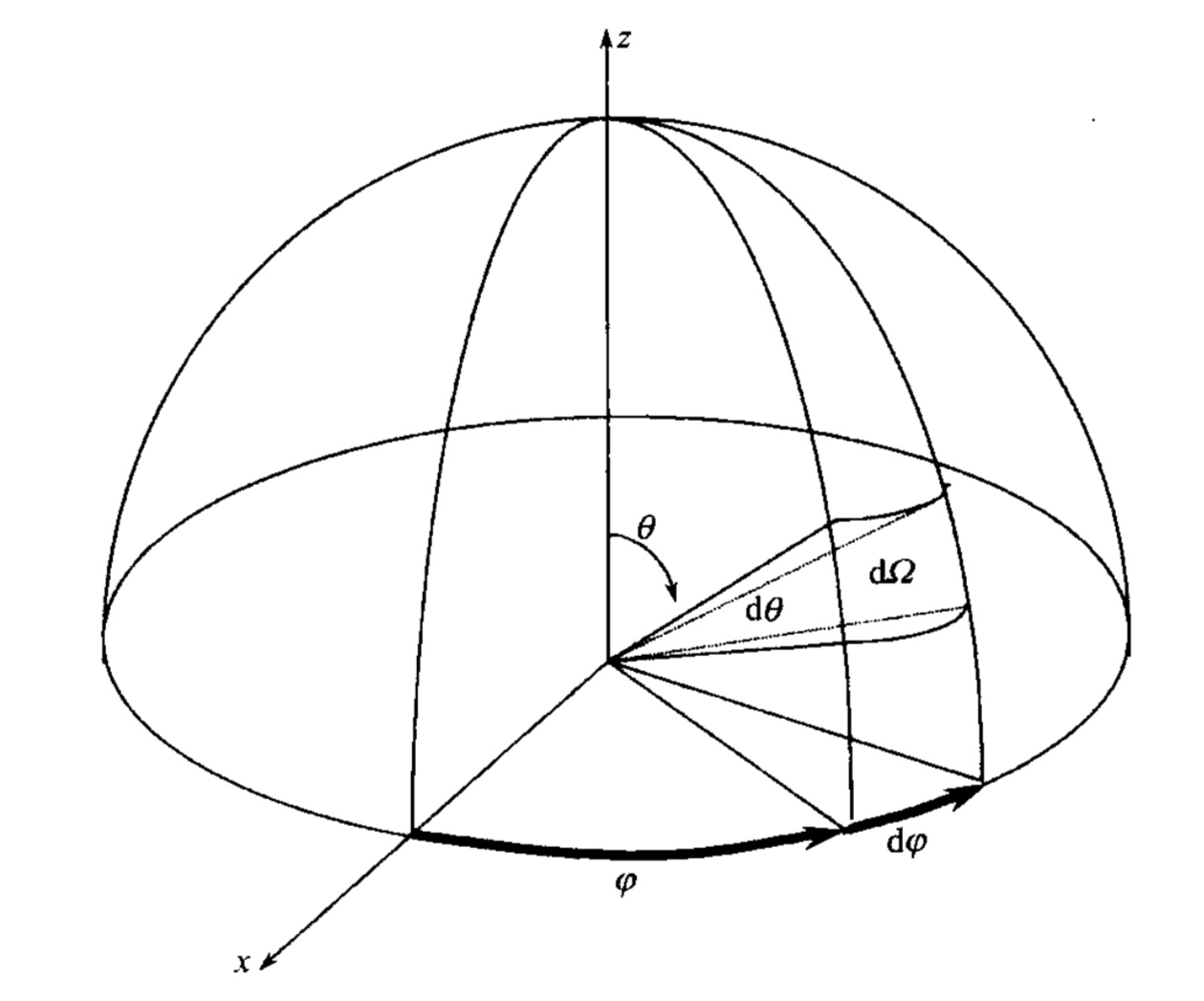
• 立体角：球面上单位面积对球心的张角，即球半径为 r 的球面被一个圆锥所裁取的球面表面积与球半径的平方的比 \Omega=\frac{\text{A}}{r^{2}} 其中 A 为单位面积，单位：球面度 Sr

  $$
  \text{d}A=(r \text{d}\theta)(r \sin \theta\text{d}\varphi)=r^{2}\sin \theta \text{d}\theta\text{d}\varphi \\ \text{d}\Omega=\frac{\text{d}\text{A}}{r^{2}}=\sin \theta \text{d}\theta\text{d}\varphi
  $$

• 

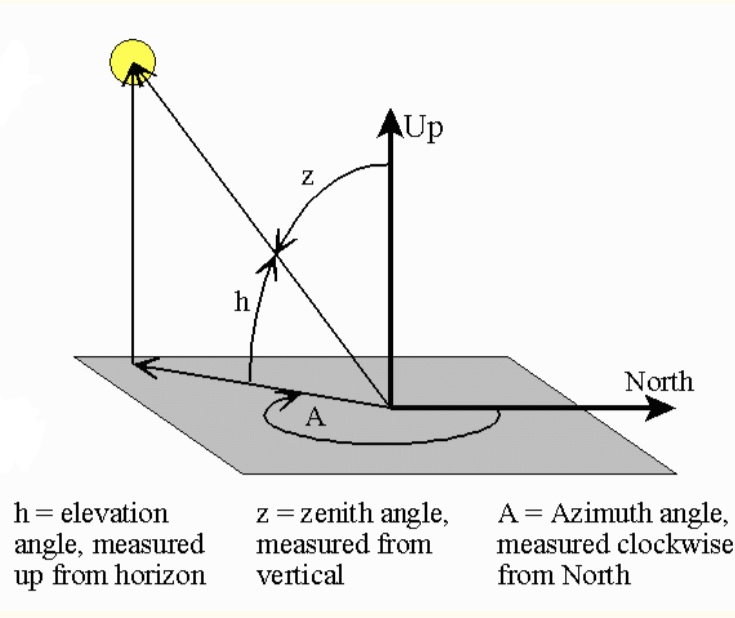
• 天顶角 \theta（Zenith Angle ）：入射/观测方向与当地天顶方向的夹角

  • 范围： \left( 0,\frac{\pi}{2} \right)

• 高度角：天顶角的补角

• 方位角 \varphi（Azimuth）：参考方向(正北方) 与入射/观测方向的夹角

  • 范围： (0,2\pi)

    

• 辐射能量 Q\,\,(\text{J})：电磁场所具有的能量，电磁波波长越短，能量越大

• 辐射通量 \Phi：单位时间内，通过某一面积的辐射能量，也称辐射功率

  $$
  \Phi = \frac{\text{d}Q}{\text{d}t}
  $$

   

  单位：\text{W=J/s}

• 辐射强度 I：点辐射源在某一方向上单位立体角内的辐射通量

  • 描述点辐射源强度的物理量

    $$
    I = \frac{\text{d}\Phi}{\text{d}\Omega}
    $$

     

    单位：\text{W}/Sr

  • 如果是各向同辐射源，则 I=\frac{E}{4\pi}

• 辐射出射度 M ：面辐射元 单位面积向半球空间发射的辐射通量

  • $$
    M = \frac{\text{d}\Phi}{\text{d}A}
    $$

     

    单位：\text{W}/m^{2}

• 辐照度 E ：单位时间内，接收到的辐射通量

  $$
  E = \frac{\text{d}\Phi}{\text{d}A}
  $$

   

  单位：\text{W}/m^{2}，\text{W}/(m^{2}\cdot \mu m)

• 距离平方反比定律：某点的辐照度和其距离发光点的距离的平方呈反比关系。

  • 推导：

    $$
    E = \frac{\text{d}\Phi}{\text{d}A}=\frac{\text{d}\Phi}{\text{d}\Omega}\cdot \frac{\text{d}\Omega}{\text{d}A}=I\cos\theta\cdot r^2
    $$

  • 尽管点源的辐射强度不变，点源对被照物所张的立体角随距离增加而减小

  • 平面辐照度与辐射强度的余弦关系

• 辐射亮度 L：单位投影面积上单位立体角内的辐射通量

  $$
  L=\frac{\text{d}^2\Phi}{\text{d}\Omega\text{d}A\cos \theta}\\L=\frac{\text{d}}{\text{d}A}\left( \frac{\text{d} \Phi}{\text{d}\Omega} \right)\cdot \frac{1}{\cos \theta}= \frac{\text{d}I}{\text{d}A \cos \theta}\\L=\frac{\text{d}}{\text{d}\Omega}\left( \frac{\text{d} \Phi}{\text{d}A} \right)\cdot \frac{1}{\cos \theta}= \frac{\text{d}M}{\text{d}\Omega \cos \theta}=\frac{\text{d}E}{\text{d}\Omega \cos \theta}
  $$

   

  单位：W/(Sr\cdot m^2)，光谱辐射亮度单位： W\cdot cm^{-2}\cdot Sr^{-1}\cdot \mu m^{-1}

  • 指单位立体角，单位面积上和在单位波长上的通量

  • 用来描述面光源强弱的物理量

  • 遥感观测信号即为辐射亮度

  • 式2为辐射源的面远很小看作点光源

  • 特点：沿辐射方向辐射亮度不变，与距离无关

• 朗伯体：对某些自身发射(或反射) 辐射的物体，其辐射亮度与方向无关，即各个方向的辐射亮度不变

• 朗伯余弦定律：理想情况下，朗伯体单位面积向空间规定方向单位立体角发射(或反射)的辐射强度与该方向与表面法线方向的夹角余弦成正比 I_{\theta}=I_{0}\cos (\theta)

• 朗伯体辐照出射度 M 与辐射亮度 L 的关系： M=\pi L

  • 推导：

  • $$
    L=\frac{\text{d}^{2}\Phi}{\text{d}\Omega\text{d}A\cos \theta}\\L=\frac{\text{d}}{\text{d}\Omega}\left( \frac{\text{d}\Phi}{\text{d}A} \right)\cdot \frac{1}{\cos \theta}\\M=\int\limits_{2\pi}L\cos\theta \,\text{d}\Omega=\int_{0}^{2\pi}\int_{0}^{\frac{\pi}{2}}L\sin\theta\cos\theta \,\text{d}\theta \text{d}\varphi=\pi L
    $$

     

• 口径：传感器光强检测器件的有效几何尺寸

• 视场角：传感器的视场面积（像元）对传感器张的立体角

• 光谱辐射量：在单位波长间隔内的辐射量

• 传感器信号强度与传感器本身的口径、视场角有关，与距离无关

1.3 反射、散射及地物反射光谱特性

• 电磁波在介质中传播：

  • 折射：速度减慢

  • 消光：

    • 散射：光改变其传播方向，从侧面也能看到光

      • 反射（传感器接收）

      • 透射

    • 吸收

• 在热红外和微波区域，还存在介质自身发射的电磁波，增强电磁波强度。

• 能量守恒定律：

  $$
  \Phi_{0}=\Phi_{\rho}+\Phi_{\alpha}+\Phi_{\tau}
  $$

   

  \Phi_{0} 为总能量，\Phi_{\rho} 为反射能量，\Phi_{\alpha} 为吸收能量，\Phi_{\tau} 为透射能量

  $$
  1=\rho + \alpha+ \tau
  $$

   

  \rho 为反射率，\alpha 为吸收率，\tau 为透射率

• 地物反射光谱特性：由于物体自身成分、结构和空间分布不同，对于不同波长的电磁波有选择性的反射，物体反射率随波长而改变的特性

• 粗糙度： \Delta h 为平均粗糙高度

  • 光滑表面 \frac{\Delta h\cos\theta}{8}<\lambda

  • 粗糙表面 \frac{\Delta h\cos\theta}{8}\gg\lambda

• 镜面反射：反射能量集中在一个方向，反射角=入射角

  • 光滑表面

• 漫反射：整个表面都均匀地向各向反射入射光称为漫反射

  • 粗糙表面

• 方向反射：介于漫反射和镜面反射之间，各向都有反射，但各向反射强度不均一。

• 地物波谱特征：该地物对太阳辐射的反射能力随波长而变的规律

• 地物方向谱特征：描述地物对太阳辐射反射能力在方向空间变化

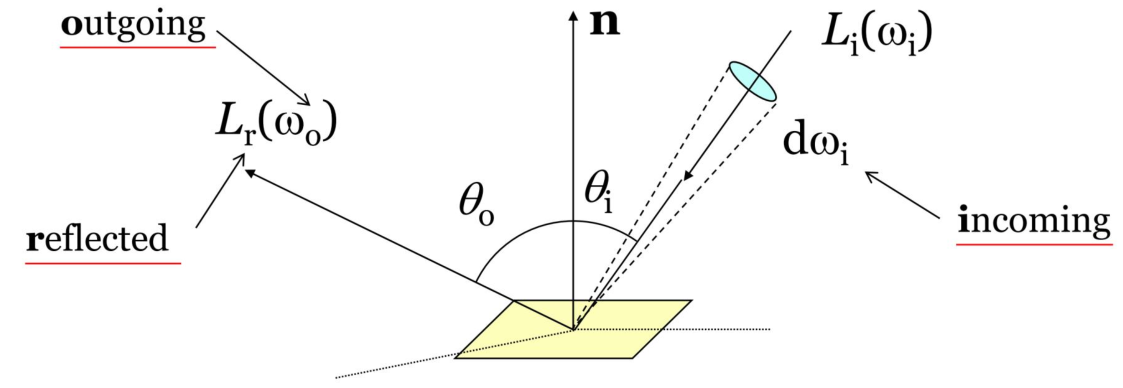
BRDF 双向反射率分布函数(i入射，r反射)

• 给定入射角度，用来描述在某个反射方向上有多少光被反射；是波长、入射角度、观测角度的函数，与地物成分、光学性质、3D 结构、阴影遮挡等密切相关

$$
BRDF(\Omega_i,\Omega_r) = \frac{\text{d}L(\Omega_r)}{\text{d}E(\Omega_i)}\\ f_{r}(\omega_{i}\rightarrow\omega_{0})=\frac{\text{d}L_{r}(\omega_{0})}{L_{i}(\omega_{i})\cdot\cos(\theta_{i})\cdot \text{d}\omega_{i}}[sr^{-1}]
$$

• 对于理想漫反射体：

  $$
  f_P = \frac{\text{d}L_P}{\text{d}E_P}=\frac{\text{d}M_P/\pi}{\text{d}E_P}=\frac{1}{\pi}
  $$

• BRDF的野外测量

  • 顺序测量

  • 同步测量：两台仪器都需要经过绝对辐射定标

BRF 二向性反射率因子

• 在相同的辐照度条件(E_T=E_P)下，地物（T）向 (\theta,\varphi) 方向的反射辐射亮度与一个理想的漫反射体（P）在该方向上的反射辐射亮度之比值

$$
R(\theta_{i},\varphi_{i},\theta_{r},\varphi_{r},\lambda)=\frac{\text{d}L_{T}(\theta_r,\varphi_r,\lambda)}{\text{d}L_{P}(\theta_r,\varphi_r,\lambda)}
$$

• 不仅取决于目标物的非朗伯体特性，而且还与辐射环境有关

• BRDF和BRF的关系：

  $$
  R_T=\frac{\text{d}L_T}{\text{d}L_P}=\frac{\text{d}L_T}{\text{d}E_P/\pi}=\pi\cdot \frac{\text{d}L_T}{\text{d}E_T}=\pi\cdot f_T
  $$

• $$
  R(\theta_{i},\varphi_{i},\theta_{r},\varphi_{r},\lambda)=\frac{L_T(\theta_r,\varphi_r,\lambda)}{\mu_0E_0(\lambda)/\pi}
  $$

   

  其中E_0(\lambda)为垂直入射方向上的太阳辐照度，\mu_0为太阳天顶角的余弦

二向反射率(BRF的一种形式)

• 描述的是目标物在给定方向上的反射率

$$
\rho(\theta_{i},\varphi_{i},\theta_{r},\varphi_{r},\lambda)=\frac{\pi \text{d}L(\theta_{r},\varphi_{r},\lambda)}{\text{d}E(\theta_{i},\varphi_{i},\lambda)}
$$

半球反射率（反照率）

• 目标物的出射度与辐照度之比值

• 描述的是目标物在所有方向上的反射率

  $$
  \rho(\lambda)=\frac{M(\lambda)}{E(\lambda)}
  $$

方向半球反射率（黑天空反射率）

• BRDF 对反射半球角度积分

  $$
  DHR =\int_{-\pi}^{\pi}\int_{0}^{\frac{\pi}{2}}f(\theta_i,\varphi_i;\theta_r,\varphi_r)\cos\theta_{r}\sin\theta_{r}\,\text{d}\theta_{r}\text{d}\varphi_{r}
  $$

双半球反射率（白天空反射率）

• BRDF在入射半球和出射半球空间的积分，也等于DHR在入射半球空间的积分

  $$
  BHR =\frac{\text{d}\Phi(\theta_{i},\varphi_{i},2\pi;2\pi)}{\text{d}\Phi_{i}(\theta_{i},\varphi_{i},2\pi)}=\frac{\text{d} A\int_{2\pi}\text{d} L(\theta_{i},\varphi_{i},2\pi;\theta_{r},\varphi_{r})\cos\theta_{r}\text{d}\Omega_{r}}{d A\int_{2\pi}\text{d} L(\theta_{i},\varphi_{i})\cos\theta_{i}\text{d}\Omega_{i}}
  $$

1.4 光谱响应函数

• 遥感器的固有参数

• 表征了遥感器的某一波段对各个精细的电磁波谱的感应程度

• $$
  \lambda_{等效中心波长}=\frac{\int_{0}^{\infty}\lambda\Gamma(\lambda)\text{d}\lambda}{\int_{0}^{\infty}\Gamma(\lambda)\text{d}\lambda}
  $$

   

二、大气校正

2.1 辐射定标

• 将接收的遥感数据，通常是灰度值（DN），转换成实际的物理量（辐射亮度、反射率等）的过程

• 辐射定标是实现定量化遥感产品反演的前提和基础

• 类型：

  • 发射前/实验室定标

  • 机（星）上定标

  • 地面/定标场定标

    • 绝对辐射定标

    • 场区近似朗伯表面，具有较好的光谱均一性

  • 交叉定标

• L = gain \times DN+offet

  • 增益和偏移的具体数值通常可以从头文件获取

2.2 大气校正

2.2.1 大气对电磁波的作用

• 大气对电磁波的吸收

  • 平流层的臭氧吸收了大约 99%的有害的紫外辐射

  • 水汽吸收几乎覆盖了红外辐射的整个波段

• 大气散射

  • 瑞利散射：粒子大小 D\ll\lambda，通常为大气分子散射，散射强度与波长的四次方成反比

  • 米氏散射：粒子大小D 与入射波长 λ相近,其散 射的光强在各方向是不对称的,通常为气溶胶散射,特点是前向大于后向, 而且随着D/ λ的增大，前向散射比例加大

  • 无选择性散射：粒子大小 D\gg\lambda，散射各向同性，与波长无关

• 黑体：吸收率 = 发射率 = 1

2.2.2 大气校正原理

• 大气校正的过程就是去除遥感信号里面大气对卫星信号的影响（吸收、散射），还原地表真实辐射状况的过程，最终目的得到地表的反射率或离地辐射

• 地表朗伯反射，不考虑地表和大气的多次散射，传感器接收的辐射亮度表示为：

  $$
  L(\mu_0,\mu,\phi,\lambda)=L_0+\mu E_0\gamma^{\downarrow }\gamma^\uparrow\rho/\pi
  $$

   

  L_0：大气程辐射，地表反射率为零时的辐射

  \gamma^\downarrow：入射方向，TOA到地表的总透过率

  \gamma^\uparrow：传感器方向，地表到TOA的总透过率

  \rho：地表反射率

  E_0：TOA太阳辐照度

  \mu：太阳天顶角余弦

• 地表和大气间向上的多次散射：

  $$
  \mu E_0\gamma^\downarrow\rho\times(1+\rho r+\rho^2r^2+\rho^3r^3+...)=\frac{\mu E_0\gamma^\downarrow\rho}{1-\rho r}
  $$

   

  考虑多次散射的传感器接收的辐射还要乘\gamma^\uparrow

2.2.3 大气校正方法

• 辐射传输公式：

  $$
  L=L_0+\frac{f}{1-\pi fr}\mu E_0\gamma^\downarrow\gamma^\uparrow
  $$

• 

• 暗目标法

  • 假设图像存在反射率特别低的地物（水体、阴影、浓密植被），这些区域反射率很低，接近0，然后图像上该区域的辐射值不为0，因此，认为这些区域的辐射值是由于大气影响造成的

  • 校正方法：每个波段的图像整体减去最小值

  • 不足：这种方法仅近似校正了大气程辐射；整幅图像大气影响认为一致；实际暗目标的反射不一定等于0；

  • 该方法可以估算气溶胶光学厚度和像元反射率

• 不变目标法

  • 假设图像存在一些目标（像元），其反射率几乎不随时间变化，利用这些不变目标的反射率，可以建立其他时间的图像（img_1）与参考图像(img_0)的对应数学关系，实现校正其他时间图像(img_1)的目的

三、植被遥感模型

3.1 叶片光谱特征

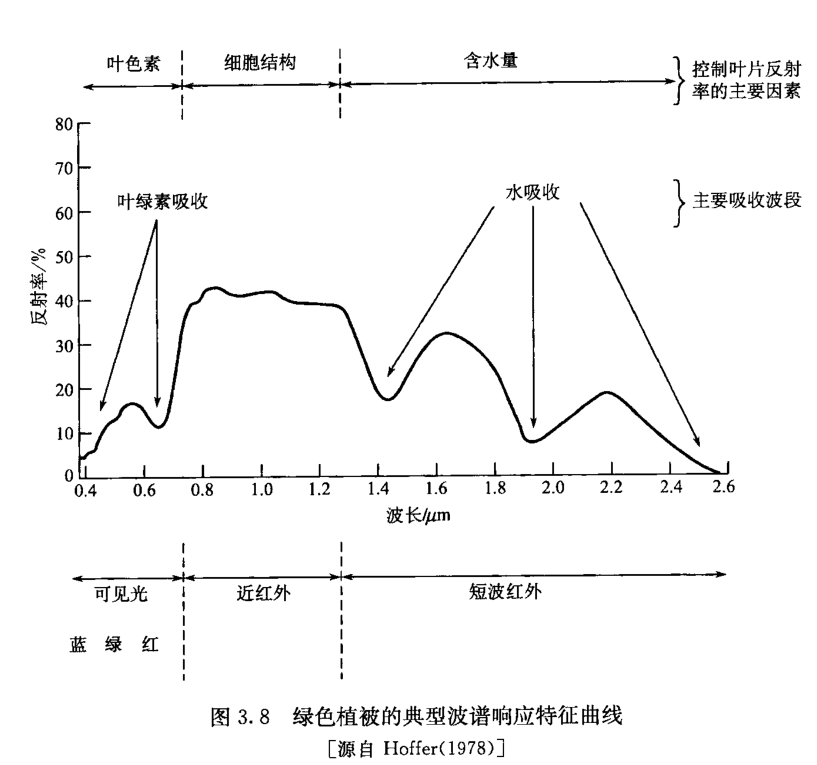
3.1.2 单叶光谱特征

• 0.4-0.7um：0.55um反射峰，0.45和0.65um两个吸收谷

• 0.7-1.2um

• 1.2-2.6um：1.42和1.96两个水分吸收谷

• 红边：反射光谱一阶导数最大值所对应的波长位置，对应红光区外叶绿素吸收减少部位到近红外高反射肩之间，0.68-0.75um之间。

• 非朗伯特性：随着入射光的天顶角的增加，镜面反射增加，偏振度增加。

• 

3.2 植被指数（VIs）及其相关参数关系

• NDVI：归一化植被指数（植被生长状态和植被覆盖）

• RVI：比值植被指数（健康非健康）

• SAVI：土壤修正植被指数（低植被覆盖区）

• DVI：差值植被指数

• EVI：增强植被指数

  • 进一步消除土壤和大气对植被指数的影响，尤其引入蓝光波段，一定程度消除气溶胶、像元破碎卷云的影响

  • 消除背景影响的同时，增强了对浓密植被的敏感性

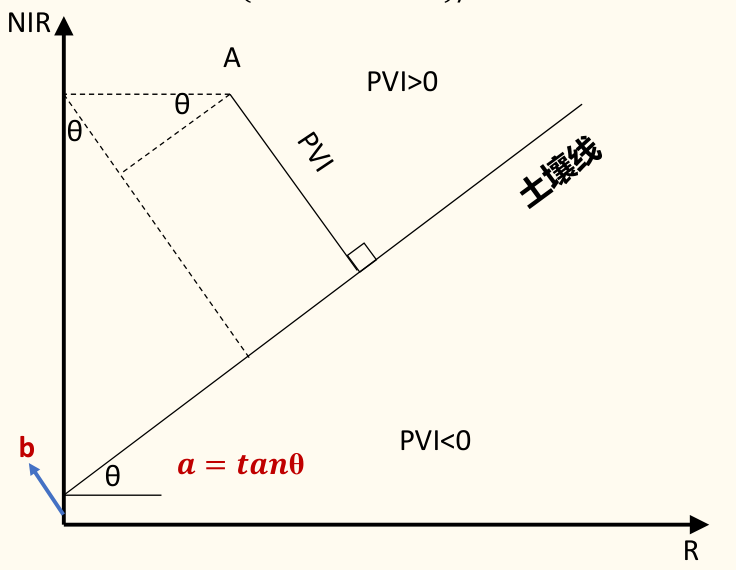
• PVI：垂直植被指数

  • $$
    PVI = \frac{NIR − aR − b}{\sqrt{1 + a^2}}\\ PVI = \frac{NIR \cos\theta− R\sin\theta − b\cos\theta}{\cos^2\theta}
    $$

  • 土壤线：土壤在NIR和R波段反射率具有近似线性关系，表现为一条由近原点的直线

    • $$
      soil = a*R+b
      $$

    • 不同土壤的斜率和截距不同，也不一定完全是线性，而且土壤线通常有一个宽度，精确确定土壤线不容易

  • 植被在土壤线以上，值越大，植被越茂密；其他背景在土壤线及线右下方

  • 

• LAI：单位土地面积上植物叶片单面总面积所占的比例，一般（1，10），LAI越大，光合作用越强，植物干物质累积越多，生物量也就越大，同时反射辐射也增大。

3.3 叶片光学模型

3.3.1 平板模型

• 假定光线是各向同性平行入射，光线在平板内部发生朗伯散射所需的参数

• 将叶片看作N个平板，被N-1个空气间隔分开

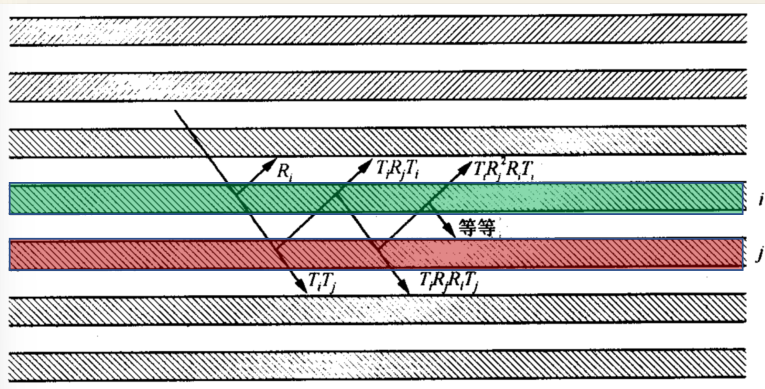
• 单叶辐射传输过程：当第i层和第j层相邻，两层联合反射率

  $$
  R_{ij}=R_{i}+T_{i}R_{j}T_{i}+T_{i}R_{j}^{2}R_{i}T_{i}+T_{i}R_{j}^{2}R_{i}^{2}T_{i}+\cdots=R_i+\frac{T_i^2R_j}{1-R_i R_j}\\T_{ij}=T_{i}T_{j}+T_{i}R_{j}R_{i}T_{j}+T_{i}R_{j}R_{i}R_{j}R_{i}T_{j}+\cdots=\frac{T_i T_j}{1-R_i R_j}
  $$

   

  

• 假如m 层重迭，可以将前m层看成一个整体

  

• 

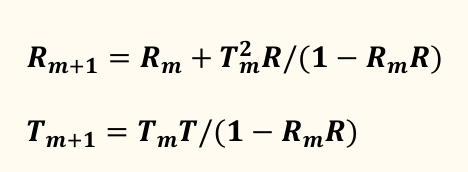
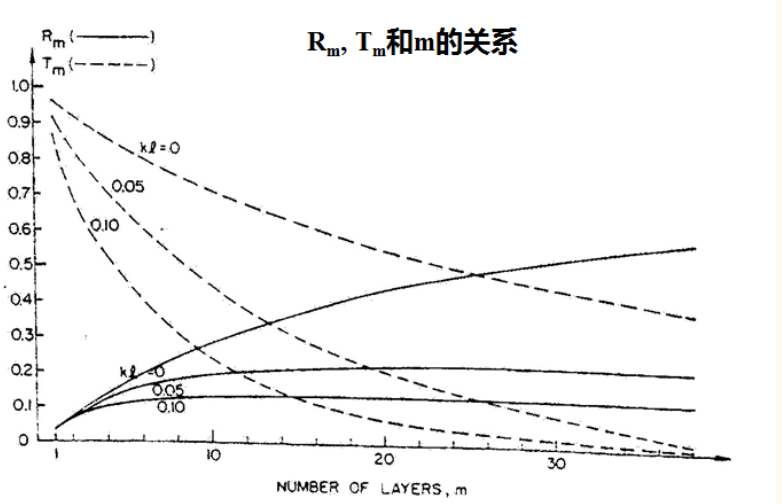
  • 随着m的增长，T_m随之减小而R_m随之增加。光线斜射叶面，相当于光程的增加，亦即m的增加，这就很好地解释了碗边效应的出现

  • 设k为吸收系数，l为薄层厚度，则kl代表该薄层的光学厚度，kl=0相当于近红外波段，叶子对光子吸收很少；当kl = 0.1相当于红色波段的强吸收，反射能量来自表层

  • 内部的散射过程将导致总体的反射率的增加

• 碗边效应：对于均匀介质，在太阳入射的主平面，其反射率会呈现碗边效应，即反射率在星下点最小，随着观测天顶角的增大而增大，呈“碗形”。

3.3.2 PROSPECT模型

• 假定光线都是从这个立体角里穿过叶片的，不再需要入射光线是平行的各向同性光这个假设

• 

3.4 混合像元模型

• 像元反射率是所组成端元（亚像元）的反射率、各端元所占面积比例的函数

• 端元：分解混合像元时，被分解出来的成分

  • 组成混合像元的最基本的单元

  • 每个端元通常对应一种地物

3.5 线性光谱分离模型（LSU）

• n个端元的混合像元在第i个波段的反射率为：

  $$
  R_i = \sum_i^n(\rho_{ij}a_j)
  $$

   

  其中R_i为遥感观测的反射光谱，\rho为端元的反射率，a为端元的面积比例。

• 考虑一个混合像元只有植被(v)和裸土(s)，此时混合像元反射率为：

  $$
  R=\rho_{v}a_{v}+\rho_{s}{(1-a}_{v})
  $$

• 考虑一个混合像元里存在植被、裸土和水体：（构建方程组）

  $$
  R = \rho_Aa_A+\rho_Ba_B+\rho_C(1-a_A-a_B)
  $$

• LSU的精度取决于：遥感反射率、端元反射率、线性假设

3.6 冠层几何光学模型

• 冠层反射率：指植被上界出射辐射与入射辐射的比值

• 主要用来描述宏观物体的方向性反射现象

• 热点效应：当传感器与太阳位于同一方向时，传感器所接收的地面辐射最强（地面反射率最大、地面光强最强、最热）

  • 传感器观测到的不同角度阴影比例不同，阴影逐渐减少，直到看不到阴影

稀疏分布条件

• 遥感像元反射率由四部分组成，即光直接照射的树冠(C)、树冠阴影面(T)、直接照射的地面（背景）(G)、阴影遮蔽的地面(Z)

  $$
  R = K_CR_C+K_TR_T+K_GR_G+K_ZR_Z
  $$

   

  K为该分量在所有像元中所占面积比例

  

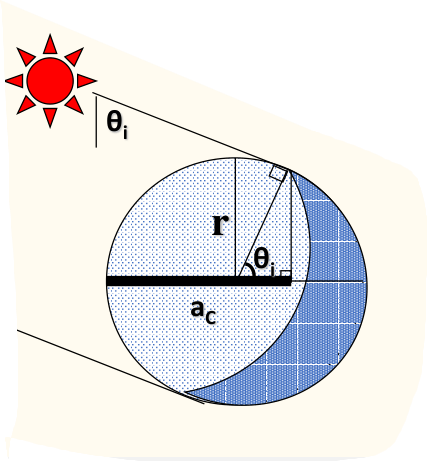
  其中光照树冠面积a_c为传感器垂直下视，太阳以\theta_i的天顶角入射时，球体在垂直方向上的投影（圆心左侧为半圆，圆心右侧为半椭圆）：

  $$
  a_c = \frac{\pi}{2}r^2+\frac{\pi}{2}r\cdot r\cos\theta_i=\frac{\pi}{2}r^{2}(1+\cos\theta_{i})
  $$

   

  阴影树冠面积：

  $$
  a_T = \pi r^2-a_c=\frac{\pi}{2}r^{2}(1-\cos\theta_{i})
  $$

   

  阴影背景面积（太阳光为平行光，阴影为椭圆，短轴不变）：

  $$
  a_z=\pi r\cdot\frac{r}{\cos\theta_i}
  $$

• 假设一个像元内有n棵树，第j颗树的树冠半径为r_j，像元面积为A：

  $$
  A_C = \sum (a_c)_j\\A_T = \sum (a_T)_j\\A_Z = \sum (a_Z)_j\\A_G=A-A_C-A_T-A_Z=A-\pi(1+\sec\theta_i)\sum_{j=1}^nr^2_j
  $$

• 引入统计数据单位面积内树木平均个数\lambda，树冠平均半径为R：

  $$
  \sum_{j=1}^nr^2_j=\lambda A r_0^2\\ \begin{aligned} &{A}_{C} =\lambda A\frac{\pi{r_{0}}^{2}}{2}(1+\cos \theta i) \\ &A_T =\lambda A\frac{\pi{r_0}^2}{2}(1-\cos\theta i) \\ &A_{Z} =\lambda A\pi{r_0}^{2}\sec\theta_i \\ &A_{G} =A-\lambda A\pi{r_{0}}^{2}({1}+\sec\theta_i) \end{aligned}
  $$

   

  其中m = \lambda\pi r_0^2为林木平均郁密度

• 因此球型的四分量混合像元模型公式是：

  $$
  R=\lambda\pi r^{2}_{0}\left[ \frac{1}{2}(1+\cos\theta_{i})R_{C}+\frac{1}{2}(1-\cos\theta_{i})R_{T}+\sec\theta_{i}R_{Z}-(1-\sec\theta_{i})R_{G} \right]+R_{G}
  $$

• 即使像元内部处处是朗伯体，像元整体也可能是非朗伯的

• 任意视角方向下，像元中四分量的面积比例（旋转坐标系，使观测方向变成垂直）：

  旋转后太阳入射角变为太阳入射方向和传感器观测方向的夹角\Theta

  $$
  \cos \Theta = \cos \theta_i \cos\theta_v+\sin\theta_i\sin\theta_v\cos(\varphi_i-\varphi_v)\\a_{C}^{\prime} =\frac{\pi{{r_{0}}^{2}}}{2}(1+\cos\Theta) \\ a_{T}'={\frac{\pi{r_{0}}^{2}}{2}}\left(1-\cos\Theta\right)\\
  $$

   

  考虑到区域面积投影到视线垂直方向的平面上，像元面积比地面实际面积小，像元面积实为A\cos\theta_v于是像元内光照树冠面积比例：

  $$
  K_C= \lambda \frac{\pi r^{2}_{0}}{2}(1+\cos\Theta )\sec\theta v\\K_T= \lambda \frac{\pi r^{2}_{0}}{2}(1-\cos\Theta )\sec\theta v
  $$

• 模型成立的条件：稀疏分布

• 假设地表被观测地物（不仅限于树冠）有一定的几何形状

浓密（连续）分布条件下林冠模型

• 布尔模型：利用概率统计方法推导光照（可记为1）和阴影（可 记为0）出现的概率。

  • 当从传感器方向\Omega(\theta_v,\varphi_v)看浓密树林，若每颗树木在水平背景的平均投影面积为a(\theta_v,\varphi_v)，则看到背景的概率为e^{-\lambda a(\theta_v,\varphi_v)}（间隙概率公式）

  • $$
    K_{C}+K_{T}=1-e^{-\lambda a(\theta_{v},\varphi_{v})}\\K_{G}+K_{Z}=e^{-\lambda a(\theta_{v},\varphi_{v})}
    $$

  • 光照背景面积比例：背景既被阳光照射，又被传感器看到的概率（重叠部分的面积函数与两个方向的天顶角，相对方位角有关）

• 由于以上推导的冠层反射率与冠层上方入射方向和出射方向均有关系，所以这是一个二向反射模型。

冠层辐射传输模型

• 叶面积体密度（FAVD）：某一高度上单位体积内叶片（单面）面积总和，它在空间分布的形式称为叶面积密度分布，单位为米-1

  • 在植被平面平行分布的假设下，可以用u_L(z)表示FAVD，即叶面积体密度只随垂直高度变化而改变，同一层的叶面积密度是均一的

• LAI：地表单位面积上方所有叶子单面面积的总和

  $$
  \int_0^H u_L(z)\,\text{d}z = LAI
  $$

   

  其中z=0为植被上界，z=H为植被下界

• 叶倾角分布：单位立体角内叶面积的比例

• G函数-消光系数：位置z处，所有叶片的法向在传输方向 Ω 上的平均投影。

  • 光路介质对光子的吸收与散射致使光亮度在传播方向上减弱

• \Gamma函数-叶片散射相函数

  • 表示当方向为\Omega'的辐射入射到法向取向为\Omega_L的叶片时，被散射到\Omega方向的比例

  • 植被辐射传输方程中的散射相函数，隐含了单次散射反照率

• 正向过程：辐射传输方程表述了辐射介质中散射和吸收的规律，通过求解辐射传输方程，可以推知植被体内辐射场分布，从而确定传感器所接收的从植被体内出射的辐射信息

• 反演过程：由于植被出射辐射与植被及其下垫面（土壤）的特性有关，因此可以利用传感器接收信息推知植被—土壤体系内相关因子

• 

• 

四、热红外遥感

• 黑体：能够吸收外来的全部辐射，并且不会有任何的反射与透射吸收率为1，反射率和透过率皆为0

• 热红外辐射不仅与物质的表面状态有关，而且是物质内部组成和温度的函数

• 普朗克定律：在一定温度下，单位面积的黑体在单位时间、单位立体角内和单位波长间隔内辐射出的能量为：

  • $$
    M_b(\lambda,T)=\frac{c_{1}\lambda^{-5}}{e^{\frac{c_{2}}{\lambda T}}-1}\\c_{1}=2\pi hc^{2}=3.74\times 10^{-16} Wm^{-2}\\c_2 = \frac{hc}{k}=1.44 \times 10^{-2} mK
    $$

     

    h为普朗克常数，k为玻尔兹曼常数

  • 在给定温度T条件下，从一个黑体中发射出的电磁辐射与波长/频率之间的关系

  • 在给定波长条件下，从一个黑体中发射出的电磁辐射与温度之间的关系

  • 黑体辐射特征：

    • 辐射通量密度随波长连续变化，每条曲线只有一个最大值。

    • 温度愈高，辐射通量密度也愈大，不同温度的曲线是不相交的。

    • 随着温度的升高，辐射最大值所对应的波长移向短波方向。

• 斯蒂芬-玻尔兹曼定律：黑体表面单位面积在单位时间内辐射出的总能量与物体绝对温度 的四次方成正比

  • 推导：普朗克函数在全谱段内的积分，即黑体的总辐射输出射度

• 维恩位移定律：黑体辐射的峰值波长与T的定量关系

  $$
  \lambda_{max} = \frac{b}{T}
  $$

   

  • 推导：普朗克函数对波长求导

• 基尔霍夫定律：物体的比辐射率等于物体的吸收率，即物体的辐射能力越大，吸收能力也越大

• 比辐射率：表征地物发射本领的物理量，又称发射率，指任何物体在温度T和波长\lambda处的辐射出射度与同条件下黑体出射度的比值

  $$
  \varepsilon_{\lambda}=\frac{M(\lambda,T)}{M_{b}(\lambda,T)}
  $$

   

  • 黑体：发射率等于1

  • 灰体：发射率小于1

• 热红外辐射在大气中的传输，是一种漫射辐射在无散射、但有吸收又有发射的介质中的传输。

• 热红外辐射大气传输的一般假设：

  • 地球与大气都是发射红外辐射的辐射源

  • 大气任一平面出射的都是具有各个方向的漫射辐射

  • 只考虑吸收作用，忽略散射

  • 大气的发射和吸收同时考虑

  • 假定大气是水平均一的平面平行大气

• $$
  L=T_{b}= \varepsilon B\left(T_{s}\right) \gamma^{\uparrow}+(1-\varepsilon) L_{a t m}^{\downarrow} \gamma^{\uparrow}+L_{a t m}^{\uparrow}+L_{a t m-s}^{\uparrow}+\rho \mu E_{0} \gamma^{\downarrow} \gamma^{\uparrow} / \pi
  $$

   

  1. 地表的贡献，其中B为普朗克公式计算的发射辐射

  2. 大气向下的热辐射被地表反射的部分

  3. 大气的贡献

  4. 太阳反射波段大气贡献

  5. 太阳光经大气衰减和地表反射后的辐射

• 亮温：辐射出与观测物体相等辐射能量的黑体温度

海洋表面温度反演（SST）

• 方法：分裂窗算法、分窗算法，劈窗算法

• 海水近似为黑体，比辐射率等于1

• 大气窗口的水汽吸收较弱

• 大气温度与海面温度相差不大，普朗克公式可以采用线性近似。

• SST反演一般形式：

• $$
  \begin{array}{l} T_{\mathrm{s}}=T_{\mathrm{b} 1}+\beta\left(T_{\mathrm{b} 1}-T_{\mathrm{b} 2}\right)\\ T_{\mathrm{s}}=T_{\mathrm{b} 1}+\beta\left(T_{\mathrm{b} 1}-T_{\mathrm{b} 2}\right)+\delta\\ T_{\mathrm{s}}=a T_{i}+b T_{j}+c \end{array}
  $$

   

  b1和b2为两个通道，\beta = \frac{1}{\frac{k_1}{k_2}-1}

• 确定系数：

  • 大范围实测海面温度，基于大量数据点对（亮温、SST）利用最小二乘法拟合

  • 设置各种观测、大气条件，基于辐射传输模型计算大量的模拟数据，通过模拟数据进行拟合

地表温度反演（LST）

劈窗算法

• 陆地精度低，反演精度受下面几种因素影响：

  • 陆地表面的比辐射率一般小于1，而且时空变化大(11~12μm、 0.9~0.99)

  • 陆地表面的比辐射率随波长变化

  • 陆地表面的比辐射率随观测角变化

  • 陆地表面温度和近地表气温差远大于海面（普朗克泰勒一级近似误差大）

  • 陆地表面温度在一个像元内变化很大

  • 地表反射的大气向下辐射不可忽略

单窗算法

• Lansat 5/TM：

• 大气顶热辐射信息：

  $$
  B_6(T_6)=[\varepsilon_6B_6(T_s)+(1-\varepsilon_6)R_a^{\downarrow}]\tau_6+R_a^{\uparrow}
  $$

• 推导拟合后：

  $$
  T_s=[a_6(1-C_6-D_6)+b_6(1-C_6-D_6)+C_6+D_6]T_6+D_6T_a/C_6
  $$

   

  其中C_6 = \tau_6 \varepsilon_{6},D_6 =(1-\tau_6)[1+\tau_6(1-\varepsilon_6)] 未知数：发射率\varepsilon_{6}；大气上行透过率\tau_6；大气作用平均温度T_a

• 大气作用平均温度参数化

• 大气透过率参数

• 比辐射率的确定：基于NDVI分割

MODIS Day/Night算法

• 引入中红外通道，减少未知数的个数，满足方程求解条件

• 引入白天和晚上的数据，假定2个时刻地物的比辐射率不变，2个时刻大气会变

• N个波段，两个时刻，2N个方程，其中未知数为：N个发射率，2个LST，2个大气温度，个大气水汽，1个非各项同性角度因子（BDRF相关校正项）

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！