2019/12/06测试

#一次不算难的测试

题1：超氧化钾(mod.cpp)
【题目描述】
作为一个化学小考只有77分的同学，小W感觉很有压力，所以他决定搞化学。今天他开始研究超氧化钾，这是一种很神奇的离子化合物，在高温下空间结构是立方体，如下图所示。

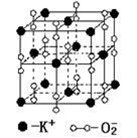
有一天老黄交给了小W一个任务：根据老黄多年研究OI的经验，他发现超氧化钾有一个神奇的性质就是如果一组有序的整数(x,y,z)满足z=x mod 1+x mod 2+…+x mod y，那么对于超氧化钾来说这个位置上的离子就是一个关键离子。通过用回旋加速器得到高速粒子来攻击这个离子，他就可以获得铜铝制金法( 2Cu + 2Al == 2Au + Cl2↑ )的催化剂。现在教黄想知道对于一个给定的x和y对应的z值是多少。
【输入格式】
两个整数x,y。
【输出格式】
一个整数z。
【输入样例】
5 10 29
【输出样例】
29
【数据范围】
对于 40%的数据，n≤ 1 0 5 10^5 105,m≤ 1 0 5 10^5 105 ；
对于 100%的数据，n≤ 1 0 9 10^9 109,m≤ 1 0 9 10^9 109 ；
正解

#include
#include
#define ll long long 
using namespace std;
ll n,k,ans; 
int main()
{freopen("mod.in","r",stdin);freopen("mod.out","w",stdout);fscanf(stdin,"%lld%lld",&k,&n); ans=n*k;for( long long x=1,gx;x<=n;x=gx+1){gx=k/x?min(k/(k/x),n):n; ans-=(k/x)*(x+gx)*(gx-x+1)/2; }fprintf(stdout,"%lld",ans);fclose(stdin);fclose(stdout);
}

Of course,本人不会这么高级的算法：

#include
#include
using namespace std;
int main()
{freopen("mod.in","r",stdin);freopen("mod.out","w",stdout);register int m,n;register long long ans=0;cin>>n>>m;for(register int i=1;i<=m;i++)ans+=n%i;cout<<ans;return 0;
}
//但我还是卡过去了（0.984s）（滑稽

题2:艰难的选择(choice.cpp)
题目描述
近来，初一年的xxx小朋友致力于研究班上同学的配对问题（别想太多，仅是舞伴），通过各种推理和实验，他掌握了大量的实战经验。例如，据他观察，身高相近的人似乎比较合得来。
万圣节来临之际，XXX准备在学校策划一次大型的“非常男女”配对活动。对于这次活动的参与者，XXX有自己独特的选择方式。他希望能选择男女人数相等且身高都很接近的一些人。这种选择方式实现起来很简单。他让学校的所有人按照身高排成一排，然后从中选出连续的若干个人，使得这些人中男女人数相等。为了使活动更热闹，XXX当然希望他能选出的人越多越好。请编写程序告诉他，他最多可以选出多少人来。
【输入格式】
第一行有一个正整数n，代表学校的人数。
第二行有n个用空格隔开的数，这些数只能是0或1，其中，0代表一个女生，1代表一个男生
【输出格式】
输出一个非负整数。这个数表示在输入数据中最长的一段男女人数相等的子序列长度。
如果不存在男女人数相等的子序列，请输出0。
【输入样例】
9
0 1 0 0 0 1 1 0 0
【输出样例】
6
【数据范围】
对于 30%的数据，n≤ 5 ∗ 1 0 3 5*10^3 5∗103；
对于 100%的数据，n≤ 1 0 5 10^5 105；
男为1，女为-1，
跑个前缀和+优化，记录最先出现该数值的点
记得处理负下标
直接A掉

#include
#include
#define N 100001
using namespace std;
int sum[N],p[N<<1];
int main()
{freopen("choice.in","r",stdin);freopen("choice.out","w",stdout);register int n,ans=0;scanf("%d",&n);for(register int i=1,x;i<=n;i++){scanf("%d",&x);sum[i]=sum[i-1];sum[i]+=x?1:-1;if(!p[sum[i]+N])p[sum[i]+N]=i;else ans=max(ans,i-p[sum[i]+N]);}printf("%d",ans);return 0;
} 

题3：改造二叉树(change.cpp)
【题目背景】
勤奋又善于思考的小L接触了信息学竞赛，开始的学习十分顺利。但是，小L对数据结构的掌握实在十分渣渣。
所以，小L当时卡在了二叉树。
【题目描述】
在计算机科学中，二叉树是每个结点最多有两个子结点的有序树。通常子结点被称作“左孩子”和“右孩子”。二叉树被用作二叉搜索树和二叉堆。随后他又和他人讨论起了二叉搜索树。什么是二叉搜索树呢？二叉搜索树首先是一棵二叉树。设key[p]表示结点p上的数值。对于其中的每个结点p，若其存在左孩子lch，则key[p]>key[lch]；若其存在右孩子rch，则key[p] 可是善于思考的小L不甘于只学习这些基础的东西。他思考了这样一个问题：现在给定一棵二叉树，可以任意修改结点的数值。修改一个结点的数值算作一次修改，且这个结点不能再被修改。若要将其变成一棵二叉搜索树，且任意时刻结点的数值必须是整数（可以是负整数或0），所要的最少修改次数。
这一定难不倒聪明的你吧！如果你能帮小L解决这个问题，也许他会把最后的资产分给你1/16哦！
【输入格式】
第一行一个正整数n表示二叉树节点数。
第二行n个正整数用空格分隔开，第i个数ai表示结点i的原始数值。
此后n - 1行每行两个非负整数fa, ch，第i + 2行描述结点i + 1的父亲编号fa，以及父子关系ch，(ch = 0 表示i + 1为左儿子，ch = 1表示i + 1为右儿子)。
为了让你稍微减轻些负担，小L规定：结点1一定是二叉树的根哦！
【输出格式】
仅一行包含一个整数，表示最少的修改次数
【输入样例】
3
2 2 2
1 0
1 1
【输出样例】
2
【数据范围】
对于 40%的数据，n≤$100$,m≤$100$；
对于 60%的数据，n≤$5000$,m≤$5000$；
对于 100%的数据，n≤ 1 0 5 10^5 105,m≤ 1 0 5 10^5 105；

这道题不需要在树上做，因为这题中二叉搜索树的中序遍历是上升序列，只要保证原树的中序遍历修改改后是上升序列即可。
这时我们很容易就想到求最长上升子序列长度，然后得出答案，然后想一想发现这么做不行，
因为不能保证在最长上升子序列的任意相邻两项a[i]和a[j]（设它们分别在原数列的位置位为i,j，原数列为a），都有a[j]-a[i]>=j-i。
解决的办法就是，我们可以把上述的式子移项为a[i]-i<=a[j]-j，那么只要把原数列中每一项a[i]变为a[i]-i，那么问题就变成了求最长不下降子序列的长度的问题。

但 TLE
（我还是再去改改吧）

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！