sdut-array2-4 打印“杨辉三角“ 品中国数学史 增民族自豪感

背景介绍： 北宋人贾宪约1050年首先使用“贾宪三角”进行高次开方运算。

南宋数学家杨辉在《详解九章算法》（1261年）记载并保存了“贾宪三角”，故称杨辉三角。杨辉三角是中国数学史上的一个伟大成就。 杨辉三角，是中国古代数学的杰出研究成果之一，它把二项式系数图形化，把组合数内在的一些代数性质直观地从图形中体现出来，是一种离散型的数与形的结合。

中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现。在欧洲，帕斯卡（1623----1662）在1654年发现这一规律，所以这个表又叫做帕斯卡三角形。帕斯卡的发现比杨辉要迟393年，比贾宪迟600年。

杨辉三角数字的特点为：

（1）在三角形的首列和对角线上，数值均为1；

（2）其余数据为：每个数字等于上一行的左右两个数字之和，第n+1行的第i个数等于第n行的第i-1个数和第i个数之和，用公式表示为： C(n+1,i)=C(n,i)+C(n,i-1)。

图示为：

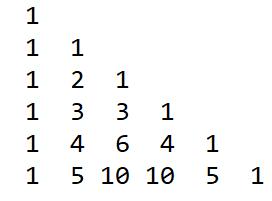
杨辉三角的应用：(a+b)的n次方，展开式中的各项系数依次对应杨辉三角的第(n+1)行中的每一项。

输入格式:

欲打印杨辉三角的行数n（1<=n<=13)。

输出格式:

每个数字占据4个字符的位置，数字左对齐，数字不足4位的右边留出空格。

输入样例:

13

结尾无空行

输出样例:

1   
1   1   
1   2   1   
1   3   3   1   
1   4   6   4   1   
1   5   10  10  5   1   
1   6   15  20  15  6   1   
1   7   21  35  35  21  7   1   
1   8   28  56  70  56  28  8   1   
1   9   36  84  126 126 84  36  9   1   
1   10  45  120 210 252 210 120 45  10  1   
1   11  55  165 330 462 462 330 165 55  11  1   
1   12  66  220 495 792 924 792 495 220 66  12  1

#include
int main()
{int a = 0, s[13][13] = { {0} };scanf("%d", &a);int i = 0, j = 0, k = 0;for (i = 0; i < a; i++){s[i][0] = 1;//每行第一l列的数都为1;}//当三角只有一行时if (a <= 1){for (i = 0; i < a; i++){for (j = 0; j < a; j++){printf("%-4d", s[i][j]);}}}//三角形行数大于2时if (a > 1){//先确定第一二行的数据for (i = 1; i < 2; i++){for (j = 0; j < 2; j++){s[i][j] = 1;}//第一二行元素确定}//输出一二行已经确定的元素printf("%-4d\n", s[0][0]);printf("%-4d", s[1][0]);printf("%-4d\n", s[1][1]);}//计算第三行第二列开始的各元素for (i = 2; i < a; i++){j = 1;//由于每行第一列第一个元素都已经确定是1了,所以直接从第二列开始printf("%-4d", s[i][0]);while (1){s[i][j] = s[i - 1][j] + s[i - 1][j - 1];printf("%-4d", s[i][j]);//保证只输出半个三角形,根据题目三角形形状要求if (j == i){break;}j++;}if (i != a - 1)//为了保证最后一行不换行{printf("\n");}}
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！