牛顿法求解平方根(一种计算机实现开根的方式)
前言
最近看到一个非常有趣的方法,叫做牛顿法,可以用于求解一个数的平方根,当然可以扩展到求实数或复数域。
牛顿法
话不多说直接上图,一目了然。
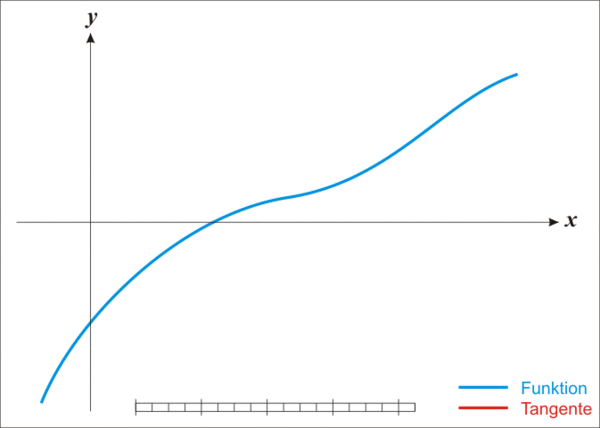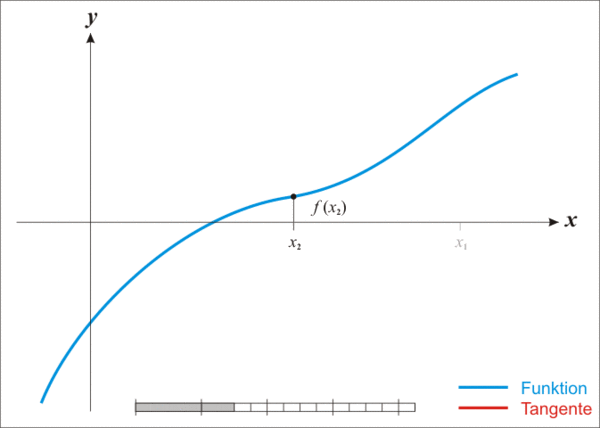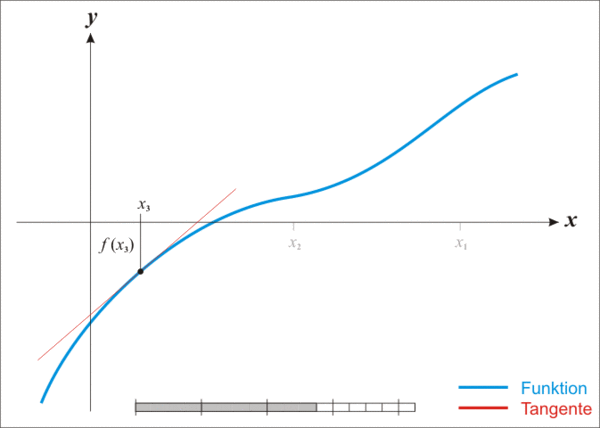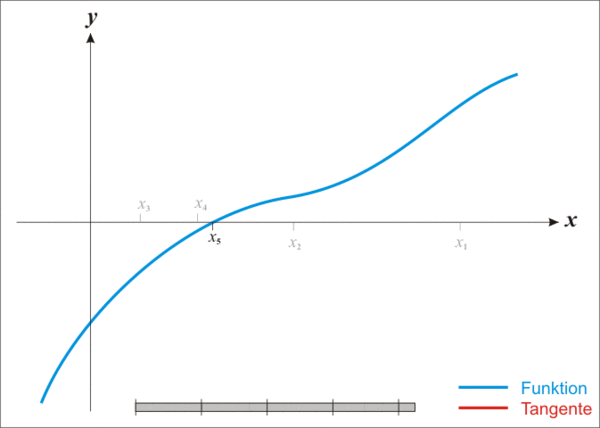
我们先在一个点 x n x_n xn处做切线,然后这条切线与x轴的交点 x n + 1 x_{n+1} xn+1就是我们下一个做切线的位置。
如果是二次函数的话,是很简单的导数运算,切线方程: y = f ′ ( x n ) ( x − x n ) + f ( x n ) y = f'(x_n)(x - x_n) + f(x_n) y=f′(xn)(x−xn)+f(xn),求交点就是把y置为零就可以了。
推导出这个公式-------> x n + 1 = x n − f ( x n ) f ′ ( x n ) x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)} xn+1=xn−f′(xn)f(xn)!!
看图就会发现离真实的解越来越近了,多次迭代就可以得出近似值,是不是很简单?
不过牛顿法还是有限制的:
- 需要区间内 f ′ ( x ) f'(x) f′(x)≠0,不然无法求交点
- 在x求解区间内, f ′ ′ ( x ) f''(x) f′′(x)是连续的
Go代码
语言大同小异,其实还是比较容易看懂的,就是循环了十次,当然次数越多越逼近啊!
func Sqrt(x float64) float64 {z := 1.0for i := 1; i <= 10; i++ {z -= (z*z - x) / (2*z)}return z
}
x是目标值,z是目标值的平方根需要被求解。
所求函数是 f ( z , x ) = z 2 − x f(z,x)=z^2-x f(z,x)=z2−x,对z求偏导 ∂ f ( z , x ) ∂ z = 2 z \frac{\partial f(z,x)}{\partial z}=2z ∂z∂f(z,x)=2z。
代入 x n + 1 = x n − f ( x n ) f ′ ( x n ) x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)} xn+1=xn−f′(xn)f(xn)就是中间循环的内容z -= (z*z - x) / (2*z)。
参考链接:
- https://zh.wikipedia.org/wiki/牛顿法
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!