机器人运动学标定：基于公垂线模型的指数积标定——减少标定参数，避免过度约束

文章目录

• 基于旋量理论的公垂线变换研究——用公垂线思考误差模型的前提
• 基于公垂线模型的六轴串联工业机器人实际正向运动学建模
• 基于公垂线模型的误差建模分析及参数辨识
• 本文使用的指数映射关于旋量微分求解公式
• 对正运动学公式进行全微分线性化并选择误差参数，建立误差参数辨识模型
• 基于迭代最小二乘法的误差参数辨识
• 参考文献

基于旋量理论的公垂线变换研究——用公垂线思考误差模型的前提

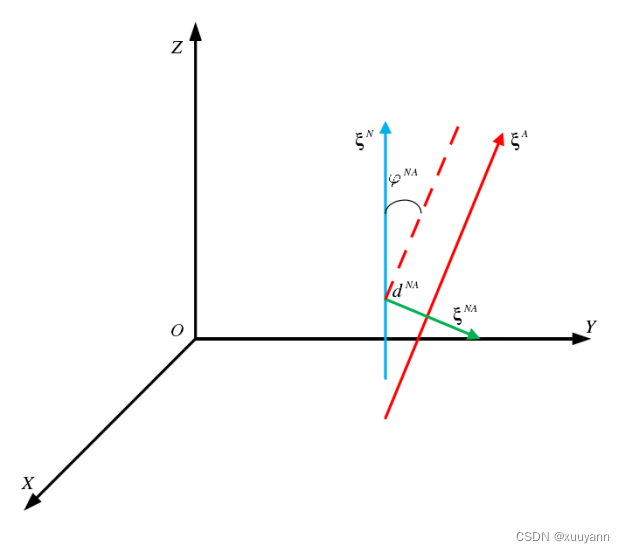
基于公垂线模型的六轴串联工业机器人实际正向运动学建模

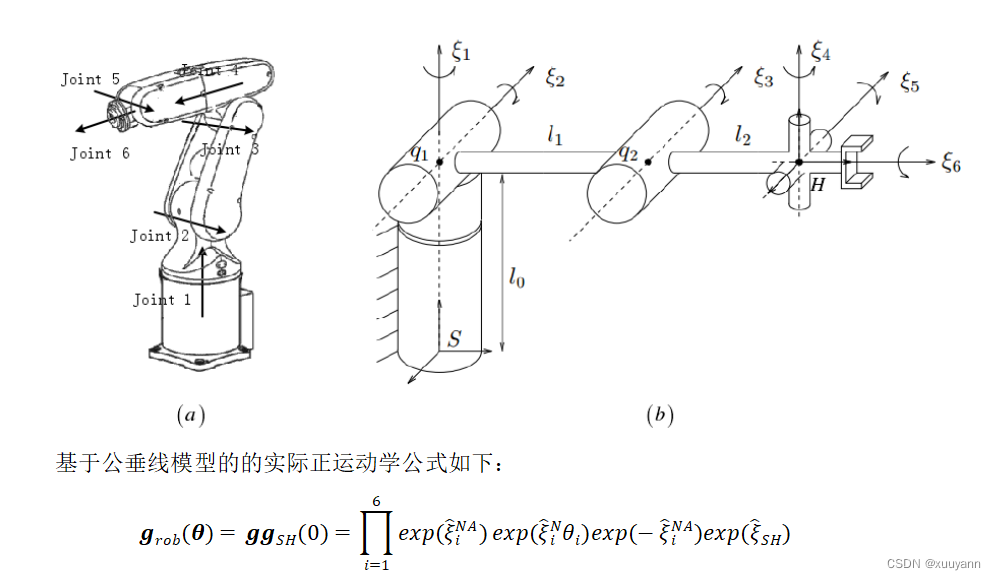
基于公垂线模型的误差建模分析及参数辨识

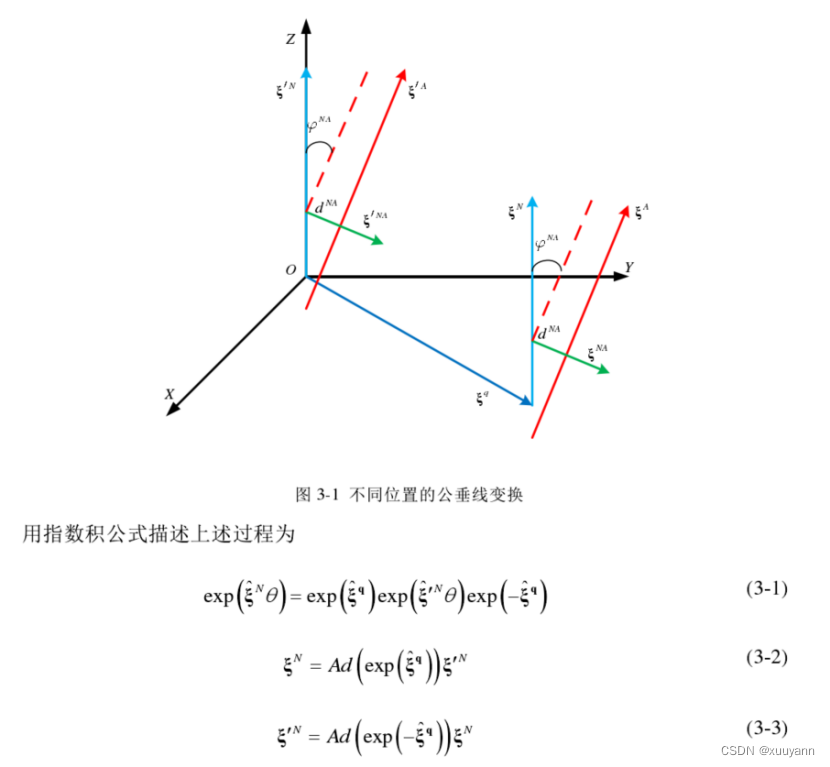
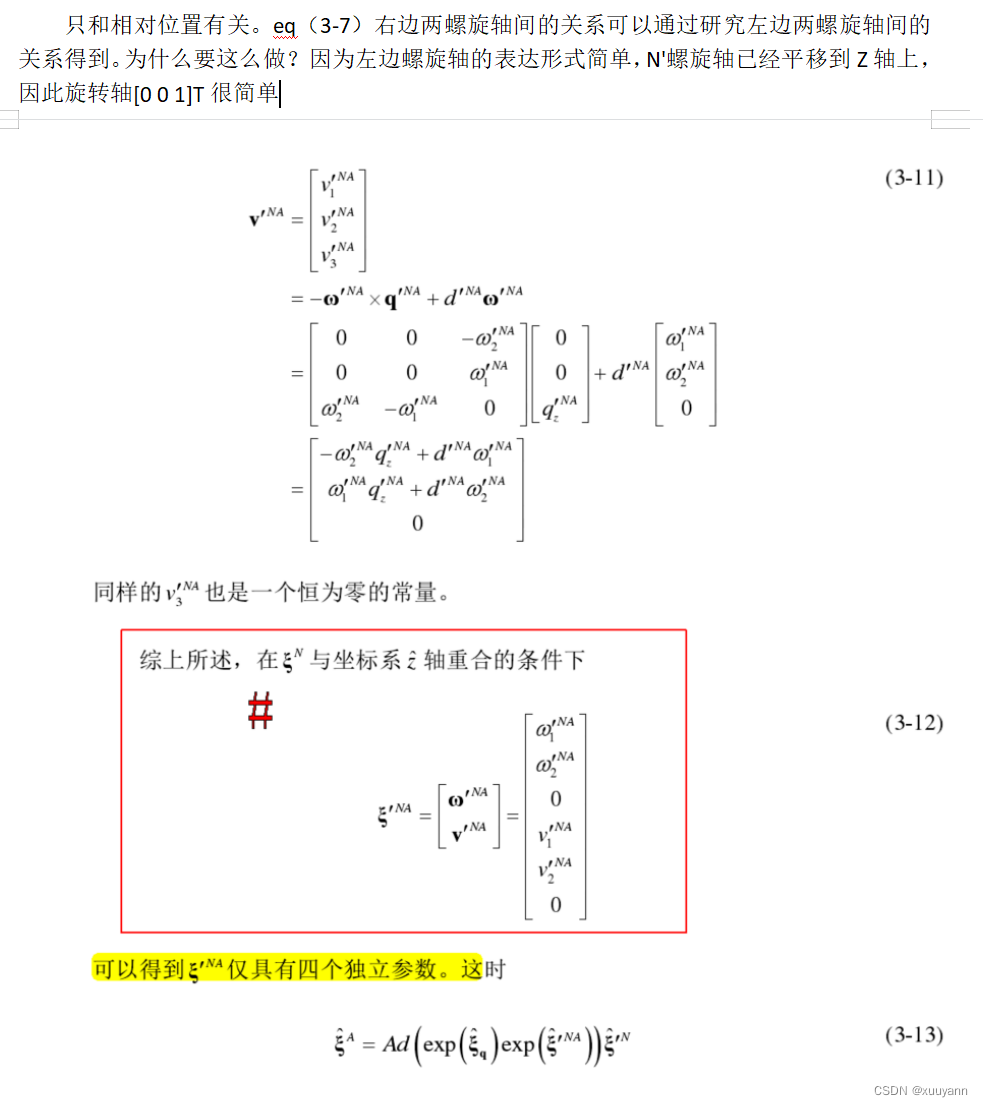
本文使用的指数映射关于旋量微分求解公式

对正运动学公式进行全微分线性化并选择误差参数，建立误差参数辨识模型

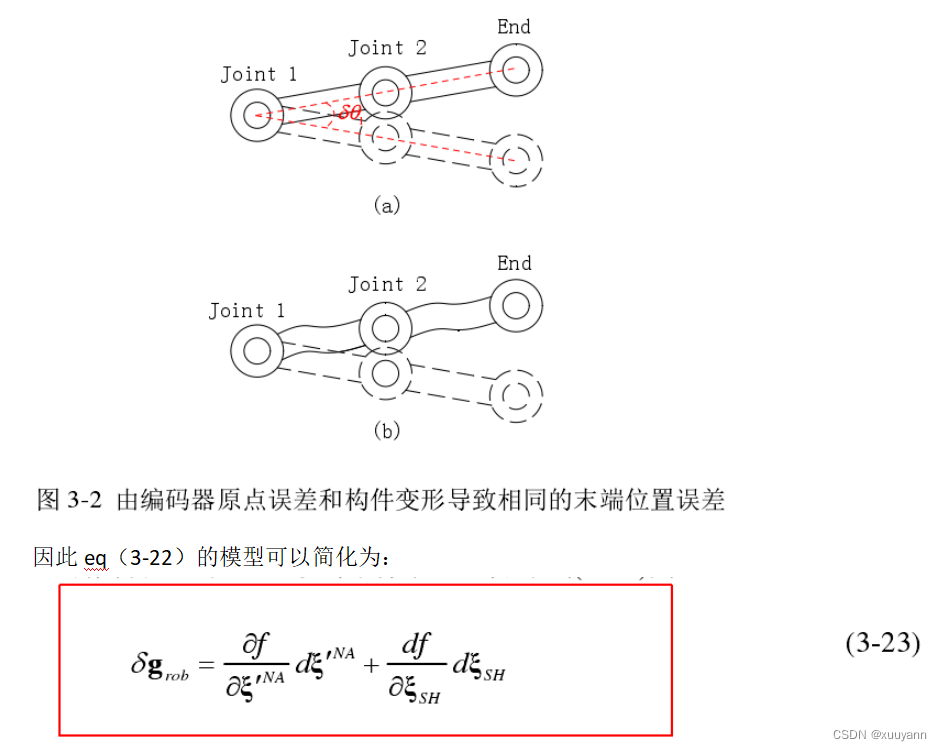
基于迭代最小二乘法的误差参数辨识

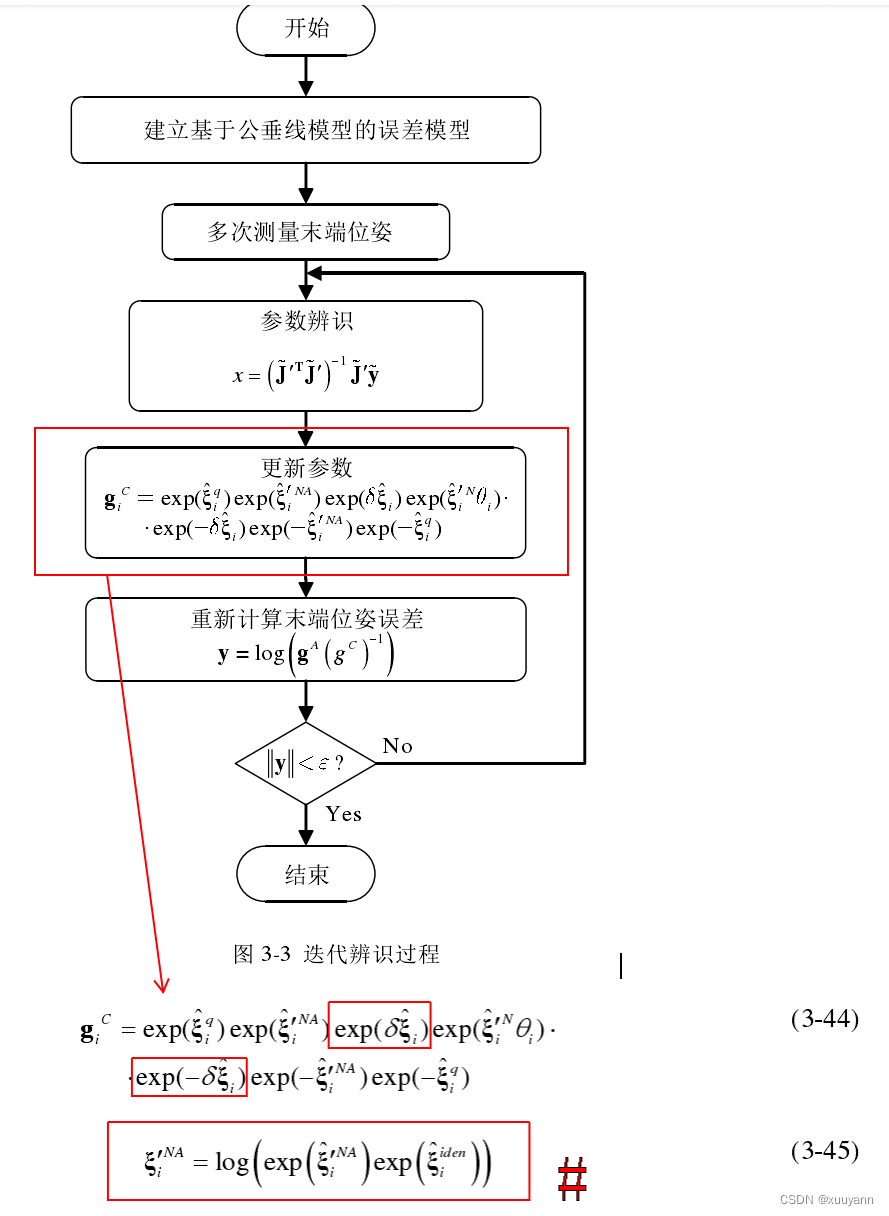
参考文献

[1] 乔昱. 基于公垂线模型的串联机构运动学标定方法研究[D].华中科技大学,2017.
[2] 何锐波. 基于指数积公式的串联机构运动学标定方法研究[D].华中科技大学,2010.
[3] He R, Zhao Y, Yang S, et al. Kinematic-parameter identification for serial-robot calibration based on POE formula[J]. IEEE Transactions on Robotics, 2010, 26(3): 411-423.
[4] Yang X, Wu L, Li J, et al. A minimal kinematic model for serial robot calibration using POE formula[J]. Robotics and Computer-Integrated Manufacturing, 2014, 30(3): 326-334.
[5] 戴建生. 机构学与机器人学的几何基础与旋量代数[M]. 北京:高等教育出版社, 2014.

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！